14.無限長線路の電圧電流分布

前ページ

無限長線路の見え方

開放端線路の例を見ていると、伝送路損失が大となることで終端の状況が無関係に見えてきました。

その究極形態は無限長線路です。そこへのアプローチはいくつか考えられますが、既に開放端線路の結果が十分に揃ったのでその極限をとってやるのが楽そうです。

先に導いたとおり、入力電圧 \(E_1\) を基準とした開放端線路の電圧積分定数は以下のようなものでした。

\begin{eqnarray} V_1 &=& \frac{E_1}{1+e^{-2 \alpha l}} \tag{11.7} \\ V_2 &=& \frac{E_1}{ 1 + e^{2 \alpha l}} \tag{11.8} \end{eqnarray}
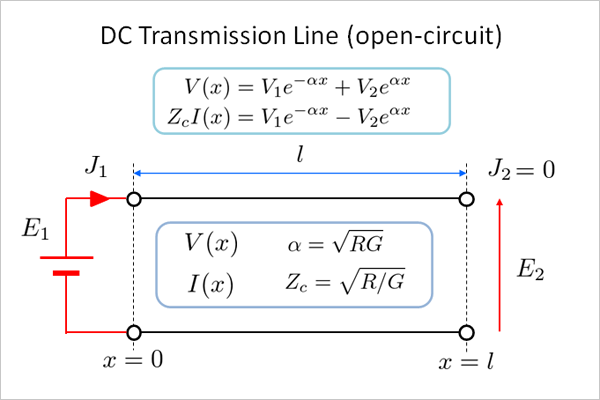
DC Transmission Line (Open-circut)

fig14.1 長さ l の開放端線路（電圧印加）

これら \(V1,V2\) は既に線路長 \(l\) の関数になっているので、そのまま極限を取ることが可能。まずは \(V_1\) からスタート。

\begin{eqnarray} \lim_{l \to \infty} V_1 &=& \lim_{l \to \infty} \frac{E_1}{1+e^{-2 \alpha l}} \\ &=& \frac{E_1}{1+0} \\ &=& E_1 \tag{14.1} \end{eqnarray}

つまり、積分定数 \(V_1\) は電池電圧 \(E_1\) そのものに一致します。開放端の電圧解はV1,V2の線形結合で表現されていたものが、片方の項があっさり消滅してくれます。

V2は既に勝敗が決しているものの、一応考えてみましょう。距離 x=0m （始点）では \[ E_1 = V_1 + V_2 \tag{11.1} \] が成立していることから \( V_2 = 0\) であることも明白（ドヤ！）なのですね。 結果、開放端電圧分布の式(11.9)は第1項のみの簡素な式(14.2)にたどり着きました。 \[ V(x) = E_1 e^{-\alpha x} \tag{14.2} \] 電流分布式にもその論理を適用するならば \[ I_2 = - \frac{V_2}{Z_c} \tag{10.8} \] の関係から、第2項の \(I_2\) も ゼロとなりこちらも式(14.3)へ簡素化できます。 \[ I(x) = \frac{E_1}{Z_c} e^{-\alpha x} \tag{14.3} \]

電圧電流分布の第2項 \(\exp (\alpha x) \) は始端から離れるほど増大する項＝終端反射影響項とみなせることは先に述べました。 無限長では終端の存在自体が抹殺されているので、この結果は当然といえば当然なのです。（屁理屈を言えば、ここらの話は半無限長とかいう分類なんですが無視しましょう。）

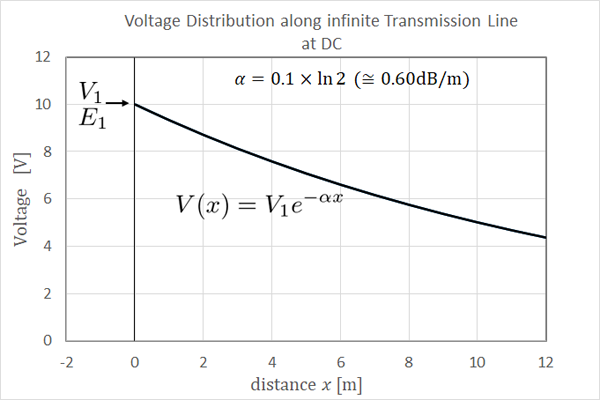
Voltage Distribution along infinite Transmission Line at DC

fig14.2 無限長線路の電圧分布

電流分布グラフも全く同じで、縦軸の単位がアンペアになるだけなので省略します。そして、始端から見た入力インピーダンスは \[ Z_1|_{l=\infty} = Z_c \tag{14.4} \] 。すなわち、無限長線路の入力インピーダンスは特性インピーダンスとなることも明らかなのでした。

無限長線路の擬似回路

無限長は実在しませんが、現実世界でも線路損失が大であれば同一特性を示すことは先に述べました。

ここで思考実験。特性Z が \(Z_c\) の無限長線路を用意します。そして距離 \(x=l\) でばちこんと切断するときの特性はどうなるでしょうか。

入力側から見れば長さ \( l \) の開放端線路特性になるのは当たり前。では切断した残りの部分はどうなるか？普通に考えるならそれも無限長線路です。さすれば、その切断点から見た入力インピーダンスは \(Z_c\) とならざるを得ません。

ここでインチキ。有限長線路の終端に \(Z_c \) の抵抗器を付けたとします。このとき入力側から見たとき 「線路が無限に続いている」 or 「抵抗が途中に接続されている」 のどちらでしょうか。 そう、それを知ることは不可能なのです。

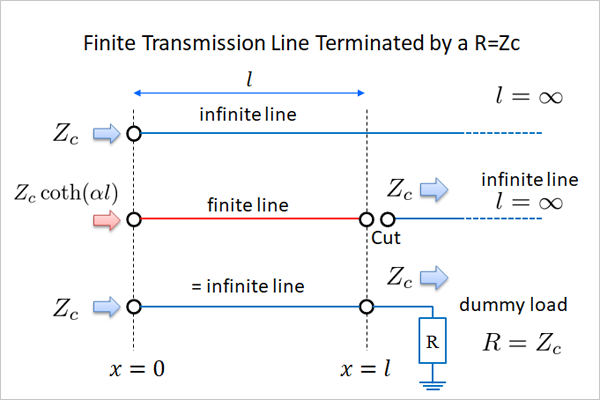
Finite Transmission Line Terminated by a R=Zc

fig14.3 疑似無限長線路と

つまり、無限長線路が示す物理量は単なる1本の抵抗器と変わりないのです。 線路の特性インピーダンスと同じ抵抗をつないだ有限長線路は、常に無限長線路と同等の電圧電流特性になります。 実際の回路でもこの考え方が基本であって、終端抵抗 (terminator) や疑似負荷 (dummy load) と呼ばれており交流信号伝送の反射抑制に使われます。

ここで考えている直流であっても、その考えは成立しているわけです。次は真逆の条件、短絡線路の特性を導いてきます。（作成中）

次ページへ続く