13.開放端伝送線路の線路長影響

前ページ

開放線路の入力インピーダンスと線路長

開放端の線路では終端で電圧が +100% 反射、電流が -100% 反射と考えることで合理的な計算ができそうでした。

とはいえ、実在の線路においては途中の電圧・電流を知りたいことが割合に少ない。そもそも測定できないのが普通でもあって、気になるのは入出力端子の状態だけだったりします。

しからば、線路の長さによって入出力特性がどう変化するかが興味の中心です。ここでは入力インピーダンスを見ていきます。

先の条件を整理すると 始端に電圧源で \(V(0)=E_1\) に固定、終端開放で長さ \(l\) の場所にて電流ゼロ、つまり \(I(l)=J_2=0\) が数式的な表現でした。

電流分布は
\begin{eqnarray} I(x) &=& I_1 e^{-\alpha x} + I_2 e^{\alpha l} \\ &=& \frac{E_1}{Z_c} \left( V_1 e^{-\alpha x} - V_2 e^{\alpha l}\right)\\ &=& \frac{E_1}{Z_c} \left(\frac{e^{-\alpha x}}{1+e^{-2 \alpha l}} - \frac{e^{\alpha x}}{ 1 + e^{2 \alpha l}} \right) \end{eqnarray}
であり、始端の電流 \(J_1\) は p.11 で求めた \[ J_1 = \frac{E_1}{Z_c} \tanh(\alpha l) \tag{11.11} \] でありました。結果、入力インピーダンス \(Z_1\) は
\[ Z_1 = \frac{E_1}{J_1} = \frac{Z_c}{\tanh(\alpha l)} \tag{11.12} \]
でした。

式(11.12)に前ページと同一条件で、線路長 \(l \mathrm{[m]}\) が変化したときの 入力 Z の 変化を描いたものが fig13.1 です。

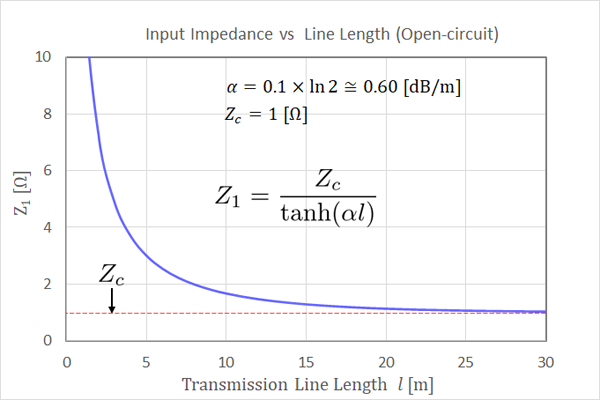
Input Impedance vs Transmission Line Length at DC (Open-circut)

fig13.1 開放線路の入力インピーダンスと線路長

線路長が長くなるにつれて、入力抵抗 \(Z_1\) は 特性インピーダンス \(Z_c\) に収束していく様子がよく分かります。

もしも線路が超短くて 1cm だったときのことを考えてみましょう。 1cm 先で線路が途切れているので高抵抗になるのは容易に想像できます。実際に計算してみると 1.44 kΩ になります。0.1 mm なら 144kΩ ですね。 もちろん線路長 0 は定義できないです。

逆に線路が長大になったとき具体値を挙げれば、26.8m を超えると 1.05Ω でほとんど特性インピーダンスの 1Ω と誤差程度しか差異がありません。\(\alpha l \geq 3\) で 1.32Ω 、 \(\alpha l \geq 5\) で 1.02Ω 。いよいよ見分けが困難になっていきます。

つまり、トータルの線路損失がある程度以上になると終端の状態は意味を失っていくのですね。

なお、tanh関数は素直な関数でもあり、 \[ \lim_{x \to \infty} \tanh (x) = 1 \] と、引数が正の実数である限り、どんな数を入力しようとも 0 から 1 までの間に収まる関数です。(-∞～+∞が -1 ～ +1 に圧縮されるイメージ。)

x が 2 を超えるとほぼ 1 なので、それとの差を ε とすれば \[ \epsilon = 1 - \tanh(x) \simeq 2 e^{-2x} \] という近似式が使えます。

おおむね、線路の総Loss が 17dB (αl=2) を超えると あまり終端の状態が関係なくなってくるイメージで捉えてください。

次はこの極限、無限長での電圧電流分布状況を見ていきます。

次ページへ続く