11.開放線路の解き方と状態
開放線路
ここからは、これまでに得られた式から、両端(境界)条件を与えて伝送路の状態を求めていきます。
伝送路の状態とは、両端子の電圧・電流とそれらの伝送路内分布のことです。このページでは片端を開放して電源を接続した条件で解いてみます。
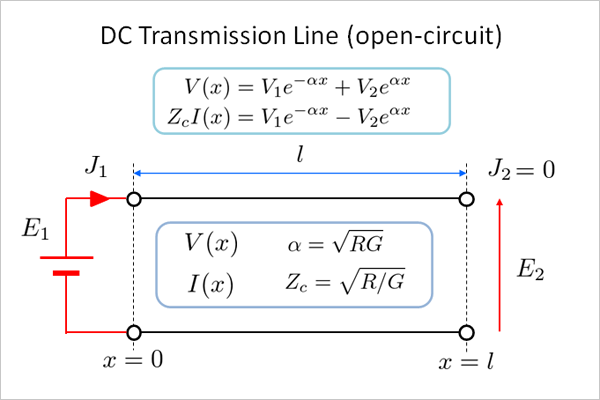
fig11.1 開放線路(電圧印加)
まずは記号の整理から。 \(V,I\) は伝送路内の電圧,電流を。\(E,J\) は端子の電圧,電流を表すこととします。 1次元座標 \(x\) は x=0 を始端とし,伝送路長を \(l\) として x=l を終端とします。
各記号は以下の通りです
- \(E_1\)
- 入力端子電圧(始端)
- \(E_2\)
- 出力端子電圧(終端)
- \(J_1\)
- 入力端子電流(始端)
- \(J_2\)
- 出力端子電流(終端)
- \(Z_1\)
- 入力インピーダンス(始端)
- \(l\)
- 伝送路長 (transmission line Length)
とにかく解いてみる
エレガントな解法はさておき、まずは薩摩示現流でチェストしてみます。
電池(理想電圧源)を始端に接続しているので電圧は \(E_1\) に固定されてます。そして、入力端の座標 \(x=0\) の電圧は
\[
V(0) = V_1 e^{0} + V_2 e^{0} = V_1 + V_2
\]
と簡単に計算できるので、電圧積分定数と印加電圧の関係は
\[
E_1 = V_1 + V_2 \tag{11.1}
\]
とシンプルに求められます。
次に、与えられた境界条件を素直に解釈すると終端開放(Open)なので終端電流は流れません、よって
\[
J_2 = 0 \tag{11.2}
\]
。
この電流条件を方程式に反映させるには、式(10.4)を流用し、
\[
I(l) = J_2 = 0
\]
を代入することで、
\[
\frac{1}{Z_c} \left( V_1 e^{-\alpha l} - V_2 e^{\alpha l} \right) = 0 \tag{11.3}
\]
という関係も得られました。式(11.3)から \(V_1,V_2\)の関係が解明できます。
\[
V_1 e^{-\alpha l} = V_2 e^{\alpha l} \tag{11.4}
\]
ということですから、V2はV1で表現できて
\[
V_2 = V_1 e^{- 2 \alpha l} \tag{11.5}
\]
.
これを式(11.1)に代入してやれば、
\begin{eqnarray}
E_1 &=& V_1 + V_2 \\
&=& V_1 ( 1 + e^{-2\alpha l}) \tag{11.6}
\end{eqnarray}
すなわち、
\[
V_1 = \frac{E_1}{1+e^{-2 \alpha l}} \tag{11.7}
\]
そして、式(11.7)と(11.5)を利用して
\begin{eqnarray}
V_2 &=& V_1 e^{- 2 \alpha l} \\
&=& \frac{E_1 e^{- 2 \alpha l}}{1+e^{-2 \alpha l}} \\
&=& \frac{E_1}{ 1 + e^{2 \alpha l}} \tag{11.8}
\end{eqnarray}
の結果が求められました。
ここでようやく、電圧の積分定数2つが解けたことになります。
最終的に求められた伝送路の電圧分布関数V(x)は
\[
V(x) =E_1 \left(\frac{e^{-\alpha x}}{1+e^{-2 \alpha l}} + \frac{e^{\alpha x}}{ 1 + e^{2 \alpha l}} \right) \tag{11.9}
\]
となりました!
・・・でいいのか、こんな複雑なので。とはいえ、入出力端に限れば、このまま進めても分かりやすい関数で整理できるのである。。。
(実は…頑張るとこんな感じになるのは秘密)
\[
V(x)|_{\mathrm{open}} =E_1 \Bigl( \cosh(\alpha x) - \tanh (\alpha l ) \sinh (\alpha x) \Bigr) \tag{11.9.2}
\]
開放線路の終端電圧、始端電流、インピーダンス
何とか電圧分布が求められましたので、ここからは残る各量を計算していきます。
最初に開放中の終端電圧 \(E_2\) を求めてみましょう。単純に式(11.9)へ \(x=l\) を代入すれば求まります。
\begin{eqnarray}
E_2 &=& V(l)\\
&=& E_1 \left(\frac{e^{-\alpha l}}{1+e^{-2 \alpha l}} + \frac{e^{\alpha l}}{ 1 + e^{2 \alpha l}} \right) \\
&=& E_1 \left(\frac{1}{e^{\alpha l} + e^{-\alpha l}} + \frac{1}{ e^{\alpha l} + e^{- \alpha l}} \right) \\
&=& E_1 \left(\frac{2}{e^{\alpha l} + e^{-\alpha l}} \right) \\
&=& \frac{E_1}{\cosh(\alpha l)}
\end{eqnarray}
結果を抜き出せば
\[
E_2 = \frac{E_1}{\cosh(\alpha l)} \tag{11.10}
\]
と、双曲線関数1つで表せました。やる気があれば \(E_1 \ \mathrm{sech}(\alpha l)\) とも表現できますが、Latex/MathJaxですらサポートしてないマイナー関数なので好きじゃないです。
次に始端電流 \(J_1\) を求めます。ここでは式(10.4)を利用します。
\[
I(x) = \frac{1}{Z_c} \left( V_1 e^{-\alpha x} - V_2 e^{\alpha x} \right) \tag{10.4}
\]
上の式に \(x=0\) を代入すればいいだけなので、
\begin{eqnarray}
J_1 &=& I(0)\\
&=& \frac{1}{Z_c} \left( V_1 - V_2 \right) \\
&=& \frac{E_1}{Z_c} \left( \frac{e^{-\alpha l}}{1+e^{-2 \alpha l}} - \frac{e^{\alpha l}}{ 1 + e^{2 \alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left( \frac{e^{\alpha l} - e^{-\alpha l}}{e^{\alpha l} + e^{-\alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \tanh(\alpha l)
\end{eqnarray}
すなわち、
\[
J_1 = \frac{E_1}{Z_c} \tanh(\alpha l) \tag{11.11}
\]
残るは電池側から見た入力インピーダンス \(Z_1\) で、ここまで来れば簡単に求まります
\[
Z_1 = \frac{E_1}{J_1} = \frac{Z_c}{\tanh(\alpha l)} = Z_c \coth (\alpha l)\tag{11.12}
\]
とりあえず、気合で必要そうな量は全て計算できました。 残るは電流分布とか、あるいは終端側から見たときの線路インピーダンスぐらいでしょう。
電流分布は式(11.9)の結果を式(10.4)に改造してしまえばすぐ求まりますので、ここでは省略します。
このページで計算した結果は単なる数式なので、電流・電圧の分布という物理イメージに結びつきにくいところですので、次ページでは、その振る舞いを見ていこうと思います。
次ページへ続く
