15.短絡線路の解
短絡線路の解き方
ここまで見てきた線路条件は、終端開放と無限長の2条件でした。ここではもう一つの重要な解である短絡線路を扱っていきます。
fig.15.1 はその条件を描いたものです。 電源条件は電圧 \( E_1 \) 印加で前と同じですが、終端をショートしたことにより 終端電流 \(J_2\) はゼロでなくなりました。
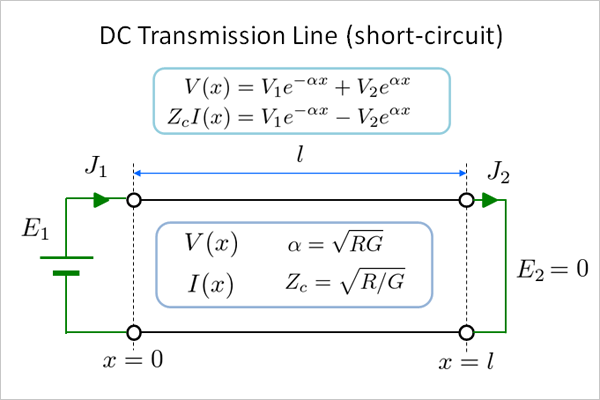
fig15.1 短絡線路(電圧印加)
それに代わる条件は \( E_2 = 0 \) です。短絡によって終端は常に 0V へ固定されることになり、開放時の電流 0A 固定と対照的です。次に方程式と条件を再掲します。
\begin{eqnarray}
V(x) &=& V_1 e^{-\alpha x} + V_2 e^{\alpha x} \tag{9.3} \\
Z_c I(x) &=& V_1 e^{-\alpha x} - V_2 e^{\alpha x} \tag{10.4} \\
V(0) &=& E_1 \tag{15.1} \\
V(l) &=& E_2 = 0 \tag{15.2}
\end{eqnarray}
まず、 式(15.1)の条件を式(9.3)に代入して
\[
V(0) = E_1 = V_1 + V_2 \tag{15.3}
\]
が成立します。同様に 式(15.2)の条件から式(9.3)に代入して
\[
V_1 e^{-\alpha l} + V_2 e ^{\alpha l} = 0 \tag{15.4}
\]
式(15.4)から \(V_1,V_2\) の関係が得られて
\[
V_2 = - V_1 e^{-2 \alpha l} \tag{15.5}
\]
これを 式(15.4) に代入することで,ようやく電圧積分定数 V1 と 入力電圧 E1 の関係を解くことができました。
\[
V_1 = \frac{E_1}{1 - e^{-2 \alpha l}} \tag{15.6}
\]
さらに、式(15.6) と式(15.5)から電圧積分定数V2も容易に解くことができて、その計算を以下のように進めます。
\begin{eqnarray}
V_2 &=& - \frac{E_1}{1 - e^{-2 \alpha l}} e^{-2 \alpha l} \\
&=& - \frac{E_1}{e^{-2 \alpha l}-1} \\
&=& - \frac{E_1}{1-e^{2 \alpha l}} \tag{15.7}
\end{eqnarray}
以上をまとめて、
\begin{eqnarray}
V_1 &=& \frac{E_1}{1 - e^{-2 \alpha l}} \tag{15.6} \\
V_2 &=& \frac{E_1}{1-e^{2 \alpha l}} \tag{15.7}
\end{eqnarray}
これで2つの電圧積分定数 V1,V2 を定めることができました。あとは未知数となっている入力電流 J1 と 短絡側電流 J2 をそれぞれ求めていくだけです。
短絡側の電流を求める
式(10.4) の電流分布式に 電圧積分定数 式(15.6) と 式(15.7) を代入して計算を進めます。まずは出力電流 \(J2=I(l)\) を求めましょう
\begin{eqnarray}
J_2 &=& \frac{1}{Z_c} \left(V_1 e^{-\alpha l} - V_2 e^{\alpha l} \right) \\
&=& \frac{1}{Z_c} \left( \frac{E_1}{1 - e^{-2 \alpha l}} e^{-\alpha l} - \frac{E_1}{1-e^{2 \alpha l}} e^{\alpha l} \right) \\
&=& \frac{E_1}{Z_c} \left( \frac{e^{-\alpha l}}{1 - e^{-2 \alpha l}} - \frac{e^{\alpha l}}{1-e^{2 \alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left( \frac{1}{e^{\alpha l} -e^{-\alpha l}} - \frac{1}{e^{-\alpha l} -e^{\alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left( \frac{1}{e^{\alpha l} -e^{-\alpha l}} + \frac{1}{e^{\alpha l} -e^{-\alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left( \frac{2}{e^{\alpha l} -e^{-\alpha l}} \right) \\
&=& \frac{E_1}{Z_c \sinh(\alpha l)}
\end{eqnarray}
ちょっと丁寧な長い計算でしたが、結果だけをまとめて
\[
J_2 = \frac{E_1}{Z_c \sinh(\alpha l)} \tag{15.8}
\]
これが短絡線に流れる出力電流です。またまた双曲線関数ひとつで表現できてますね。
入力電流と入力インピーダンスを求める
入力電流 \(J_1\) を求めるには、式(10.4) の電流分布式を \(x=0\) とした上で、電圧積分定数 (式(15.6),式(15.7)) を代入すれば求まります。
\begin{eqnarray}
J_1 &=& \frac{1}{Z_c} \left(V_1 - V_2 \right) \\
&=& \frac{1}{Z_c} \left(\frac{E_1}{1 - e^{-2 \alpha l}} - \frac{E_1}{1-e^{2 \alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left(\frac{1}{1 - e^{-2 \alpha l}} - \frac{1}{1-e^{2 \alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left(\frac{e^{\alpha l}}{e^{\alpha l} - e^{-\alpha l}} - \frac{e^{-\alpha l}}{e^{-\alpha l} - e^{\alpha l}} \right) \\
&=& \frac{E_1}{Z_c} \left(\frac {e^{\alpha l} + e^{-\alpha l}}{e^{\alpha l} - e^{-\alpha l}} \right) \\
&=& \frac{E_1}{Z_c \tanh(\alpha l)}
\end{eqnarray}
またまた長い計算でしたが、結果をまとめて
\[
J_1 = \frac{E_1}{Z_c \tanh(\alpha l)} \tag{15.9}
\]
面白いことに、こちらの入力電流も双曲線関数になっています。
入力インピーダンス \(Z_1\) は入力電圧 \(E_1\) と 入力電流 \(J_1\) の比をとればいいだけですから、
\[
Z_1 = \frac{E_1}{J_1} = Z_c \tanh(\alpha l) \tag{15.10}
\]
とカンタンに求められます。
ここまでで得られた解は次ページで具体値を見ていきましょう。
次ページへ続く
