12.開放端伝送線路(DC)の具体的な電圧電流分布

前ページ

開放線路の電圧分布状態

ここまでで得られた開放端線路のDC電圧・DC電流状況は数式のみでしたので、現実のイメージが湧かないですね。

ですので、ここでは図表も交えてより具体的な分布イメージを説明していきたいと思います。

まずは電圧分布式(11.9)を、再掲しておきます。

\[ V(x) =E_1 \left(\frac{e^{-\alpha x}}{1+e^{-2 \alpha l}} + \frac{e^{\alpha x}}{ 1 + e^{2 \alpha l}} \right) \tag{11.9} \]
そこで得られた終端側の開放電圧\(E_2\)は \[ E_2 = \frac{E_1}{\cosh(\alpha l)} \tag{11.10} \] でしたし、始端側の電圧は電池電圧 \(E_1\) そのものなので、これは置いときます。

では、実際に終端開放線路の具体的な電圧分布図を描いてみましょう。電池電圧（電圧源）は \(E_1 = 10\mathrm{V}\) にします。

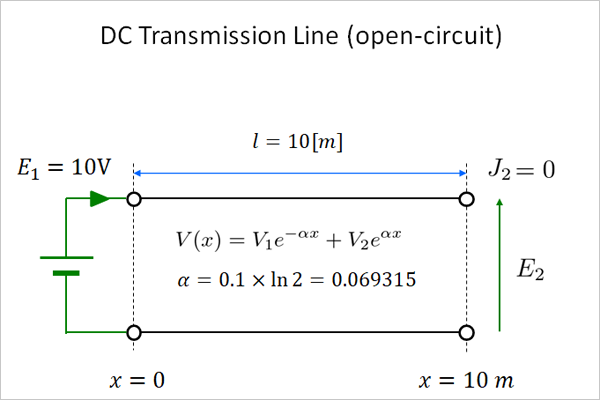
DC Transmission Line at DC (Open-circut)

fig12.1 開放線路への電圧印加状況

その他のパラメータも分かりやすいように \(\alpha = 0.1 \times \ln(2) \) にして、10mあたり半分に減る減衰定数 (0.60dB/m) に、また線路長も \(l=10\mathrm{m}\) としました。

それらの条件で描画したグラフが 下の fig12.2 です。

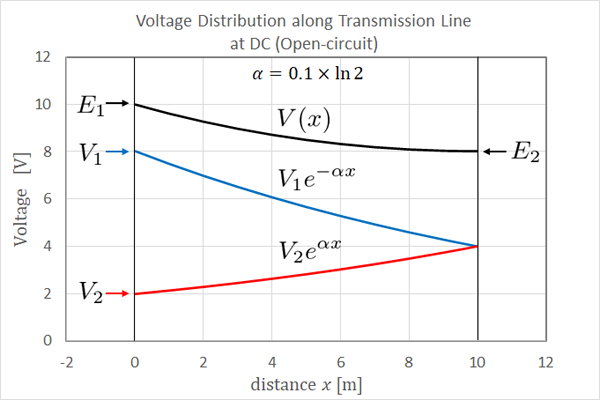
Voltage Distribution along Transmission Line at DC (Open-circut)

fig12.2 開放線路の電圧分布

始端に加えた 10V は、終端へ到達するまでに 8V へ減衰していることが分かります。が、少し変ですね。 減衰定数の設定上は 5V になりそうですが全然足りません。一応再計算しみましょうか。

\begin{eqnarray} e^{- \alpha l } &=& \exp (- 0.1 \times \ln 2 \times 10) \\ &=& \exp(- \ln 2 )\\ &=& \frac{1}{2} \end{eqnarray}
やっぱり、違わない…のです。

しかしながら、 \(V_1\) 項は 8V → 4V に減衰してますし、 \(V_2\) 項は 2V → 4V になってますので、各項を個別で見れば確かに1/2の係数になっています。

ここでミステリーとして復活するのが \(V_2\) 項。抵抗のみの回路に電圧を加える時、途中で電圧が上昇することは物理的にあり得ません。 あり得るとしたら、回路の途中に電源がある場合だけです。

すると、この昇圧していく \(V_2\) 項。 終端→始端という方向で影響を及ぼすものと考えるしかないのです。そしてその見えない電源は終端に生じた電圧しか見当たりません。

\(V_1\) 項の電圧が減衰し 4V になりますが、その 4V が電源となってそのまま始端へ向かう流れを生んでいるわけです。つまり鏡面反射と同等の現象がここで生じています。 ちょうど x=10m で折り返したようなグラフになっているのはそのせいです。終端に到達した 4V が 100% 反射。 合計 8V の終端電圧を生じているのですね。そして 反射した 4V が始端に 2V の影響を与えている図式。

ただし、ここで考えているのは直流ですから反射現象は実際に見えません。正確には回路方程式を満たすよう電圧電流のバランスがとれた状態と言うのが正しい表現でしょう。 始端に加えた 10V の印加電圧は 8V しか有効に伝送路内に注入できておらず、反射成分（に相当する）電圧が減衰しながら「戻ってきた」 2V と合わせた 10V が電池電位と平衡しています。

実際に、時間変化を伴う交流やステップ電圧（階段波）を入れられるならば、上記の理屈でリアルに反射が生じるのを観測するこができます。（もちろん真に R と G のみの回路構成では時間遅れがないので無理なんですが。）

開放線路の電流分布状態

では、次に電流分布をみてみます。

\begin{eqnarray} I(x) &=& I_1 e^{-\alpha x} + I_2 e^{\alpha l} \\ &=& \frac{E_1}{Z_c} \left( V_1 e^{-\alpha x} - V_2 e^{\alpha l}\right)\\ &=& \frac{E_1}{Z_c} \left(\frac{e^{-\alpha x}}{1+e^{-2 \alpha l}} - \frac{e^{\alpha x}}{ 1 + e^{2 \alpha l}} \right) \end{eqnarray}
が開放線路－電圧源接続時における電流分布式の詳細ですが、特性インピーダンス \( Z_c \) を 1Ω とし、それ以外のパラメータは電圧分布と全く同じにしてあります。

開放端なので、終端に電流が流れることはできず \(J_2 =0\) が境界条件です。

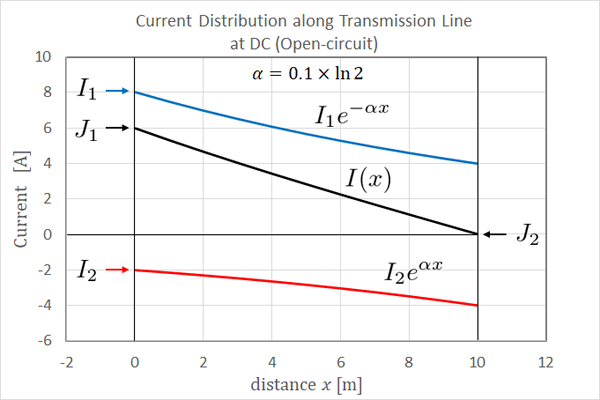
Current Distribution along Transmission Line at DC (Open-circut)

fig12.3 開放線路の電流分布

電圧分布図と類似しつつも、決定的に違うのは \(I_2\) 項が負の値になっていることです。

始端から終端へ向かって減衰する \(V_1 \) に合わせて \(I_1\) も 8A → 4A へ減少するのがよくわかります。 ところが、その電流は -100% 反射相当です。

負電流というのはそもそも「方向が逆になった」という状況に過ぎません。電圧が終端で +100% 反射してきたと考えると、電流の方は負の値にならざるを得ないのです。

その結果、正の電流と反射相当の負の電流がキャンセルしあって終端では電流が流れず \(J_2 =0\) となっているのですね。

反射電流成分が 4A 生じ、 2Aに減衰して始端に戻ってきています。結果として始端では 8A 送って 戻りが 2A 、合計で 8 - 2 = 6A が電池から伝送路に流れ込む電流値になります。

ここまでのまとめ

片端を開放した分布定数回路では、たとえ直流であっても終端で反射を生じていると考えた方が合理的。（厳密にはRG分布で始端と終端の時間差がないので反射現象が生じていたとしても観測はできない。あくまでそのように回路網のバランスが取れているという解釈しかできない。）

少なくとも、終端を開放したときは減衰定数 \( \alpha \) 通りに電圧・電流が減衰してくれていない。ただし、始端→終端、終端→始端の成分ごとに分けた項は定数にしたがって減衰している。

開放端では電圧が +100% 反射しており2倍の電圧として終端に現れている。また、電流は -100% の反射影響で 終端電流 0A の条件を満足している。

次ページへ続く