16.短絡線路の具体的な電圧電流分布

設定条件

前ページで計算した短絡端をもつ線路の解を実際にグラフで見ていきたいと思います。

fig.16.1 は具体値を想定した条件を描いた図です。印加電圧 E1 は 3V と設定し、特性インピーダンスは 1Ω 、そして減衰定数は 10m でちょうど半分になる量を設定してあります。開放端と設定電圧が違う(10V⇔3V)のは両端で整数解になるよう調整しただけです。

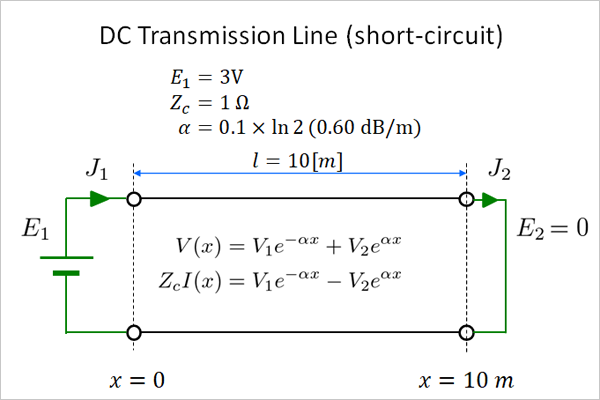
fig16.1 短絡線路（電圧印加）

短絡線路の電圧分布

Voltage Distribution along at DC (short-circut)

fig16.2 短絡線路の電圧分布

\[ V(x)|_{\mathrm{short}} = E_1 \left(\frac{e^{-\alpha x}}{1 - e^{-2 \alpha l}} + \frac{e^{\alpha x}}{1 - e^{2 \alpha l}} \right) \tag{16.1} \\ \]

短絡線路では、 3V の入力電圧が終端に到達するときちょうど 0V になるよう全体が調整されています。

そして電圧積分定数 V1 = 4V が印加電圧よりも大きくなっていおり、その成分を見ると減衰定数どおり 2V へ半減ですね。

しかしながら、終端は短絡されているのでその余計な 2V は消えなければなりません。そこで V2 項が上手くキャンセルして、-100%反射に相当する -2V を生じています。終端で発生した -2Vは減衰して始端に戻り -1V に半減して始端到達です。

この結果、始端では 4V - 1V = 3V となりしっかりと電池電圧と平衡がとれている状態なんです。

開放線路の「電流分布」が類似の性質を示していましたが、短絡線路では「電圧分布」にそれが反映されてくるわけです。線形回路の重ねの理がここでも効いてきます。

なぜ、積分定数が印加電圧より大きくなってしまうのかと、素朴な疑問が湧いてきますが、この点はあとで考察しようと思います。

短絡線路の電流分布

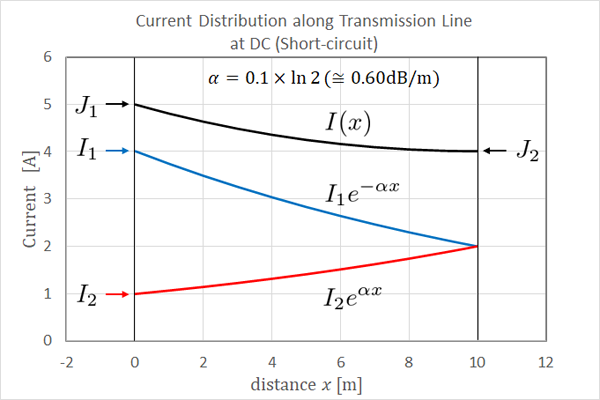
Current Distribution along at DC (short-circut)

fig16.3 短絡線路の電流分布

\[ I(x)|_{\mathrm{short}} = \frac{E_1}{Z_c} \left(\frac{e^{-\alpha x}}{1 - e^{-2 \alpha l}} - \frac{e^{\alpha x}}{1 - e^{2 \alpha l}} \right) \tag{16.2} \\ \]

電流は、印加電圧 3V / 特性インピーダンス 1Ω= 3A よりも大きな電流(5A)が流れ込んでいます。

電流積分定数は I1=4A で終端で 2A に半減。そして終端では電流がそのまま「逆流」してきて始端に 1A の戻り電流が到達。イメージでいえば終端側に電流が引っ張れられる感じでしょうか。結果として 4A + 1A =5A の電流が電池から流れ込みます。

電池から覗いた線路のインピーダンスは 3V/5A = 0.6 Ω で、終端をショートさせた影響で特性インピーダンスよりも小さい値をとります。

トータルでは入力電流 5A、出力電流 4A の2割減といった状況です。

短絡線路の入力インピーダンス（線路長との関係）

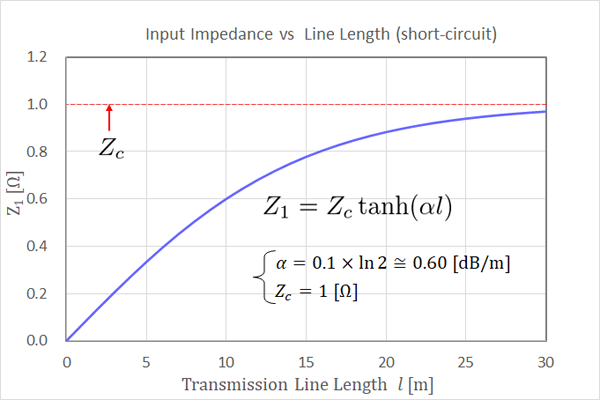
Input Impedance vs Line Length (short-circuit)

fig16.4 線路長と入力インピーダンスの関係

\[ Z_1|_{\mathrm{short}} = Z_c \tanh(\alpha l) \tag{15.10} \]

短絡線路なので、線路長が短いほど抵抗が小さくなりショートした影響が色濃くなります。極限の 0 mm で 0Ω になるものの、この条件下では 1cm あれば 0.7mΩ ぐらい、1m で 70mΩ ぐらい , 10m で0.6Ω ピッタリとなります。

開放線路は距離に反比例して∞からZcの特性インピーダンスへ収束していきましたが、短絡線路はその逆数なので、0ΩからZcへ収束します。いずれにせよ線路損失が大きければ無限長線路特性に近づき、Zc へ落ち着いてしまうのでした。

次ページへ続く