17.電圧・電流積分定数の意味

前ページ

積分定数の解釈

前ページで短絡線路の具体的な分布を見てきました。 その４つの積分定数 \(V_1,V_2,I_1,I_2\) は線路の条件… 終端の状態によって変化するもので 全体の「つじつま」を合わせるように現れる計算上の数に見えます。

\begin{eqnarray} V(x) &=& V_1 e^{-\alpha x} + V_2 e^{\alpha x} \tag{9.3} \\ I(x) &=& I_1 e^{-\alpha x} + I_2 e^{\alpha x} \tag{9.4} \end{eqnarray}

あくまで実際の物理状態は \(V(x),I(x)\) ですし、 \(V_1\) を単独で見ようとも観測しようがなく、物理的実体は無いと解釈することもできます。

一方で、これは何らかの物理状態を表していると考えることも可能そうです。 このページではそのような立場から積分定数を見つめなおすことにします。

開放線路の電圧電流積分定数

終端開放線路（電圧源 \(E_1\) 印加）では 以下の電圧積分定数でした

\begin{eqnarray} V_1 &=& \frac{E_1}{1+e^{-2 \alpha l}} \tag{11.7} \\ V_2 &=& \frac{E_1}{ 1 + e^{2 \alpha l}} \tag{11.8} \end{eqnarray}

電流の積分定数 \(I_1,I_2\) は、特性インピーダンス \(Z_c\) がありさえすれば \[ I_1 = V_1 / Z_c　\ , \ I_2 = -V_2 / Z_c \] と直ちに求まるので、これ以後は片方を省略していきます。

先の具体例では E1=10V を印加したとき V1=8V , V2= 2V 。 終端で電圧が 100% 跳ね返ってきた図(fig.12.2)になります。

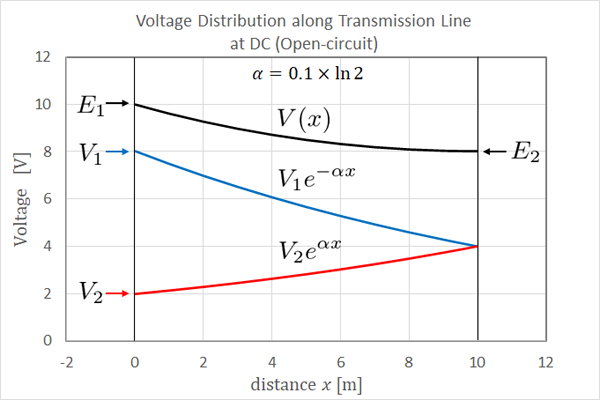
Voltage Distribution along Transmission Line at DC (Open-circut)

fig12.2 開放線路の電圧分布

理論上は R と G しか無い線路なので始端(x=0)から終端(x=l)までの到達時間は 0 なのですが、もし伝搬するのに時間を要していると仮定するならば、これは無限回の反射が繰り返された結果だと解釈できます。

\(V_1,I_1\) は右方向へ「減衰」しながら伝わる成分でした。 \(\exp(-\alpha x)\) 項の定数ですから原点から正の方向の距離で減衰し続ける電圧電流です。

それとは逆に 、 \(V_2,I_2\) は右方向に「増大」しながら伝わるように見える成分でした。見方を変えれば 左方向に「減衰」するという意味であって、\(\exp(+\alpha x)\) 項は右端に原点 x=0 の基準をずらした線路を考えてみると合点がいきます。

そして、開放端(OPEN)では +100% 反射の電圧が生じ、 短絡端(SHORT) では -100% の反射電圧が生じると考えた方が合理的であることを前提とすると、以下のような推移が考えられます。

このように何度も減衰反射を繰り返すときの電圧はどのように加算されるのか？　まずは 「右方向V1」 成分だけを考えていきます。

始端に電池をつなぐと \(E_1\) が始端に生じて右方向へ進んでいくはず。なので、 \[ V_1 = E_1 \tag{17.1} \] これは無限長線路の結果と同じです。

それが終端に到達したときは \(E_1 e^{-\alpha l}\) に減衰しており、 そこで +100% 反射して戻ってくる頃には往復で２倍の減衰を受けるので \( E_1 e^{-2\alpha l}\) の電圧が始端に到達する計算です。

始端では -100 % 反射して「右方向V1」の成分となりますが、その時の電圧は \[ V_1 = E_1 - E_1 e^{-2\alpha l} \tag{17.2} \] と負数が加算となります。つまりV1は減るんですね。第1回目の再反射では負ですが、第2回目以後の再反射は + - + - と交代することに注意してください。

これらの合計を式で表せば
\[ V_1 = E_1 - E_1 e^{-2\alpha l} + E_1 e^{-4\alpha l} - E_1 e^{-6\alpha l} + \cdots \tag{17.3} \]

この無限級数をまとめて \[ V_1 = E_1 \sum_{n=0}^{\infty} (-1)^n e^{-2 n \alpha l} \tag{17.4} \] とすると、数式的にはキレイで必要十分なものの、ここから見慣れた形に変換するのは少々面倒なので、 \(x= \exp(-2\alpha l)\) として少し代数計算をしてみます。

\begin{eqnarray} V_1/E &=& 1 - x + x^2 + x^3 - x^4 \cdots \\ &=& (1 + x^2 + x^4 + \cdots ) \\ & & \ \ -( x + x^3 + x^5 \cdots) \\ &=& (1 + x^2 + x^4 + \cdots ) \\ & & \ \ -x ( 1 + x^2 + x^4 \cdots) \\ &=& \frac{1}{1-x^2} - \frac{x}{1-x^2} \\ &=& \frac{1-x}{1-x^2} \\ &=& \frac{1}{1+x} \end{eqnarray}
すなわち、 式(17.3)は
\[ V_1 = E_1 \sum_{n=0}^{\infty} (-1)^n e^{-2 n \alpha l} = \frac{1}{1+e^{-2\alpha l}} \tag{17.5} \]
であり、式(11.7)と完全一致することが確認できました。

直流伝送路なので解釈の問題はありますが、電圧積分定数 \(V_1\) は線路内に存在する無限回反射した電圧のうち、「始端」を指定して「右方向成分」の総和をとったものと等しいのでした。

同様に \(V_2\) は「始端」における無限回反射の「左方向成分」の総和に等しくなります。要するに終端から戻ってきて、まだ再反射する直前の総和ですね。一応確かめてみましょう、 始端では \(V_2 = E_1 - V_1 \) になることも利用できますが、一応無限級数から。

\[ V_2 = E_1 e^{-2\alpha l} - E_1 e^{-4\alpha l} + E_1 e^{-6\alpha l} + \cdots \tag{17.6} \]
再び \(x= \exp(-2\alpha l)\) と単純化して計算すると
\begin{eqnarray} V_2/E &=& x - x^2 + x^3 - x^4 + \cdots \\ &=& x (1 - x + x^2 - x^3 + \cdots )\\ &=& x \left( \frac{1}{1+x} \right) \\ &=& \frac{e^{-2\alpha l}}{ 1+ e^{-2\alpha l}} \\ &=& \frac{1}{1+ e^{2\alpha l}} \end{eqnarray}
まとめて、
\[ V_2 =E_1 \sum_{n=1}^{\infty} (-1)^{n+1} e^{-2 n \alpha l} = \frac{E_1}{1+ e^{2\alpha l}} \tag{17.7} \]

結局、これも無限反射の重ね合わせと一致していることがわかります。なお、この V2 の総和は n=1 から始まっていることに注意してください。

積分定数の解釈まとめ

どうやら積分定数は単なる境界条件の調整項というわけでなく、線路内で減衰しながら無限回反射した成分の総和であると考える方が理に適っているようです。実際に計算してみるとわかりますが短絡線路のときも、また電源が電流源（OPEN端相当）であってもこの考え方は成立します。

反射成分が生じない無限長線路や特性インピーダンスでの終端では、片方の積分定数が消えてしまい、 V1 が印加電圧 E1 に等しく,また I1 が印加電流 J1 に等しくなることとも整合性が取れます。

また、方程式に現れる積分定数から線路内の「電圧」「電流」は一定の割合でしか減衰することができないことが見て取れます。 入力->出力が必ずしもケーブルの減衰定数と一致しないのは、両端で電圧・電流が反射した影響なのでした。

次ページへ続く（作成中）

付録 無限級数の和の公式

このへんで、ちょっと使うかもしれない冪級数公式。 \(|x| \lt 1\) でないと発散するので注意。
\begin{eqnarray} 1 + x + x^2 + x^3 + \cdots &=& \frac{1}{1-x} = \sum_{n=0}^{\infty} x^n \\ x + x^2 + x^3 + \cdots &=& \frac{x}{1-x} = \sum_{n=1}^{\infty} x^n \\ 1- x + x^2 -x^3 + \cdots &=& \frac{1}{1+x} = \sum_{n=0}^{\infty} (-1)^n x^n \\ x - x^2 + x^3 - \cdots &=& \frac{x}{1+x} = \sum_{n=1}^{\infty} (-1)^{n-1} x^n \end{eqnarray}