ゲルマラジオの感度はどれぐらいなのか?
はじめに
ゲルマラジオは数あるラジオの中で「最も感度が低い」ことは当たり前の事実です。そのせいなのか、ゲルマラジオ工作をしている折にはこんな思いに駆られることがありました。
「どこまで感度が上がるのだろうか?」
同じような疑問を持たれた方も多いかもしれません。
そんな思いを最初に抱いたのは今を遡る事、約20年前。小学生の頃でした。その頃は電話級アマチュア免許を取り立ての頃で、さすがに歯が立ちませんでした。時がたち、本格的にゲルマラジオに取り組み始めてから早1年が経って、ようやく「感度」を計算する目途が立ってきました。
このページでは、ゲルマラジオの感度を求めるべく、感度とは何かというところから始め、標準のゲルマラジオを想定した上で、その感度を理論的に追求していきます。ゲルマラジオを作りたい初心者向けのコンテンツではありませんが、なるべく平易な表現になるよう努力したつもりです。
分かりにくい部分や、疑問、誤りなどがございましたらメールにてご指摘いただけると幸いです。
1.2 おことわり
本ページで解析した方法は、あくまで簡易な理論的計算にもとづいているので、実際の感度については、より実験的な検証を加える必要があります。そのまま信用せずに参考としてご覧ください。
本ページの目的の一つは、「どうすれば感度が求められるか」であったりします。個々の計算結果よりは、むしろこちらの方に重点を置いたつくりになっています。
1.3 目次
2 ゲルマラジオにおける感度の定義
2.1 出力信号電力による定義
一般的なアナログ受信機の感度測定に用いられるパラメータは、S/N比が重要となります。しかしながら、ゲルマラジオは無増幅のため増幅に起因するノイズは存在しないので、復調歪みだけを考慮すればよいでしょう。そのため感度を定義するためには、復調信号の大きさ(パワー)だけでよいと考えられます。
次に、どのぐらいの出力を感度の定義に採用するかにあたっては、使用するイヤホンやヘッドホン(以下レシーバと言う)と個人の聴感の差異が大きく影響することになります。
そこで、一般に市販されるレシーバを試験したところ、周波数1kHz、インピーダンス10kΩの条件下において、3~6mVrmsが十分に認識できる最小電圧値でした。
実験に使用したのは、セラミック圧電素子タイプのクリスタルイヤホン(Z=8kΩ@1kHz)と音楽用高感度ヘッドフォン(オーディオ・テクニカ社製ATH-SJ3/Z=32Ω:114dB SPL/mW)にトランス(春日無線変圧器製OUT-41-357/7kΩ:8Ω)を組み合わせたものの2種類です。
これ以下のレベルでは一般市販品を使用してラジオ放送を受信する目的のためには実用的ではないと判断し、レシーバの最小感度を5nW(-53dBm)と設定することにしました。
上記のレシーバに置き換えれば、10kΩ負荷で10mV(実効値で7.07[mVrms])の信号出力が得られる電界強度Eを受信感度と定義することになります。電力で定義するのは、使用レシーバに様々なインピーダンスが考えられるからであり、電圧で感度を定義しにくいからです。
より高感度のレシーバを使用し、さらに小さい音量でも感度が定義可能ではありますが、現状では5nWを実用レベルと仮定するものとします。
2.2 変調度と周波数
AM受信機は同じ平均電界強度であっても変調度が異なると出力が変化します。そのため、標準の30%[12] にて計算することに決めました。また、キャリア周波数は1MHzとします。
2.3 その他の問題
クリスタルイヤホンなどの容量性負荷を駆動する場合は、実効電力での定義は不適当であるかもしれません。皮相電力で5nWとするべきかどうか別途検討する必要があります。
3 標準ゲルマラジオの構成
ゲルマラジオの一つの特徴は、無数の構成が考えられることです。アンテナからレシーバに至るまで多種多様な組み合わせがあり、加えて、一つの構成要素の性能が全体に大きな影響を与える可能性が高いのです。
増幅素子を有するラジオ受信機では、不確定要素を抑える設計が容易ですが、ゲルマラジオは一要素が全体と密接に影響しあっているため、性能に影響する要素を一つづつ検討する必要があると思われます。
不確定要素をなるべく抑制するために、広く一般に用いられる方法の中から計算が容易となる組み合わせを選び、標準構成を決定することとしました。
3.1 アンテナ
アンテナは実際の使用状況と計算の容易さから、ループアンテナを想定します。個人が中波帯の実用アンテナとして数十mを超える「垂直アンテナ」を使用するのは困難ですし、水平部が長いアンテナは垂直偏波が伝搬の主である中波帯の環境下では簡易計算が困難です。
ループアンテナであれば測定器に用いられるほど感度が正確に計算でき[6]、アースが不要であることも不確定要素を減らすのに有効と考えました。
ループは室内でも使用可能な範囲で、製作の簡便さを考慮し、正方形で1辺の長さが50cm、直径0.6mmの銅の単線を仮定します。
3.2 同調回路
同調回路はループアンテナのインダクタンスを利用してアンテナと兼用する一般的な方法を採用しました。当面は計算を簡略化するためタップまたはピックアップコイルは考慮せず、アンテナ回路と検波回路を直結する構成とします。
3.3 検波回路
検波回路はごく標準的な包絡線検波回路とし、ダイオードの逆方向飽和電流を1μA、負荷抵抗を10kΩと設定しました。特に逆方向飽和電流は使用するダイオードの特性や周囲温度によって数桁異なるほど変動しやすく最大の不確定要素となりえます。
ここでは測定に使用したサンプル(1SS108の実測値3.2μA、1N60の実測値0.8μA)を考慮し、ばらつきが1桁のオーダであると見て1μAと設定することに決めました。無論その他の値もシミュレーションを実施し影響を考慮する必要があります。
なお、負荷抵抗Rは受話器そのものであるとみなして10kΩとしています。この値は通常100kΩ以上が用いられることが多く(おそらく、ロッシェル塩タイプのクリスタルイヤホンを想定した値)、それと比較して、かなり低い値ではあるのですが、レシーバのインピーダンス実測結果を考慮すると、この値のオーダが適当であると考えられます。
必要に応じて低周波トランスを用いてインピーダンス変換も可能ですが、それは別の機会に検討しましょう。fig.1に出来上がった標準ゲルマラジオの構成を示します。
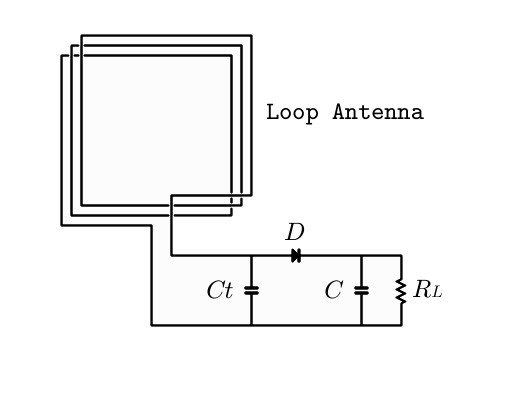
fig1.標準ゲルマラジオの構成図
4 ループアンテナの計算
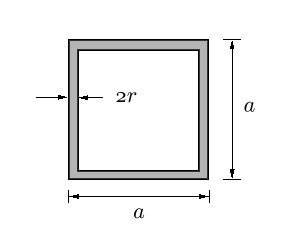
fig2. 正方形ループアンテナ
4.1 ループインダクタンス
fig2に示した1回巻き正方形ループアンテナのインダクタンスL1は
\[
L_1 = 0.8a \left( \ln \frac{2a}{r}-1.467 \right) \ [\mu H] \tag{4.1}
\]
で計算できます[3]。
ここでa[m]は1辺の長さ、r[m]は導線の半径です。a=0.5[m]、r=0.3[mm]としたときのインダクタンスL1は2.66[uH]になります。
このアンテナをそのまま同調回路の一部として使用するためには、市販バリコンの容量制限から300uH前後のインダクタンスが必要となるので、2.66uHのままでは大幅に不足してしまいます。そのためインダクタンスを増加させるには巻き数Nを増やして使用することになるのですが、N回巻きのインダクタンスLNは、
\[
L_N \simeq N^2 L_1 \tag{4.2}
\]
であり、巻き数の2乗に比例して増加します。(厳密には幅を考慮しない式のため、実際には式(4.1)よりインダクタンスが低下します。)
LN=330uHとするときのNを求めると、
\[
N = \sqrt{\frac{L_N}{L_1}} = \sqrt{\frac{330}{2.66}} = 11.14 \tag{4.3}
\]
であるので、巻き数は11回が適当となります。このときのインダクタンスは、L11=322uHとなり、同調回路に適した値となりました。
(※本節の計算は簡易的なものであり、より詳細なインダクタンスの計算[4]については、別途紹介する予定です。)
4.2 ループアンテナの直流抵抗
ループアンテナの直流抵抗RDCは、
\[
R_{DC} = \rho \frac{l_w}{\pi r^2} \tag{4.4}
\]
で計算できます。ここで、ρは導線の体積抵抗率、lwは導線の全長、rは(円形断面の)導線半径です。銅線の全長lwは
\[
l_w = 4aN = 4 \times 0.5 \times 11 = 22 \ \mathrm{[m]} \tag{4.5}
\]
ですので、銅の体積抵抗率ρ=1.8×10-8 [Ω・m]、銅線半径r=0.3[mm]を式(3.4)に代入すると、
\[
R_{DC} = \frac{1.8 \times 10^{-8} \times 22}{3.141 \times (3 \times 10^{-4})^2} = 1.40 \ \mathrm{[\Omega]}
\]
が得られました。
この直流抵抗RDCは考え得る最小の抵抗値であって、高周波領域ではそのまま適用ができません。交流に対する効果の影響により非常に抵抗値が大きくなります。
適用条件を吟味する必要があります。
4.3 ループアンテナの高周波抵抗
導線に高周波電流が流れる際、表面に電流が集中する現象が生じるため、高周波抵抗は直流に比べて大きくなる「表皮効果」が現れます。電流が内部に流れることができないために実効的な電線面積が減少してしまうのが原因です。(本質的に表皮効果を避けることは不可能ですが、リッツ線などの特殊電線を使用することで高周波抵抗を減少させることは可能)。
電線に高周波電流が流れた時、電流密度が電線表面の電流密度に比べて1/e=37%に減少する皮の厚さ(表皮深さ)をδとすると、
、μを銅線の透磁率、σを導電率として、
\[
\delta = \sqrt{\frac{2}{\omega \mu \sigma}} \tag{4.6}
\]
となります。
もし、導体の材質を電気銅(1/58[S/m] =1.72[Ω・m])とすれば、
\[
\delta \ \mathrm{[mm]} \simeq 0.0661 \sqrt{\frac{1}{f \mathrm{[MHz]}}} \tag{4.7}
\]
となり、周波数が1[MHz]であれば、δ=66[um]と計算できます。使用銅線の半径が0.3mm=300[um]ですから、実効面積が半減していることがわかります。
実際の高周波電流の分布は中心に向かって指数関数的分布になっているのですが、表面からδだけの範囲に一定の電流密度で流れているのと同等に扱うことができるので、
高周波抵抗RHFを求めるには表皮の面積Sを求めるだけでよいです。
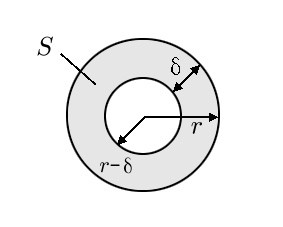
fig3. 導線の断面図(表皮効果)
よって、電流が均等に流れていると仮定した領域の面積Sを求めてみると、
\begin{eqnarray}
S & = & \pi(r^2-(r-\delta)^2) \\
& = & \pi(2 \delta r - \delta^2) \\
& \simeq & 2 \pi \delta r, \ \ (\delta \ll r) \tag{4.7}
\end{eqnarray}
となります。
δ=0.07[mm],r=0.3[mm}を代入すれば、面積S=1.32 ×10-7 [m2]となり、高周波抵抗RHFは=3.0[Ω] となりました
(もう少し精度良く計算して3.4Ω程度)。ただし、実際の抵抗は表面抵抗の状態、近接効果などにより増加するため、余裕をみて、RHF=5[Ω]に設定することにします。(これでも結構低めの想定です。)
4.4 ループアンテナの実効長と等価回路
アンテナを電界強度Eの場に設置したとき、無負荷のアンテナに誘起する電圧をVoとすると、その比
\[
h_e = \frac{V_o}{E} \tag{4.8}
\]
を実効長または実効高と呼びます。仮想的なアンテナの長さで単位は[m]で表します。
最初に想定した微小ループアンテナの実効長heは、Nを巻き数、Aをループ面積、λを波長とすれば
\[
h_e = \frac{2 \pi N A}{\lambda} \tag{4.9}
\]
と理論的にもシンプルとなります[5]
4.1節の結果から、N=11[回]、A=0.52=0.25[m2]、λ=300/f[MHz]=300[m]を代入すれば、実効長heは、
\begin{eqnarray}
h_e &=& \frac{6.282 \times 11 \times 0.5^2}{300} \\
&=& 57.6 \times 10^{-3} \mathrm{[m]} \tag{4.10}
\end{eqnarray}
となり、5.76cmとなりました。
この程度の実効長は、同一条件での1/4波長垂直接地アンテナ(高さ75m)の実効高48[m]と比較すると、約800分の1という極めて小さい値になることが分かります。
要は標準アンテナと比較して感度が悪いと言う意味なのですが、AMラジオ帯域ではサイズ的にこれでも大きいアンテナの部類でもあり、いかに放送波が強力であるか
を実感することができます。
なお、厳密にいえば実効長が小さくとも受信感度が劣ることを意味しません。ですが一般には、そのようなアンテナから電力を取り出すのは難しいため、低効率になりがちです。
以上の結果を等価回路として表すとfig.4となります。
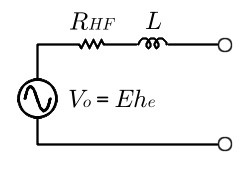
fig4. アンテナ等価回路
※注:fig.4におけるアンテナの放射抵抗成分は、1[mΩ]以下となるため無視しています)
5 アンテナ回路と同調回路
5.1 同調容量
アンテナのインダクタンスLが求められているので、その同調容量Ctは
\[
C_t = \frac{1}{\omega ^2 L} = \frac{1}{4 \pi^2 f^2 L} \ \mathrm{[F]} \tag{5.1}
\]
となるので、L=322[uH]、f=1[MHz]を代入して、Ct=79[pF]となります。
5.2 同調時の無負荷Qと等価回路
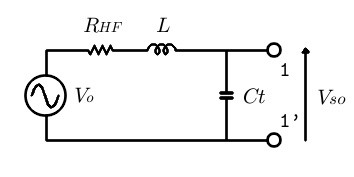
fig5. アンテナ及び同調回路の等価回路
図5はアンテナにキャパシタCtを接続して共振回路としたときの等価回路です。図5において、LとCtは電圧源側から見て直列共振しているため、
インピーダンスは0です。すなわち回路インピーダンスはRHFのみとなるため、その回路電流Iは
\[
I = \frac{V_o}{R_{HF}} \tag{5.2}
\]
と計算されます。
その電流によって、端子1-1'に誘起される電圧をVsoとすると、Ctの持つインピーダンスと電流Iとの積になるので、
\[
V_{so} = \frac{I}{j \omega C_t} = -j \frac{V_o}{\omega C_t R_{HF}} \tag{5.3}
\]
Vsoは通常、共振回路の性質によりVoよりも高い電圧となるので、その電圧上昇比をQoとすると式(5.3)より
\[
Q_o = \frac{1}{j \omega C_t} \tag{5.4}
\]
とまとめられて、Vsoは
\[
V_{so} = -j Q_o V_o \tag{5.5}
\]
とも表すことができます。
このQoは共振回路の無負荷Qと呼ばれる量です。(Qには単位がありません)式の中の"-j"はVoとの位相差が90度であることを表すだけなので、ゲルマラジオ用としては無くても支障が無いパラメータです。そのため、以降は絶対値だけを扱うことにします。
式(5.4)に、Ct=79[pF] 、f=1[MHz] 、RHF=5[Ω]を代入すると、Qo=405となって、端子1-1'にはアンテナ誘起電圧Voの405倍もの共振電圧が生じることを示しています。
現実にはキャパシタの損失分や経験値などから、もう少し小さくなる(100~200)はずですが、ここでは損失がRHFのみとして仮計算しておきます。
5.3 回路の直並列変換
(5.4)節では、共振回路に何も接続しない無負荷の状態を計算していますが、実際には検波回路が負荷となるため、これを影響に入れなくてはなりません。そのため、負荷を接続したときに計算がしやすいよう、直並列変換を行います。

fig.6 等価回路の直並列変換
fig.6 の左側が、前節での等価回路に相当します。端子1-1'から見たインピーダンスは、電圧源を短絡すればいいわけです。ここで、直列抵抗RHFの影響を、fig.6 左側の並列抵抗Rpに等価変換するためには、
\[
R_p = \frac{\omega ^2 L^2 }{R_{HF}} \tag{5.6}
\]
とします。(ただし、直列抵抗RHFがLのインダクタンスに比べて十分小さいという仮定の元に変換が行われているため、RHFが極端に大きい回路では成立しないことに注意する必要があります。)
回路は共振状態ですので、$X_L = \omega L = 1/\omega C $が成立しているために、以下のようにも変換が可能です。
\begin{eqnarray}
R_p &=& \frac{\omega ^2 L^2 }{R_{HF}} \\
&=& \frac{1}{\omega ^2 C_t^2 R_{HF}} \\
&=& \frac{1}{R_{HF}} \cdot \frac{L}{C_t} \\
&=& X_L Q_o \tag{5.7}
\end{eqnarray}
式(5.7)に、ω=6.28×106[rad/s]、Ct=79[pF]、RHF=5[Ω]を入れると、Rp=819[kΩ]なる並列抵抗値が得られます。これは共振回路のインピーダンスに相当する量です。
単純には、共振時のLまたはCのリアクタンスがQ倍されたと考えると分かりやすく、Qが高いほどRpも高くなる寸法です。
5.4 電流源の計算
図6の等価回路には電源が無いままですので、これに電流源を付加したのが図7です。

fig.7 電流源のあるアンテナ-同調回路の等価回路
電流源Iの値を求めるには、1-1'間の電圧がVsoであることと、式(5.3)(5.7)を利用します。回路は共振状態にあるので、電流は全てRpに流れるとみなしてもよく
\begin{eqnarray}
I &=& \frac{V_{so}}{R_p} \\
&=& \frac{V_o}{\omega C_t R_{HF}} \cdot \omega ^2 C_t^2 R_{HF} \\
&=& \omega C_t V_o \tag{5.8}
\end{eqnarray}
と、簡単な結果になりました。
5.5 負荷接続時のアンテナ-同調回路
アンテナ-同調回路の最後の計算目的は、負荷Ziを接続したときの1-1'間の電圧Vslを求めることにあります。(記号をZiとしたのは、検波回路の"入力インピーダンス"が負荷となるからです。またVslはV source loadの意。)
負荷を接続したときの等価回路を図8に示します。
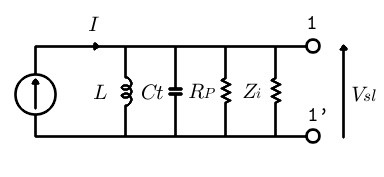
fig.8 負荷接続時のアンテナ-同調回路の等価回路
等価共振回路インピーダンスRp、負荷Ziに流れる電流をそれぞれIR、IZとおくと、
\[
I = \frac{V_{sl}}{I_R} + \frac{V_{sl}}{I_Z} \tag{5.9}
\]
。式(5.8)より$ I=\omega C_t V_o $であるので、式(5.9)に代入して
\[
V_{sl} \left( \frac{1}{R_p} + \frac{1}{Z_i} \right) = \omega C_t V_o \tag{5.10}
\]
。式(5.10)をVslについて解くと
\begin{eqnarray}
V_{sl} & = & \cfrac{\omega C_t V_o}{\omega ^2 C_t^2 R_{HF} +\cfrac{1}{Z_i}} \\
& = & \cfrac{V_o}{\omega C_t R_{HF} + \cfrac{1}{Z_i}} \\
& = & \cfrac{V_o}{\cfrac{1}{Q_o}+\cfrac{1}{\omega C_t Z_i}} \tag{5.11}
\end{eqnarray}
ここで、式(5.11)の中にある、$ \omega C_t Z_i $なる量は、無損失の共振回路の負荷としてZiのみが接続されているときのQに相当する量です。
すなわち
\[
Q_z = \omega C_t Z_i \tag{5.12}
\]
として、Qoの仲間として扱うとき、この量を「外部Q」と呼びます[8]。
式(5.11)を式(5.12)を利用して書き直せば、
\[
V_{sl} = \cfrac{V_o}{\cfrac{1}{Q_o}+\cfrac{1}{Q_z}} = Q_L V_o \tag{5.13}
\]
と、非常に見通しよくまとめられます。
ここで、QLは負荷Qとか実効Qと呼ばれる量です。式(5.13)をみると、負荷Qは並列抵抗を求めるときと同様の形を取っていることが分かります。すなわち、外部Q、無負荷Qをそれぞれ抵抗とみなしたとき、その並列抵抗の値を求めると負荷Qの値と一致するのです。このことはQを考える際に非常に役立ちます。
(補足:Qが並列抵抗と同様に求められるのは、裏で実際に並列抵抗を求める操作をしているからなのです。)
一例として、Zi=50[kΩ]の負荷を接続したときのQを求めてます。この負荷は一般に十分大きな抵抗であるとみなせるのですが、キンキンに共振している共振回路にとっては重い負荷となり、外部QはわずかにQz=25です。結果、負荷QはQL=23にまで低下してしまいます。前提としている無負荷Qが$Q_o=405$という大きな値でありながら、事実上、外部Qが負荷Qを決定してしまうのです。
よって、ゲルマラジオの同調回路の設計においては、負荷Qを意識しながら進めなくてはならないことがわかります。
5.6 アンテナ-同調回路のまとめ
負荷Ziの検波回路を接続したときの、アンテナ-同調回路の出力電圧Vslは
\begin{eqnarray}
V_{sl} & = & Q_L V_o \tag{5.13} \\
V_o & = & E h_e = 2 \pi NAE/\lambda \tag{4.9} \\
Q_L & = & \cfrac{1}{\cfrac{1}{Q_o}+\cfrac{1}{Q_z}} \tag{5.13} \\
Q_o & = & \frac{1}{\omega C_t R_{HF}} \tag{5.4} \\
Q_z & = & \omega C_t Z_i \tag{5.12}
\end{eqnarray}
ここで、
- $V_{sl}$
- 負荷(検波器)接続時の同調回路共振電圧[V]
- $V_o$
- 無負荷時のアンテナ誘起電圧[V]
- $Q_L$
- 同調回路の負荷Q
- $Q_o$
- 同調回路の無負荷Q
- $Q_z$
- 同調回路の外部Q
- $\omega$
- 角周波数$=2 \pi f \ \mathrm{[rad/s]}$
- $C_t$
- 同調回路の静電容量[F]
- $Z_i$
- 負荷(検波器)の入力インピーダンス[Ω]
- $N$
- ループアンテナの巻き数
- $A$
- ループアンテナの面積[m2]
- $E$
- 受信点の電界強度[V/m]
- $\lambda$
- 受信波長[m]
- $h_e$
- アンテナの実効長[m]
本節までの計算で、電界強度と負荷インピーダンス、及び同調回路共振電圧の関係が求められました。
6 検波回路
6.1 検波回路の入出力特性
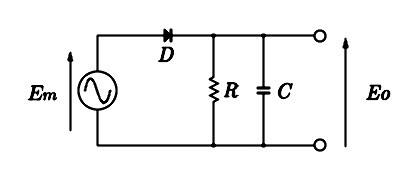
fig.9 包絡線検波回路
fig.9に示す包絡線検波回路の出力電圧Eoは、別ページで導出したとおり、
\begin{eqnarray}
E_o &=& V_T \ln \left[ \mathrm{I_0} \left(\frac{E_m}{V_T} \right) \right] \\
&& \ \ \ - V_T \left( 1 + \frac{E_o}{R I_s}\right) \tag{6.1}
\end{eqnarray}
です。ここで各変数は、
- $E_o$
- 出力電圧 [V]
- $E_m$
- 入力交流振幅[V]
- $V_T$
- ダイオードの熱電圧 $=kT/q \simeq 26\mathrm{[mV]}$@室温。
- $R$
- 負荷抵抗[Ω]
- $I_s$
- ダイオードの逆方向飽和電流 [A]
- $\mathrm{I_0}(x)$
- 第1種0次変形ベッセル関数
- $\mathrm{I_1}(x)$
- 第1種1次変形ベッセル関数
- $\ln(x)$
- 自然対数
式(6.1)は特殊な条件を与えない限り解析的には解くことができず、近似式(Loyka式[9])を用いても、ゲルマラジオの感度を求めるには最も精度の悪い(最大で40%弱)範囲にあたるため、手計算はちょっと難しそうです。このような場合は、Newton-Raphson法を用いてシミュレーションを行うしかなさそうです。
26mV以下の小信号領域や、1V以上での大信号領域では近似式が使用できるのですが、ゲルマラジオで使用する領域では高精度の近似式が見当たらないのが現状です。以下の議論は、入出力特性グラフが計算できることを前提に進めることにします。
6.2 所要出力を得るのに必要な入力電圧
結論から先に書くと、出力信号電圧の振幅が10mVとなるためには、80[mV]の入力振幅が必要でした。これはシミュレーションを行った結果なのですが、以下に基本的な考えかたを記載します。
まず、検波効率をηとしたときに、その定義より
\[
E_o = \eta E_m \tag{6.2}
\]
が成り立ちます。
ここで、Emは入力RF信号の振幅を表していますが、AM変調波はEmを変化させる変調方式であるので、時間的に変動するパラメータになります。
これを式で示すと、
\[
E_m = E_c (1+ m \cos (pt)) \tag{6.3}
\]
です[10]。ここで、Ecは搬送波振幅、mは変調度(0.3を仮定)、pは変調波の角周波数を表します。
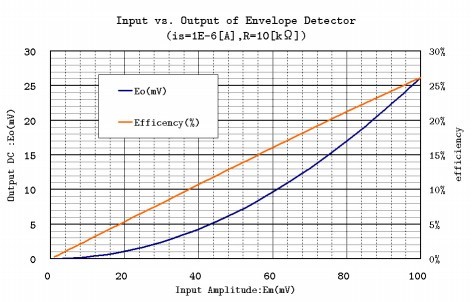
次に、Isを1[uA]、R=10[kΩ]にしたときの検波特性グラフを図10-1に示します。
fig.10-1を見ると、100mV以下のEm入力範囲では、検波効率ηが直線であることから、ほぼ2乗特性であることが分かります。この範囲では入力が2倍になると、出力が4倍となる性質があります。
次の図10-2はEm=300mVまでの範囲について、入出力微分特性を描いたものです。これを見ると約150mV以下であれば、ほぼEmに比例した直線であり2乗特性としてみなせそうです。
(補足:微分値の傾きがEmに1次比例するということは、2乗特性であることを意味します。もし、微分値の傾きが水平ならば線形(直線検波)特性であることが分かります。)
300mV以上のRF入力だとほぼ直線検波領域となっていますが、今求めるべきものは小信号領域での感度ですので、全体を2乗特性として扱うことにします。すなわち、
kを比例定数として
\[
E_o = k E_m^2 \tag{6.4}
\]
と仮定するわけです。
式(6.2)と式(6.4)の関係から
\[
\eta = k E_c \tag{6.5}
\]
また、式(6.4)に式(6.3)を代入すると復調信号Eom(om:output, modulated)が計算できて、
\begin{eqnarray}
E_{om} & = & k E_m^2 \\
&=& k E_c^2 (1 + m \cos(pt))^2 \\
&=& k E_c^2 (1 + 2m \cos pt + m^2 \cos^2 pt) \\
&=& k E_c^2 \left(1 + 2m \cos pt + m^2 \frac{1+\cos 2pt}{2} \right)
\end{eqnarray}
整理して、
\begin{eqnarray}
E_{om} &=& \left(1 + \frac{m^2}{2} \right) k E_c^2 \\
&& \ \ + 2 k m E_c^2 \cos pt \\
&& \ \ \ \ + \frac{1}{2} m^2 k E_c^2 \cos 2pt \tag{6.6}
\end{eqnarray}
一方、無変調時(m=0)のときの出力電圧をEonとすれば(on:output, non-modulated)、
\[
E_{on} = k E_c^2 = \eta E_c \tag{6.7}
\]
になります。
式(6.6)の復調出力を、直流成分VDC、目的信号(復調成分)vs、目的外の成分(歪み)vdstに分類すると
\begin{eqnarray}
V_{DC} & = & k E_c^2 (1+m^2/2) \tag{6.8} \\
v_s & = & 2 k m E_c^2 \cos(pt) \tag{6.9} \\
v_{dst}& = & \frac{1}{2} k m^2 E_c^2 \cos (2pt) \tag{6.10}
\end{eqnarray}
となります。
AM復調された信号は、目的とする信号波成分以外に、歪みを原因とする直流成分(m2/2)がDC成分に加わり、また第2高調波(cos2pt)成分が生じているのです。
特に、この歪み成分vdstは、2乗検波の悪い特徴です。歪み率はm/4で、100%変調時(例えば、音楽放送時のピーク値など)では最高25%にもなります。
さて、ここで目的とする復調波vsに注目すると
\begin{eqnarray}
v_s &=& 2m(k E_c)E_c \cos pt \\
&=& 2 m \eta E_c \cos pt \tag{6.11}
\end{eqnarray}
と変形できて、直線検波時の倍の出力が得られていることも分かります。これも2乗検波の特徴です。
よって、信号波の振幅を
\[
V_s = 2m \eta E_c \tag{6.12}
\]
とおき、これを次のように式変形します。
\[
\eta E_c = \frac{V_s}{2m} \tag{6.13}
\]
式(6.13)は、式(6.7)を使うと、最終的に
\[
E_{on} = \frac{V_s}{2m} \tag{6.14}
\]
と表すことができます。式(6.14)は復調信号の振幅値Vsと無変調時の出力DC電圧値VDCを関係づける重要な式です。
式(6.14)に必要とする復調信号電圧振幅Vsと変調度mを与えてやれば、無変調時の出力DC電圧が計算できて、fig.10-1から入力搬送波振幅Emが求められるのです。
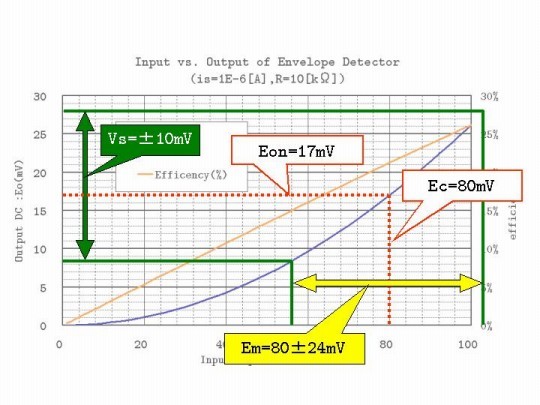
実際に計算をすると、Vs=10[mV]、m=0.3から、Eon=17.1[mV]が得られました。この出力を得るのに必要な入力搬送波振幅は、グラフ図10-1より、Ec=80[mV]と求められます。すなわち、10mVの復調出力振幅を得るには、80mVの入力RF振幅が必要であることが分かりました。fig.11にその手順の一部を示します。
6.3 入力等価抵抗
検波器の入力等価抵抗Refは、入力実効値を2乗して、その回路消費電力で割って定義される値です。(ef:effectiveの意味)。振幅の場合は実効値に換算するために、さらに2で割る必要があります。
\[
R_{ef}=\frac{E_m^2}{2P}
\]
詳細は付録2にて紹介してありますが、ここでは結果だけを書くことにします。
\[
R_{ef} = \frac{1}{2} \cdot \cfrac{E_m}{I_s + \cfrac{E_o}{R}} \cdot \frac{\mathrm{I_0}(E_m/V_T)}{\mathrm{I_1}(E_m/V_T)} \tag{6.15}
\]
ここで、
- $E_o$
- 出力電圧 [V]
- $E_m$
- 入力交流振幅[V]
- $V_T$
- ダイオードの熱電圧 $=kT/q \simeq 26\mathrm{[mV]}$@室温。
- $R$
- 負荷抵抗[Ω]
- $I_s$
- ダイオードの逆方向飽和電流 [A]
- $\mathrm{I_0}(x)$
- 第1種0次変形ベッセル関数
- $\mathrm{I_1}(x)$
- 第1種1次変形ベッセル関数
かなり複雑な関数で、変形ベッセル関数という特殊関数も入っています。解析解が非常に求めにくいので、数値計算シミュレーションするしか方法が見つかりません。ですが、いくつかの信号レベルに分けると、近似値が得られるので、その結果を以下に記します。
まず小信号の極限は、
\[
\lim_{E_m \to 0} R_{ef} = \frac{V_T}{I_s} \tag{6.16}
\]
に収束し、大信号の極限(少なくとも1V以上)は
\[
\lim_{E_m \to \infty} R_{ef} = \frac{R}{2} \tag{6.17}
\]
に漸近します。これは式(3.46)の結果は線形近似理論[10][11]と一致しています。
その中間の領域では、検波効率$\eta = E_o/E_m$を用いて近似的に
\[
R_{ef} = \frac{R}{2\eta} \tag{6.18}
\]
となり、検波効率が高いときには良い一致を示しました。ですが、小信号領域では比較的誤差が大きいため、数値シミュレーションしたグラフより、等価抵抗を求めることにします。
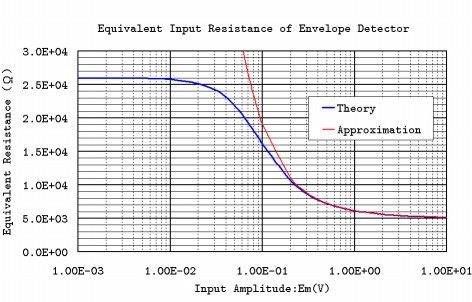
fig.12に式(6.15)のシミュレーション結果を示します。青線がシミュレーション結果、赤線が式(6.18)の近似式です。
グラフより、入力80[mV]のときの入力等価抵抗は18k[Ω]と求められました。(※実際には振幅変調であるために、
時間によって、インピーダンスが変化します。また、負荷となるコンデンサCは、復調信号が交流であるために、多少なりとも影響が出ます。
もう少し詳細な議論が必要になりそうです。実際、参照した論文の中にはこのキャパシタを含んだ負荷の複素インピーダンスが、
各サイドバンドに対して共役インピーダンスとして振舞うと記されています。)
7 感度の最終計算
前節までの計算によって、電界強度と同調回路の出力の関係、並びに所要出力を満たすための検波回路入力レベルとその入力等価抵抗が求められました。
これらの結果を組み合わせていけば、感度が求められるはずです。
7.1 検波器の外部Qと全体の負荷Q
式(5.12)に式(6.15)によって得られた値、Ref=18[kΩ]を代入すると、外部Qは
\begin{eqnarray}
Q_z &=& \omega C_t Z_i \\
&=& 6.282 \times 10^6 \times 79 \times 10^{-12} \times 18 \times 10^3 \\
&=& 8.9
\end{eqnarray}
これと、無負荷時のQo=405を式(5.13)に代入して、
\begin{eqnarray}
Q_L &=& \cfrac{1}{\cfrac{1}{Q_o}+\cfrac{1}{Q_z}} \\
&=& \cfrac{1}{\cfrac{1}{405}+\cfrac{1}{8.9}} \\
&=& 8.7 \tag{7.2}
\end{eqnarray}
すなわち、検波器を接続した状態での共振回路のQは8.7まで低下することになります。
7.2 感度の最終計算
同調回路の出力電圧式(5.13)と、電界強度Eアンテナ誘起電圧の関係式(4.9)をまとめ、Eについて解くと、
\[
E = \frac{V_{sl}}{Q_L h_e} \tag{7.3}
\]
ここに、Vsl=80[mV]、QL=8.7、he=5.76[cm]を代入すると
\[
E = \frac{0.08}{8.74 \times 0.0576} = 0.16 \mathrm{[V/m]} \tag{7.4}
\]
となり、これにてようやく標準ゲルマラジオの感度が160[mV/m]であることが求められました。
7.3 補足
(7.2)節で算出された感度は、数桁外れの誤差を生じていないことぐらいは分かりますが、直感的にはやや低い印象を受けます。
これは、同調回路と検波器を直結することによるミスマッチに起因する問題のようです。もし、タップを用いるなどして、インピーダンスを適切に設定した場合には、E=46mV/m、QL=202が得られました。
なお、タップが理想トランスのように働くと仮定して、タップを2巻き目の位置にとった場合には、
E=47[mV/m]、QL=162となり、もう少しは高感度化が可能である見通しも得られました。
これらは、アンテナの性能によって大きく変わるところでもあり、受信機としてのコア部分、レシーバの部分、アンテナ部分をもう少し分離して整理することが課題です。
一つのパーツが、例えばイヤホンそのものが、アンテナまでに影響するというのが難しさを著しくしていると思います。
別ページにて、一般的なゲルマ受信機部分の実測結果によれば、キャリア基準で-33dBm程度が受信限界となりました。
他方、今回の受信機基準では、キャリア振幅Ec=80mV、検波器の入力Z=18[Ω]から計算して、-37.5dBm程度を想定しています。
受信機はおおむね同程度の感度なので、あと数dB程度の改善ができるとうれしく、アンテナの方は幾らでも工夫の余地ありというところでしょうか。
8 感想など・・・
たかがゲルマラジオとはいえ、理論的な壁-特に検波器-は非常に厚く、ここまで概算を求めるまで約1年を要しました。しかし、実験も検討もまだ緒についたところ。ようやく一里塚に達したようなものです。ゲルマラジオには、まだまだ未知の領域が隠されているように見えてなりません。
それと、上記の議論は時間領域での計算しかしていませんが、古い論文を見ると、包絡線検波器はTVが普及した時期に数多くの伝達関数を求める研究が進められたようで、「周波数変換器としてのダイオード検波器」という手法を目にした時は思わず唸ってしまいました。目からうろこです。
AMスペクトルを見ると、両側波帯を伴ったRF信号がありますが、これを非線形回路に入力したとき、いくつかの和と差のスペクトルが出力されます。そのうちの一つが、復調信号であるという考え方です。この場合、入力インピーダンスは、両側帯波別に求められ、4端子回路網で表現可能な形式に変換できるという寸法です。VSB検波などに威力を発揮しているようでした。(まだまだ理解不足なので続きは別途・・・)
9 主要参考文献
- [1]奥井重彦."電子通信工学のための特殊関数とその応用",1997,森北出版
- [2]Abramowitz and Stegun,"Handbook of Mathematical Functions"
- [3]後藤憲一,山崎修一郎."詳解 電磁気学演習" .1970. 共立出版
- [4]F.W.Grover."Inductance Calculations" .1973. Dover Publications
- [5]電気学会."電気磁気学" 1979.オーム社
- [6]古谷恒雄."空中線系および電波伝搬 空中線・伝送回路" .1971. 啓学出版
- [7]岡本次雄(JA1CA)."アマチュアのアンテナ設計法" .1996. CQ出版
- [8]小西良弘."無線通信回路入門講座" .1995. 総合電子出版
- [9] S.Loyka."Simple Formula for AM-detector transfer factor",Electronics
Letters, vol.35, No.2, pp.126-127, Jan. 1999.
- [10]提坂秀樹,大庭英雄."テキストブック無線通信機器".1991,日本理工出版.
- [11]川上正光."電子回路Ⅲ".1955.共立出版.
- [12]JIS C6102-1"AM/FM放送受信機試験方法第1部:一般的事項及び可聴周波測定を含む試験".1998.
ゲルマラジオの一つの特徴は、無数の構成が考えられることです。アンテナからレシーバに至るまで多種多様な組み合わせがあり、加えて、一つの構成要素の性能が全体に大きな影響を与える可能性が高いのです。
増幅素子を有するラジオ受信機では、不確定要素を抑える設計が容易ですが、ゲルマラジオは一要素が全体と密接に影響しあっているため、性能に影響する要素を一つづつ検討する必要があると思われます。
不確定要素をなるべく抑制するために、広く一般に用いられる方法の中から計算が容易となる組み合わせを選び、標準構成を決定することとしました。
アンテナは実際の使用状況と計算の容易さから、ループアンテナを想定します。個人が中波帯の実用アンテナとして数十mを超える「垂直アンテナ」を使用するのは困難ですし、水平部が長いアンテナは垂直偏波が伝搬の主である中波帯の環境下では簡易計算が困難です。
ループアンテナであれば測定器に用いられるほど感度が正確に計算でき[6]、アースが不要であることも不確定要素を減らすのに有効と考えました。
ループは室内でも使用可能な範囲で、製作の簡便さを考慮し、正方形で1辺の長さが50cm、直径0.6mmの銅の単線を仮定します。
同調回路はループアンテナのインダクタンスを利用してアンテナと兼用する一般的な方法を採用しました。当面は計算を簡略化するためタップまたはピックアップコイルは考慮せず、アンテナ回路と検波回路を直結する構成とします。
検波回路はごく標準的な包絡線検波回路とし、ダイオードの逆方向飽和電流を1μA、負荷抵抗を10kΩと設定しました。特に逆方向飽和電流は使用するダイオードの特性や周囲温度によって数桁異なるほど変動しやすく最大の不確定要素となりえます。
ここでは測定に使用したサンプル(1SS108の実測値3.2μA、1N60の実測値0.8μA)を考慮し、ばらつきが1桁のオーダであると見て1μAと設定することに決めました。無論その他の値もシミュレーションを実施し影響を考慮する必要があります。
なお、負荷抵抗Rは受話器そのものであるとみなして10kΩとしています。この値は通常100kΩ以上が用いられることが多く(おそらく、ロッシェル塩タイプのクリスタルイヤホンを想定した値)、それと比較して、かなり低い値ではあるのですが、レシーバのインピーダンス実測結果を考慮すると、この値のオーダが適当であると考えられます。
必要に応じて低周波トランスを用いてインピーダンス変換も可能ですが、それは別の機会に検討しましょう。fig.1に出来上がった標準ゲルマラジオの構成を示します。

fig1.標準ゲルマラジオの構成図

fig2. 正方形ループアンテナ
fig2に示した1回巻き正方形ループアンテナのインダクタンスL1は \[ L_1 = 0.8a \left( \ln \frac{2a}{r}-1.467 \right) \ [\mu H] \tag{4.1} \] で計算できます[3]。
ここでa[m]は1辺の長さ、r[m]は導線の半径です。a=0.5[m]、r=0.3[mm]としたときのインダクタンスL1は2.66[uH]になります。
このアンテナをそのまま同調回路の一部として使用するためには、市販バリコンの容量制限から300uH前後のインダクタンスが必要となるので、2.66uHのままでは大幅に不足してしまいます。そのためインダクタンスを増加させるには巻き数Nを増やして使用することになるのですが、N回巻きのインダクタンスLNは、 \[ L_N \simeq N^2 L_1 \tag{4.2} \] であり、巻き数の2乗に比例して増加します。(厳密には幅を考慮しない式のため、実際には式(4.1)よりインダクタンスが低下します。)
LN=330uHとするときのNを求めると、 \[ N = \sqrt{\frac{L_N}{L_1}} = \sqrt{\frac{330}{2.66}} = 11.14 \tag{4.3} \] であるので、巻き数は11回が適当となります。このときのインダクタンスは、L11=322uHとなり、同調回路に適した値となりました。
(※本節の計算は簡易的なものであり、より詳細なインダクタンスの計算[4]については、別途紹介する予定です。)
ループアンテナの直流抵抗RDCは、 \[ R_{DC} = \rho \frac{l_w}{\pi r^2} \tag{4.4} \] で計算できます。ここで、ρは導線の体積抵抗率、lwは導線の全長、rは(円形断面の)導線半径です。銅線の全長lwは \[ l_w = 4aN = 4 \times 0.5 \times 11 = 22 \ \mathrm{[m]} \tag{4.5} \] ですので、銅の体積抵抗率ρ=1.8×10-8 [Ω・m]、銅線半径r=0.3[mm]を式(3.4)に代入すると、 \[ R_{DC} = \frac{1.8 \times 10^{-8} \times 22}{3.141 \times (3 \times 10^{-4})^2} = 1.40 \ \mathrm{[\Omega]} \] が得られました。
この直流抵抗RDCは考え得る最小の抵抗値であって、高周波領域ではそのまま適用ができません。交流に対する効果の影響により非常に抵抗値が大きくなります。 適用条件を吟味する必要があります。
導線に高周波電流が流れる際、表面に電流が集中する現象が生じるため、高周波抵抗は直流に比べて大きくなる「表皮効果」が現れます。電流が内部に流れることができないために実効的な電線面積が減少してしまうのが原因です。(本質的に表皮効果を避けることは不可能ですが、リッツ線などの特殊電線を使用することで高周波抵抗を減少させることは可能)。
電線に高周波電流が流れた時、電流密度が電線表面の電流密度に比べて1/e=37%に減少する皮の厚さ(表皮深さ)をδとすると、 、μを銅線の透磁率、σを導電率として、 \[ \delta = \sqrt{\frac{2}{\omega \mu \sigma}} \tag{4.6} \] となります。
もし、導体の材質を電気銅(1/58[S/m] =1.72[Ω・m])とすれば、 \[ \delta \ \mathrm{[mm]} \simeq 0.0661 \sqrt{\frac{1}{f \mathrm{[MHz]}}} \tag{4.7} \] となり、周波数が1[MHz]であれば、δ=66[um]と計算できます。使用銅線の半径が0.3mm=300[um]ですから、実効面積が半減していることがわかります。
実際の高周波電流の分布は中心に向かって指数関数的分布になっているのですが、表面からδだけの範囲に一定の電流密度で流れているのと同等に扱うことができるので、 高周波抵抗RHFを求めるには表皮の面積Sを求めるだけでよいです。

fig3. 導線の断面図(表皮効果)
よって、電流が均等に流れていると仮定した領域の面積Sを求めてみると、 \begin{eqnarray} S & = & \pi(r^2-(r-\delta)^2) \\ & = & \pi(2 \delta r - \delta^2) \\ & \simeq & 2 \pi \delta r, \ \ (\delta \ll r) \tag{4.7} \end{eqnarray} となります。
δ=0.07[mm],r=0.3[mm}を代入すれば、面積S=1.32 ×10-7 [m2]となり、高周波抵抗RHFは=3.0[Ω] となりました (もう少し精度良く計算して3.4Ω程度)。ただし、実際の抵抗は表面抵抗の状態、近接効果などにより増加するため、余裕をみて、RHF=5[Ω]に設定することにします。(これでも結構低めの想定です。)
アンテナを電界強度Eの場に設置したとき、無負荷のアンテナに誘起する電圧をVoとすると、その比 \[ h_e = \frac{V_o}{E} \tag{4.8} \] を実効長または実効高と呼びます。仮想的なアンテナの長さで単位は[m]で表します。
最初に想定した微小ループアンテナの実効長heは、Nを巻き数、Aをループ面積、λを波長とすれば \[ h_e = \frac{2 \pi N A}{\lambda} \tag{4.9} \] と理論的にもシンプルとなります[5]
4.1節の結果から、N=11[回]、A=0.52=0.25[m2]、λ=300/f[MHz]=300[m]を代入すれば、実効長heは、 \begin{eqnarray} h_e &=& \frac{6.282 \times 11 \times 0.5^2}{300} \\ &=& 57.6 \times 10^{-3} \mathrm{[m]} \tag{4.10} \end{eqnarray} となり、5.76cmとなりました。
この程度の実効長は、同一条件での1/4波長垂直接地アンテナ(高さ75m)の実効高48[m]と比較すると、約800分の1という極めて小さい値になることが分かります。 要は標準アンテナと比較して感度が悪いと言う意味なのですが、AMラジオ帯域ではサイズ的にこれでも大きいアンテナの部類でもあり、いかに放送波が強力であるか を実感することができます。
なお、厳密にいえば実効長が小さくとも受信感度が劣ることを意味しません。ですが一般には、そのようなアンテナから電力を取り出すのは難しいため、低効率になりがちです。
以上の結果を等価回路として表すとfig.4となります。

fig4. アンテナ等価回路
5.1 同調容量
アンテナのインダクタンスLが求められているので、その同調容量Ctは \[ C_t = \frac{1}{\omega ^2 L} = \frac{1}{4 \pi^2 f^2 L} \ \mathrm{[F]} \tag{5.1} \] となるので、L=322[uH]、f=1[MHz]を代入して、Ct=79[pF]となります。
5.2 同調時の無負荷Qと等価回路

fig5. アンテナ及び同調回路の等価回路
図5はアンテナにキャパシタCtを接続して共振回路としたときの等価回路です。図5において、LとCtは電圧源側から見て直列共振しているため、 インピーダンスは0です。すなわち回路インピーダンスはRHFのみとなるため、その回路電流Iは \[ I = \frac{V_o}{R_{HF}} \tag{5.2} \] と計算されます。
その電流によって、端子1-1'に誘起される電圧をVsoとすると、Ctの持つインピーダンスと電流Iとの積になるので、 \[ V_{so} = \frac{I}{j \omega C_t} = -j \frac{V_o}{\omega C_t R_{HF}} \tag{5.3} \]
Vsoは通常、共振回路の性質によりVoよりも高い電圧となるので、その電圧上昇比をQoとすると式(5.3)より \[ Q_o = \frac{1}{j \omega C_t} \tag{5.4} \] とまとめられて、Vsoは \[ V_{so} = -j Q_o V_o \tag{5.5} \] とも表すことができます。
このQoは共振回路の無負荷Qと呼ばれる量です。(Qには単位がありません)式の中の"-j"はVoとの位相差が90度であることを表すだけなので、ゲルマラジオ用としては無くても支障が無いパラメータです。そのため、以降は絶対値だけを扱うことにします。
式(5.4)に、Ct=79[pF] 、f=1[MHz] 、RHF=5[Ω]を代入すると、Qo=405となって、端子1-1'にはアンテナ誘起電圧Voの405倍もの共振電圧が生じることを示しています。
現実にはキャパシタの損失分や経験値などから、もう少し小さくなる(100~200)はずですが、ここでは損失がRHFのみとして仮計算しておきます。
5.3 回路の直並列変換
(5.4)節では、共振回路に何も接続しない無負荷の状態を計算していますが、実際には検波回路が負荷となるため、これを影響に入れなくてはなりません。そのため、負荷を接続したときに計算がしやすいよう、直並列変換を行います。

fig.6 等価回路の直並列変換
fig.6 の左側が、前節での等価回路に相当します。端子1-1'から見たインピーダンスは、電圧源を短絡すればいいわけです。ここで、直列抵抗RHFの影響を、fig.6 左側の並列抵抗Rpに等価変換するためには、 \[ R_p = \frac{\omega ^2 L^2 }{R_{HF}} \tag{5.6} \] とします。(ただし、直列抵抗RHFがLのインダクタンスに比べて十分小さいという仮定の元に変換が行われているため、RHFが極端に大きい回路では成立しないことに注意する必要があります。)
回路は共振状態ですので、$X_L = \omega L = 1/\omega C $が成立しているために、以下のようにも変換が可能です。 \begin{eqnarray} R_p &=& \frac{\omega ^2 L^2 }{R_{HF}} \\ &=& \frac{1}{\omega ^2 C_t^2 R_{HF}} \\ &=& \frac{1}{R_{HF}} \cdot \frac{L}{C_t} \\ &=& X_L Q_o \tag{5.7} \end{eqnarray}
式(5.7)に、ω=6.28×106[rad/s]、Ct=79[pF]、RHF=5[Ω]を入れると、Rp=819[kΩ]なる並列抵抗値が得られます。これは共振回路のインピーダンスに相当する量です。
単純には、共振時のLまたはCのリアクタンスがQ倍されたと考えると分かりやすく、Qが高いほどRpも高くなる寸法です。
5.4 電流源の計算
図6の等価回路には電源が無いままですので、これに電流源を付加したのが図7です。

fig.7 電流源のあるアンテナ-同調回路の等価回路
電流源Iの値を求めるには、1-1'間の電圧がVsoであることと、式(5.3)(5.7)を利用します。回路は共振状態にあるので、電流は全てRpに流れるとみなしてもよく \begin{eqnarray} I &=& \frac{V_{so}}{R_p} \\ &=& \frac{V_o}{\omega C_t R_{HF}} \cdot \omega ^2 C_t^2 R_{HF} \\ &=& \omega C_t V_o \tag{5.8} \end{eqnarray} と、簡単な結果になりました。
5.5 負荷接続時のアンテナ-同調回路
アンテナ-同調回路の最後の計算目的は、負荷Ziを接続したときの1-1'間の電圧Vslを求めることにあります。(記号をZiとしたのは、検波回路の"入力インピーダンス"が負荷となるからです。またVslはV source loadの意。)
負荷を接続したときの等価回路を図8に示します。

fig.8 負荷接続時のアンテナ-同調回路の等価回路
等価共振回路インピーダンスRp、負荷Ziに流れる電流をそれぞれIR、IZとおくと、 \[ I = \frac{V_{sl}}{I_R} + \frac{V_{sl}}{I_Z} \tag{5.9} \] 。式(5.8)より$ I=\omega C_t V_o $であるので、式(5.9)に代入して \[ V_{sl} \left( \frac{1}{R_p} + \frac{1}{Z_i} \right) = \omega C_t V_o \tag{5.10} \] 。式(5.10)をVslについて解くと \begin{eqnarray} V_{sl} & = & \cfrac{\omega C_t V_o}{\omega ^2 C_t^2 R_{HF} +\cfrac{1}{Z_i}} \\ & = & \cfrac{V_o}{\omega C_t R_{HF} + \cfrac{1}{Z_i}} \\ & = & \cfrac{V_o}{\cfrac{1}{Q_o}+\cfrac{1}{\omega C_t Z_i}} \tag{5.11} \end{eqnarray}
ここで、式(5.11)の中にある、$ \omega C_t Z_i $なる量は、無損失の共振回路の負荷としてZiのみが接続されているときのQに相当する量です。 すなわち \[ Q_z = \omega C_t Z_i \tag{5.12} \] として、Qoの仲間として扱うとき、この量を「外部Q」と呼びます[8]。
式(5.11)を式(5.12)を利用して書き直せば、 \[ V_{sl} = \cfrac{V_o}{\cfrac{1}{Q_o}+\cfrac{1}{Q_z}} = Q_L V_o \tag{5.13} \] と、非常に見通しよくまとめられます。
ここで、QLは負荷Qとか実効Qと呼ばれる量です。式(5.13)をみると、負荷Qは並列抵抗を求めるときと同様の形を取っていることが分かります。すなわち、外部Q、無負荷Qをそれぞれ抵抗とみなしたとき、その並列抵抗の値を求めると負荷Qの値と一致するのです。このことはQを考える際に非常に役立ちます。
(補足:Qが並列抵抗と同様に求められるのは、裏で実際に並列抵抗を求める操作をしているからなのです。)
一例として、Zi=50[kΩ]の負荷を接続したときのQを求めてます。この負荷は一般に十分大きな抵抗であるとみなせるのですが、キンキンに共振している共振回路にとっては重い負荷となり、外部QはわずかにQz=25です。結果、負荷QはQL=23にまで低下してしまいます。前提としている無負荷Qが$Q_o=405$という大きな値でありながら、事実上、外部Qが負荷Qを決定してしまうのです。
よって、ゲルマラジオの同調回路の設計においては、負荷Qを意識しながら進めなくてはならないことがわかります。
5.6 アンテナ-同調回路のまとめ
負荷Ziの検波回路を接続したときの、アンテナ-同調回路の出力電圧Vslは \begin{eqnarray} V_{sl} & = & Q_L V_o \tag{5.13} \\ V_o & = & E h_e = 2 \pi NAE/\lambda \tag{4.9} \\ Q_L & = & \cfrac{1}{\cfrac{1}{Q_o}+\cfrac{1}{Q_z}} \tag{5.13} \\ Q_o & = & \frac{1}{\omega C_t R_{HF}} \tag{5.4} \\ Q_z & = & \omega C_t Z_i \tag{5.12} \end{eqnarray}
ここで、
- $V_{sl}$
- 負荷(検波器)接続時の同調回路共振電圧[V]
- $V_o$
- 無負荷時のアンテナ誘起電圧[V]
- $Q_L$
- 同調回路の負荷Q
- $Q_o$
- 同調回路の無負荷Q
- $Q_z$
- 同調回路の外部Q
- $\omega$
- 角周波数$=2 \pi f \ \mathrm{[rad/s]}$
- $C_t$
- 同調回路の静電容量[F]
- $Z_i$
- 負荷(検波器)の入力インピーダンス[Ω]
- $N$
- ループアンテナの巻き数
- $A$
- ループアンテナの面積[m2]
- $E$
- 受信点の電界強度[V/m]
- $\lambda$
- 受信波長[m]
- $h_e$
- アンテナの実効長[m]
本節までの計算で、電界強度と負荷インピーダンス、及び同調回路共振電圧の関係が求められました。
6 検波回路
6.1 検波回路の入出力特性

fig.9 包絡線検波回路
fig.9に示す包絡線検波回路の出力電圧Eoは、別ページで導出したとおり、 \begin{eqnarray} E_o &=& V_T \ln \left[ \mathrm{I_0} \left(\frac{E_m}{V_T} \right) \right] \\ && \ \ \ - V_T \left( 1 + \frac{E_o}{R I_s}\right) \tag{6.1} \end{eqnarray} です。ここで各変数は、
- $E_o$
- 出力電圧 [V]
- $E_m$
- 入力交流振幅[V]
- $V_T$
- ダイオードの熱電圧 $=kT/q \simeq 26\mathrm{[mV]}$@室温。
- $R$
- 負荷抵抗[Ω]
- $I_s$
- ダイオードの逆方向飽和電流 [A]
- $\mathrm{I_0}(x)$
- 第1種0次変形ベッセル関数
- $\mathrm{I_1}(x)$
- 第1種1次変形ベッセル関数
- $\ln(x)$
- 自然対数
式(6.1)は特殊な条件を与えない限り解析的には解くことができず、近似式(Loyka式[9])を用いても、ゲルマラジオの感度を求めるには最も精度の悪い(最大で40%弱)範囲にあたるため、手計算はちょっと難しそうです。このような場合は、Newton-Raphson法を用いてシミュレーションを行うしかなさそうです。
26mV以下の小信号領域や、1V以上での大信号領域では近似式が使用できるのですが、ゲルマラジオで使用する領域では高精度の近似式が見当たらないのが現状です。以下の議論は、入出力特性グラフが計算できることを前提に進めることにします。
6.2 所要出力を得るのに必要な入力電圧
結論から先に書くと、出力信号電圧の振幅が10mVとなるためには、80[mV]の入力振幅が必要でした。これはシミュレーションを行った結果なのですが、以下に基本的な考えかたを記載します。
まず、検波効率をηとしたときに、その定義より \[ E_o = \eta E_m \tag{6.2} \] が成り立ちます。
ここで、Emは入力RF信号の振幅を表していますが、AM変調波はEmを変化させる変調方式であるので、時間的に変動するパラメータになります。 これを式で示すと、 \[ E_m = E_c (1+ m \cos (pt)) \tag{6.3} \] です[10]。ここで、Ecは搬送波振幅、mは変調度(0.3を仮定)、pは変調波の角周波数を表します。
次に、Isを1[uA]、R=10[kΩ]にしたときの検波特性グラフを図10-1に示します。
fig.10-1を見ると、100mV以下のEm入力範囲では、検波効率ηが直線であることから、ほぼ2乗特性であることが分かります。この範囲では入力が2倍になると、出力が4倍となる性質があります。
次の図10-2はEm=300mVまでの範囲について、入出力微分特性を描いたものです。これを見ると約150mV以下であれば、ほぼEmに比例した直線であり2乗特性としてみなせそうです。
(補足:微分値の傾きがEmに1次比例するということは、2乗特性であることを意味します。もし、微分値の傾きが水平ならば線形(直線検波)特性であることが分かります。)
300mV以上のRF入力だとほぼ直線検波領域となっていますが、今求めるべきものは小信号領域での感度ですので、全体を2乗特性として扱うことにします。すなわち、 kを比例定数として \[ E_o = k E_m^2 \tag{6.4} \] と仮定するわけです。
式(6.2)と式(6.4)の関係から \[ \eta = k E_c \tag{6.5} \] また、式(6.4)に式(6.3)を代入すると復調信号Eom(om:output, modulated)が計算できて、 \begin{eqnarray} E_{om} & = & k E_m^2 \\ &=& k E_c^2 (1 + m \cos(pt))^2 \\ &=& k E_c^2 (1 + 2m \cos pt + m^2 \cos^2 pt) \\ &=& k E_c^2 \left(1 + 2m \cos pt + m^2 \frac{1+\cos 2pt}{2} \right) \end{eqnarray} 整理して、 \begin{eqnarray} E_{om} &=& \left(1 + \frac{m^2}{2} \right) k E_c^2 \\ && \ \ + 2 k m E_c^2 \cos pt \\ && \ \ \ \ + \frac{1}{2} m^2 k E_c^2 \cos 2pt \tag{6.6} \end{eqnarray}
一方、無変調時(m=0)のときの出力電圧をEonとすれば(on:output, non-modulated)、 \[ E_{on} = k E_c^2 = \eta E_c \tag{6.7} \] になります。
式(6.6)の復調出力を、直流成分VDC、目的信号(復調成分)vs、目的外の成分(歪み)vdstに分類すると \begin{eqnarray} V_{DC} & = & k E_c^2 (1+m^2/2) \tag{6.8} \\ v_s & = & 2 k m E_c^2 \cos(pt) \tag{6.9} \\ v_{dst}& = & \frac{1}{2} k m^2 E_c^2 \cos (2pt) \tag{6.10} \end{eqnarray} となります。
AM復調された信号は、目的とする信号波成分以外に、歪みを原因とする直流成分(m2/2)がDC成分に加わり、また第2高調波(cos2pt)成分が生じているのです。 特に、この歪み成分vdstは、2乗検波の悪い特徴です。歪み率はm/4で、100%変調時(例えば、音楽放送時のピーク値など)では最高25%にもなります。
さて、ここで目的とする復調波vsに注目すると \begin{eqnarray} v_s &=& 2m(k E_c)E_c \cos pt \\ &=& 2 m \eta E_c \cos pt \tag{6.11} \end{eqnarray} と変形できて、直線検波時の倍の出力が得られていることも分かります。これも2乗検波の特徴です。
よって、信号波の振幅を \[ V_s = 2m \eta E_c \tag{6.12} \] とおき、これを次のように式変形します。 \[ \eta E_c = \frac{V_s}{2m} \tag{6.13} \]
式(6.13)は、式(6.7)を使うと、最終的に \[ E_{on} = \frac{V_s}{2m} \tag{6.14} \] と表すことができます。式(6.14)は復調信号の振幅値Vsと無変調時の出力DC電圧値VDCを関係づける重要な式です。
式(6.14)に必要とする復調信号電圧振幅Vsと変調度mを与えてやれば、無変調時の出力DC電圧が計算できて、fig.10-1から入力搬送波振幅Emが求められるのです。
実際に計算をすると、Vs=10[mV]、m=0.3から、Eon=17.1[mV]が得られました。この出力を得るのに必要な入力搬送波振幅は、グラフ図10-1より、Ec=80[mV]と求められます。すなわち、10mVの復調出力振幅を得るには、80mVの入力RF振幅が必要であることが分かりました。fig.11にその手順の一部を示します。
6.3 入力等価抵抗
検波器の入力等価抵抗Refは、入力実効値を2乗して、その回路消費電力で割って定義される値です。(ef:effectiveの意味)。振幅の場合は実効値に換算するために、さらに2で割る必要があります。 \[ R_{ef}=\frac{E_m^2}{2P} \] 詳細は付録2にて紹介してありますが、ここでは結果だけを書くことにします。 \[ R_{ef} = \frac{1}{2} \cdot \cfrac{E_m}{I_s + \cfrac{E_o}{R}} \cdot \frac{\mathrm{I_0}(E_m/V_T)}{\mathrm{I_1}(E_m/V_T)} \tag{6.15} \] ここで、
- $E_o$
- 出力電圧 [V]
- $E_m$
- 入力交流振幅[V]
- $V_T$
- ダイオードの熱電圧 $=kT/q \simeq 26\mathrm{[mV]}$@室温。
- $R$
- 負荷抵抗[Ω]
- $I_s$
- ダイオードの逆方向飽和電流 [A]
- $\mathrm{I_0}(x)$
- 第1種0次変形ベッセル関数
- $\mathrm{I_1}(x)$
- 第1種1次変形ベッセル関数
かなり複雑な関数で、変形ベッセル関数という特殊関数も入っています。解析解が非常に求めにくいので、数値計算シミュレーションするしか方法が見つかりません。ですが、いくつかの信号レベルに分けると、近似値が得られるので、その結果を以下に記します。
まず小信号の極限は、 \[ \lim_{E_m \to 0} R_{ef} = \frac{V_T}{I_s} \tag{6.16} \] に収束し、大信号の極限(少なくとも1V以上)は \[ \lim_{E_m \to \infty} R_{ef} = \frac{R}{2} \tag{6.17} \] に漸近します。これは式(3.46)の結果は線形近似理論[10][11]と一致しています。
その中間の領域では、検波効率$\eta = E_o/E_m$を用いて近似的に \[ R_{ef} = \frac{R}{2\eta} \tag{6.18} \] となり、検波効率が高いときには良い一致を示しました。ですが、小信号領域では比較的誤差が大きいため、数値シミュレーションしたグラフより、等価抵抗を求めることにします。
fig.12に式(6.15)のシミュレーション結果を示します。青線がシミュレーション結果、赤線が式(6.18)の近似式です。
グラフより、入力80[mV]のときの入力等価抵抗は18k[Ω]と求められました。(※実際には振幅変調であるために、 時間によって、インピーダンスが変化します。また、負荷となるコンデンサCは、復調信号が交流であるために、多少なりとも影響が出ます。 もう少し詳細な議論が必要になりそうです。実際、参照した論文の中にはこのキャパシタを含んだ負荷の複素インピーダンスが、 各サイドバンドに対して共役インピーダンスとして振舞うと記されています。)
7 感度の最終計算
前節までの計算によって、電界強度と同調回路の出力の関係、並びに所要出力を満たすための検波回路入力レベルとその入力等価抵抗が求められました。
これらの結果を組み合わせていけば、感度が求められるはずです。
7.1 検波器の外部Qと全体の負荷Q
式(5.12)に式(6.15)によって得られた値、Ref=18[kΩ]を代入すると、外部Qは \begin{eqnarray} Q_z &=& \omega C_t Z_i \\ &=& 6.282 \times 10^6 \times 79 \times 10^{-12} \times 18 \times 10^3 \\ &=& 8.9 \end{eqnarray}
これと、無負荷時のQo=405を式(5.13)に代入して、 \begin{eqnarray} Q_L &=& \cfrac{1}{\cfrac{1}{Q_o}+\cfrac{1}{Q_z}} \\ &=& \cfrac{1}{\cfrac{1}{405}+\cfrac{1}{8.9}} \\ &=& 8.7 \tag{7.2} \end{eqnarray}
すなわち、検波器を接続した状態での共振回路のQは8.7まで低下することになります。
7.2 感度の最終計算
同調回路の出力電圧式(5.13)と、電界強度Eアンテナ誘起電圧の関係式(4.9)をまとめ、Eについて解くと、 \[ E = \frac{V_{sl}}{Q_L h_e} \tag{7.3} \]
ここに、Vsl=80[mV]、QL=8.7、he=5.76[cm]を代入すると \[ E = \frac{0.08}{8.74 \times 0.0576} = 0.16 \mathrm{[V/m]} \tag{7.4} \] となり、これにてようやく標準ゲルマラジオの感度が160[mV/m]であることが求められました。
7.3 補足
(7.2)節で算出された感度は、数桁外れの誤差を生じていないことぐらいは分かりますが、直感的にはやや低い印象を受けます。
これは、同調回路と検波器を直結することによるミスマッチに起因する問題のようです。もし、タップを用いるなどして、インピーダンスを適切に設定した場合には、E=46mV/m、QL=202が得られました。
なお、タップが理想トランスのように働くと仮定して、タップを2巻き目の位置にとった場合には、 E=47[mV/m]、QL=162となり、もう少しは高感度化が可能である見通しも得られました。
これらは、アンテナの性能によって大きく変わるところでもあり、受信機としてのコア部分、レシーバの部分、アンテナ部分をもう少し分離して整理することが課題です。 一つのパーツが、例えばイヤホンそのものが、アンテナまでに影響するというのが難しさを著しくしていると思います。
別ページにて、一般的なゲルマ受信機部分の実測結果によれば、キャリア基準で-33dBm程度が受信限界となりました。 他方、今回の受信機基準では、キャリア振幅Ec=80mV、検波器の入力Z=18[Ω]から計算して、-37.5dBm程度を想定しています。
受信機はおおむね同程度の感度なので、あと数dB程度の改善ができるとうれしく、アンテナの方は幾らでも工夫の余地ありというところでしょうか。
8 感想など・・・
たかがゲルマラジオとはいえ、理論的な壁-特に検波器-は非常に厚く、ここまで概算を求めるまで約1年を要しました。しかし、実験も検討もまだ緒についたところ。ようやく一里塚に達したようなものです。ゲルマラジオには、まだまだ未知の領域が隠されているように見えてなりません。
それと、上記の議論は時間領域での計算しかしていませんが、古い論文を見ると、包絡線検波器はTVが普及した時期に数多くの伝達関数を求める研究が進められたようで、「周波数変換器としてのダイオード検波器」という手法を目にした時は思わず唸ってしまいました。目からうろこです。
AMスペクトルを見ると、両側波帯を伴ったRF信号がありますが、これを非線形回路に入力したとき、いくつかの和と差のスペクトルが出力されます。そのうちの一つが、復調信号であるという考え方です。この場合、入力インピーダンスは、両側帯波別に求められ、4端子回路網で表現可能な形式に変換できるという寸法です。VSB検波などに威力を発揮しているようでした。(まだまだ理解不足なので続きは別途・・・)
9 主要参考文献
- [1]奥井重彦."電子通信工学のための特殊関数とその応用",1997,森北出版
- [2]Abramowitz and Stegun,"Handbook of Mathematical Functions"
- [3]後藤憲一,山崎修一郎."詳解 電磁気学演習" .1970. 共立出版
- [4]F.W.Grover."Inductance Calculations" .1973. Dover Publications
- [5]電気学会."電気磁気学" 1979.オーム社
- [6]古谷恒雄."空中線系および電波伝搬 空中線・伝送回路" .1971. 啓学出版
- [7]岡本次雄(JA1CA)."アマチュアのアンテナ設計法" .1996. CQ出版
- [8]小西良弘."無線通信回路入門講座" .1995. 総合電子出版
- [9] S.Loyka."Simple Formula for AM-detector transfer factor",Electronics
Letters, vol.35, No.2, pp.126-127, Jan. 1999.
- [10]提坂秀樹,大庭英雄."テキストブック無線通信機器".1991,日本理工出版.
- [11]川上正光."電子回路Ⅲ".1955.共立出版.
- [12]JIS C6102-1"AM/FM放送受信機試験方法第1部:一般的事項及び可聴周波測定を含む試験".1998.
たかがゲルマラジオとはいえ、理論的な壁-特に検波器-は非常に厚く、ここまで概算を求めるまで約1年を要しました。しかし、実験も検討もまだ緒についたところ。ようやく一里塚に達したようなものです。ゲルマラジオには、まだまだ未知の領域が隠されているように見えてなりません。
それと、上記の議論は時間領域での計算しかしていませんが、古い論文を見ると、包絡線検波器はTVが普及した時期に数多くの伝達関数を求める研究が進められたようで、「周波数変換器としてのダイオード検波器」という手法を目にした時は思わず唸ってしまいました。目からうろこです。
AMスペクトルを見ると、両側波帯を伴ったRF信号がありますが、これを非線形回路に入力したとき、いくつかの和と差のスペクトルが出力されます。そのうちの一つが、復調信号であるという考え方です。この場合、入力インピーダンスは、両側帯波別に求められ、4端子回路網で表現可能な形式に変換できるという寸法です。VSB検波などに威力を発揮しているようでした。(まだまだ理解不足なので続きは別途・・・)
- [1]奥井重彦."電子通信工学のための特殊関数とその応用",1997,森北出版
- [2]Abramowitz and Stegun,"Handbook of Mathematical Functions"
- [3]後藤憲一,山崎修一郎."詳解 電磁気学演習" .1970. 共立出版
- [4]F.W.Grover."Inductance Calculations" .1973. Dover Publications
- [5]電気学会."電気磁気学" 1979.オーム社
- [6]古谷恒雄."空中線系および電波伝搬 空中線・伝送回路" .1971. 啓学出版
- [7]岡本次雄(JA1CA)."アマチュアのアンテナ設計法" .1996. CQ出版
- [8]小西良弘."無線通信回路入門講座" .1995. 総合電子出版
- [9] S.Loyka."Simple Formula for AM-detector transfer factor",Electronics Letters, vol.35, No.2, pp.126-127, Jan. 1999.
- [10]提坂秀樹,大庭英雄."テキストブック無線通信機器".1991,日本理工出版.
- [11]川上正光."電子回路Ⅲ".1955.共立出版.
- [12]JIS C6102-1"AM/FM放送受信機試験方法第1部:一般的事項及び可聴周波測定を含む試験".1998.