（付録２）
検波器の入力インピーダンス

厳密式の導出過程

本ページは検波器の入力インピーダンスの補足資料です。 \[ Z_{in} = \frac{V_c}{2(I_s+ I_{dc})} \cdot \frac{f_0(V_c/V_T)}{f_1(V_c/V_T)} \] の導出過程について問い合わせがあったため作成したものです。

本式は、ダイオード特性を本来の指数関数特性のまま解いたものですが、この辺りを参考にできる教科書や論文が見当たらないので、自力で導出したものです。（よって、参考文献はありませんのであしからず。）

解析するモデル

単純な、図１の回路を対象とします。

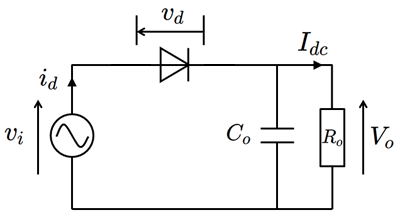
図１.解析対象の回路モデル

前提として、静電容量Ｃｏは十分に大きく、入力周波数に対して短絡状態とみなせると仮定します。またダイオード特性は内部抵抗成分を考慮せず、ダイオード電流式(1)に従うとします。 \[ i_d = I_s \left(e^{v_d/V_T}-1 \right) \tag{1} \]

ここで、ここで、各記号は以下の通りです

$i_d$: ダイオード電流[A]
$I_s$: ダイオードの逆方向飽和電流[A]
$v_d$: ダイオードの両端電圧[V]
$V_T$: ダイオードの熱電圧[V]

ダイオード両端電圧

簡単のため、入力ＲＦ電圧$v_i$を、振幅$V_c$の正弦波とすれば、 \[ v_i= V_c \cos \theta \tag{2} \] と表現ができます。

すると、ダイオードの両端電圧$v_d$は出力ＤＣ電圧$V_o$と入力ＲＦ電圧$v_i$の差となるので、

\[ v_d = V_c \cos \theta - V_o \tag{3} \]

ダイオードを流れる電流

ダイオードを流れる電流$i_d$は、式(1)に式(3)を代入して、

\[ i_d = I_s \left[ \exp \left(\frac{V_c \cos \theta - V_o}{V_T}\right) -1\right] \tag{4} \] となります。

ダイオードを流れる直流電流

ダイオードを流れるDC電流は、式(4)を積分して時間平均をとることで求められます。交流一周期の平均電流は、 \[ I_{dc} = \frac{1}{2\pi} \int^{\pi}_{-\pi} i_d \ d\theta \tag{5} \] です。

式(5)の積分過程を示せば、

\begin{eqnarray} I_{dc} &=& \frac{Is}{2\pi} \int^{\pi}_{-\pi} e^{\frac{V_c \cos \theta - V_o}{V_T}} d\theta -\frac{I_s}{2\pi} \int^{\pi}_{-\pi} d\theta \\ &=& I_s \ e^{-\frac{V_o}{V_T}} \frac{1}{2\pi} \int^{\pi}_{-\pi}e^{\frac{V_c}{V_T}\cos \theta} d\theta -I_s \\ &=& I_s \ e^{-\frac{V_o}{V_T}} \left[ \frac{1}{\pi} \int^{\pi}_{0} e^{\frac{V_c}{V_T} \cos \theta} d\theta \right] -I_s \\ &=& I_s \ e^{-\frac{V_o}{V_T}} \ f_0\left(\frac{V_c}{V_T}\right) -I_s \\ &=& I_s \left[ e^{-\frac{V_o}{V_T}} \ \ f_0\left(\frac{V_c}{V_T}\right) -1 \right] \tag{5-1} \end{eqnarray}

となって、最終的に

\[ I_{dc} = I_s \left[ e^{-\frac{V_o}{V_T}} \ \ f_0\left(\frac{V_c}{V_T}\right) -1 \right] \tag{6} \]

の結果が得られます。

途中で出てくる$f_0(x)$の関数は、第１種０次変形ベッセル関数です。通常は、この関数を$I_0(x)$と表記するのですが、電流の$I$記号と紛らわしいため、代替的に$f_0(x)$と表記したものです。

０次ベッセル関数$J_0(x)$と０次変形ベッセル関数の関係、及びその積分表示と級数展開は以下のとおりです。

\begin{eqnarray} J_0 (jx) = f_0 (x) &=& \frac{1}{\pi} \int_{0}^{\pi} e^{x \cos \theta} d \theta = \sum_{k=0}^{\infty} \frac{(x^2/4)^{k}}{(k!)^2} \tag{7} \end{eqnarray}

ダイオードを流れる高周波電流

入力の消費電力を求めるのが最終目的なのですが、そのためには高周波電流の量を求める必要があります。そこで式(6)で示されたダイオード電流の歪み波をフーリエ級数に展開して各高調波成分を求めていきます。

フーリエ級数で表すときのダイオード電流は、電流が$\theta=0$に対して偶関数なのでsin項は不要となりcos項のみでよいことから、

\begin{eqnarray} i_d &=& I_{dc} +I_1 \cos \theta +I_2 \cos 2\theta \\ && \ \ + I_3 \cos 3\theta + \cdots + I_n \cos n\theta + \cdots \tag{8} \end{eqnarray}

の形式で表すことができます。この中で直流分の$I_{dc}$は式(6)にて既に結果が得られています。

式(8)のn次の周波数成分の電流振幅$I_n$を求めれば、

\[ I_n = \frac{1}{\pi} \int^{\pi}_{-\pi} i_d \cos n\theta \ \ d\theta \tag{9} \]

となります。実際に式(9)に式(4)のダイオード電流を代入して計算すると、

\begin{eqnarray} I_n &=& \frac{1}{\pi} \int^{\pi}_{-\pi} i_d \cos n\theta \ \ d\theta \\ &=& \frac{I_s}{\pi} e^{-\frac{V_o}{V_T}} \int^{\pi}_{-\pi} e^{\frac{V_c}{V_T} \cos \theta} \cos n\theta d\theta - \frac{I_s}{\pi} \int^{\pi}_{-\pi} \cos n\theta \ \ d\theta \\ &=& 2 I_s e^{-\frac{V_o}{V_T}} \frac{1}{\pi} \int^{\pi}_{0} e^{\frac{V_c}{V_T} \cos \theta} \cos n\theta \\ &=& 2 I_s e^{-\frac{V_o}{V_T}} f_n \left(\frac{V_c}{V_T}\right) \tag{9-1} \end{eqnarray}

となり、最終的に \[ I_n = 2 I_s e^{-\frac{V_o}{V_T}} f_n \left(\frac{V_c}{V_T}\right) \tag{10} \] の結果が得られました。

ここで、$f_n$はｎ次の第１種変形ベッセル関数です。（変形ベッセル関数は$I_n(x)$で表すのが標準的であるが、電流の$I$記号と紛らわしいため、代替的に$f_n(x)$の表記とした。）。

ｎ次のベッセル関数$J_n(x)$およびｎ次の変形ベッセル関数$f_n(x)$との関係は以下の通りです。 \begin{eqnarray} f_n(x) &=& j^{-n} J_n(jx) \\ &=& \frac{1}{\pi} \int^{\pi}_{0} e^{x \cos \theta } \cos n\theta \ \ d\theta \\ &=& \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(x^2/4)^{k}}{(n+k)!k!} \tag{11} \end{eqnarray}

入力電力の計算

検波器への入力電力は、入力周波数における電圧振幅と電流振幅を掛けて２で割れば求められます。入力周波の電流振幅は式(13)より、 \[ I_1 = 2 I_s e^{-\frac{V_o}{V_T}} f_1 (V_c/V_T) \tag{12} \] であり、印加電圧と同一周波数の電流成分を$i_1$と表記して、 \[ i_1 = 2 I_s e^{-\frac{V_o}{V_T}} f_1 (V_c/V_T) \cos \omega t \tag{13} \] という正弦波電流になります。また、検波器への入力電圧振幅は式(2)で印加電圧として定義した値であって、 \[ v_1 = V_c \cos \omega t \tag{14} \] です。

入力側から見た消費電力$P_{in}$は、式(13)(14)の実効値を掛けたものになるので、

\[ P_{in} = \frac{V_c I_1}{2} = V_c I_s e^{-\frac{V_o}{V_T}} f_1(V_c/V_T) \tag{15} \]

となります。

ここで、式(6)より \[ e^{-\frac{V_o}{V_T}} = \frac{1+I_{dc}/I_s}{f_0 (V_c/V_T)} \tag{16} \] であることを考慮して式(15)に代入すると \[ P_{in} = V_c (I_s+I_{dc}) \frac{f_1(V_c/V_T)}{f_0(V_c/V_T)} \tag{17} \] が得られます。

この式(17)が、検波器が消費する電力です。

等価入力インピーダンスの計算

本ページの最終目的である検波器の等価入力インピーダンス$Z_{in}$は、 \[ Z_{in} = \frac{V_c^2}{2P_{in}} \tag{19} \] が定義となるため、式(17)を代入し、 \[ Z_{in} = \frac{V_c}{2(I_s+I_{dc})} \cdot \frac{f_0(V_c/V_T)}{f_1(V_c/V_T)} \tag{20} \] が得られます。

第１種ｎ次変形ベッセル関数の表記をこのページで使用している$f_n(x)$から、数学書で一般によく用いられる$I_n(x)$に戻すと、 \[ Z_{in} = \frac{V_c}{2(I_s+ I_{dc})} \cdot \frac{\mathrm{I_0}(V_c/V_T)}{\mathrm{I_1}(V_c/V_T)} \tag{21} \] という表記になりますが、電気回路なので電流っぽいＩを使うのは紛らわしく悩ましいところです。

また、本回路の前提条件では、直流電流値$I_{dc}$を抵抗$R_o$と出力DC電圧$V_o$で表現して、

\[ Z_{in} = \cfrac{V_c}{2 \left(I_s+ \cfrac{V_o}{R_o}\right)} \cdot \frac{f_0(V_c/V_T)}{f_1(V_c/V_T)} \tag{22} \]

と表現することもできます。

もし、十分大きな入力があって回路に十分な電流が流れている場合には、$I_s$が無視でき、かつ$f_0(x)$と$f_1(x)$がほぼ等しくなるので、式(22)は、 \begin{eqnarray} Z_{in} &\simeq& \frac{R_o V_c}{2 V_o} \\ & = & \frac{R_o}{2 \eta} \tag{23} \end{eqnarray} と近似でき、古典式や簡易式と結果が一致します。

さらに詳しい性質については別ページを準備中です。

（付録２）検波器の入力インピーダンス