クリスタルイヤホンを測定したい！

HOMEに戻る

写真１．クリスタルイヤホン

ゲルマラジオを鳴らすときには、必ずといっていいほどクリスタルイヤホンのお世話になりますね。

一言でクリスタルイヤホンとは言っても、ロッシェル塩タイプとセラミックタイプの二つがあります。普段手に入るのはセラミックタイプです。

￥３００前後と安価で入手性も良いですし、インピーダンスが高く、小さな電圧でも鳴ってくれる利便性にはお世話になりっぱなしです。

値段さえ気にしなければ、ハイ・インピーダンスのマグネチック型レシーバーを使ったり、普通のヘッドホンにトランスを付けて使う事もできますが、お手軽さやコストパフォーマンスはクリスタルイヤホンに及ばないでしょう。

ここでは、そんなクリスタルイヤホンの電気的特性について調べてみよう！というのが本ページの目的です。

ただし、ロッシェル塩タイプはそもそもが入手困難であり、私もサンプルを求めて駆け回りましたが入手に至りませんでしたので、セラミックイヤホンのみの測定であることをお断りいたします。

このイヤホン、先輩たちから様々な伝説が伝えられてきました。

• 湿気には気をつけろ！
• インピーダンスは無限大
• 電圧さえあれば動作する

しかし、湿気はロッシェル塩タイプに限ったものですし、電圧だけでも鳴るというのは、物理的に見てやや胡散臭いものです。

特にインピーダンスが無限大という部分については、理論的に見て明らかにおかしいのです。圧電素子であるクリスタルイヤホンは、絶対にインピーダンスが小さい「ハズ」です。

しかし、理論でグダグダいうものでもなく、この真偽を確かめるには実測した方が早そうです。

測定したいのはクリスタルイヤホンのインピーダンスです。

一番単純な方法は、イヤホンの静電容量を測定することでしょう。イヤホンは圧電素子型なため、一種のコンデンサとして作用するはずです。この静電容量Cからインピーダンスが求められるはずです。

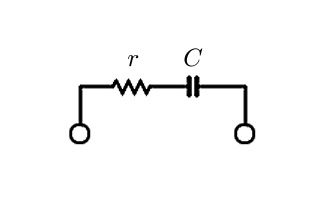
図１．単純な等価回路

最近は安物のテスターでも静電容量を測れるようになっていますので、これでとりえあず計ってみることにします。

C=20.4ｎF

あれ！？…測定間違ってる？！！…　何かの間違いかとも思いましたが、本当に0.02μFもの容量があることが分かりました。

こんな大容量のコンデンサを負荷にしていたとは驚きでした。

ゲルマラジオでは、負荷に100pF(=0.1nF)とかいう値を入れていますが、もはやこんな静電容量はゴミと言わんばかりのドでかい200倍もの静電容量だったのです。

クリスタルイヤホンを使う時は、検波回路にコンデンサは不要かもしれません。こんなに大容量な負荷をぶさらげているので、ダイアゴナルクリッピング歪みなどの影響は無いのか気になります。実際にこの歪に苦しめられたことがありますけど…

クリスタルイヤホンは、図１に示すような圧電素子です。キャパシタ分Ｃが優勢なはずですが、必ず抵抗分ｒがあります。

その理由は単純。イヤホンが鳴るということは、電気エネルギを音や振動の形で放出している事に他なりません。そのため、電気回路上は何らかの形で電気エネルギが消費されています。

この消費は「抵抗」として回路上に現れます。なぜなら電気回路理論において唯一エネルギを消費できる素子だからです。キャパシタやインダクタいった電気回路素子は、一時的にエネルギを蓄えるだけであって、決してエネルギの浪費家ではありません。

逆の立場から見ると、Ｃ分は何も音を出すことに役立っておらず邪魔な存在です。抵抗分が大きければ大きいほど高い効率が期待できるのですから。（もちろん、音にならないエネルギ損失もあるので、その抵抗が絶対に有用だとは限りません・・・）

以上の考察から、絶対値のインピーダンスだけではなく、複素インピーダンスとして計測するのが正しいと思えます。とはいえ、絶対値も十分に有効な指標なので、当然ながら測定はすべきでしょう。

インピーダンスの絶対値を測るのは簡単で、振幅だけを測定できれば良いことになります。もちろん位相までは計測していないので、Ｃ成分ｒ成分の内訳は分かりません。

低周波オシレータに100kΩとイヤホンを直列に接続し、交流電圧計でイヤホンの両端電圧を測定します。

この直列抵抗で計測する手法で図１の回路を測定すると、本質的な系統誤差が出ますが概略を知るには十分でしょう。

誤差率は、ｒが100kΩに比べて十分に小さいと仮定したときε(%)=-100×ｒ/100ｋΩになります）

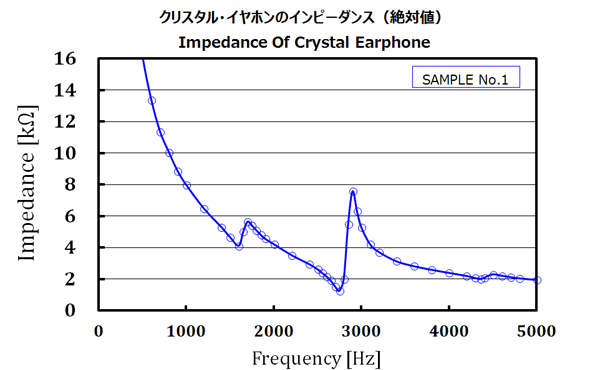
図２．イヤホンのインピーダンス絶対値測定結果

実際に測定してみると予想以上にインピーダンスが低く、周波数による変動が激しいことが分かりました。

1kHzでのインピーダンスはわずか8kΩしかありません。山谷が現れる周波数では、大きくイヤホンが鳴り響き、うるさいぐらいになりました。

明らかにその山谷の周波数で共振していることが分かります。また、その振動周波数に規則性があることも、共振を裏付けています。

もっと正確に「周波数」別の「複素インピーダンス」を測るためにはどうしたらよいかを考えましたが、簡単に精度よく測定できるのは交流ブリッジ回路ではないかと考えました。

すぐに設計して、作りこんだのがこれです。

図３．自作交流ブリッジ

内部はこんな風に作ってあります。

図４．自作交流ブリッジの内部

図５．回路図(クリックで拡大)

設計指針は、（１）ブリッジの平衡を確認するため、イヤホンを使用できること。（２）可変抵抗器は目盛りを直読するのではなく、テスターで読むようにすること、の二点です。

SW1をOFFにすると、各VRが回路から切り離され、テスターで抵抗を測ることができるという工夫。目盛りを振ると較正が大変過ぎですし、個人工作では読み取り誤差が大きくなってしまうので、あきらめました。

信号源側にトランスを入れて平衡度を確保しようと努めましたが、あまり関係ないどろか、トランスの非線形歪が悪さをする始末で、結局OFFにしっぱなしです。

検出はイヤホンだけでなく交流電圧計（ミリバル）を使用できますし、精度も良いのですが、実際に使用してみるとどちらも遜色はありませんでした。平衡が取れると、スーっと波が引いたようにイヤホンが静かになります。 クリスタルイヤホンを使って、クリスタルイヤホンを測定するのは何か不思議な感じです。

実用的に使うためには、様々な周波数で平衡を取らなくてはいけないので、高すぎて聞き取りにくい周波数（5kHz over)や低すぎて聞えない周波数（～10Hz)はミリバルのお世話になりました。

下の図４が測定系です。この中で緩衝増幅器は無くても大丈夫ですが、測定時に信号源側から見たインピーダンスが変化しそうに思えたので念のための措置でした。 （後になって、ブリッジのインピーダンス変化が小さいことを知りましたので、明らかに不要な措置でした。） またＣＲフィルタをミリバルの前に挿入してあるのは、測定ノイズを低減するためであって、無くても大きな影響はありません。

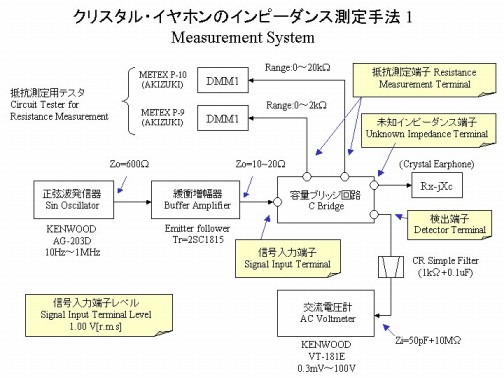
図６．測定系統図

図７が、実際にセラミックタイプのクリスタルイヤホンを測定した結果です。このときイヤホンの口は開いた（開口端）状態で測定してあります。

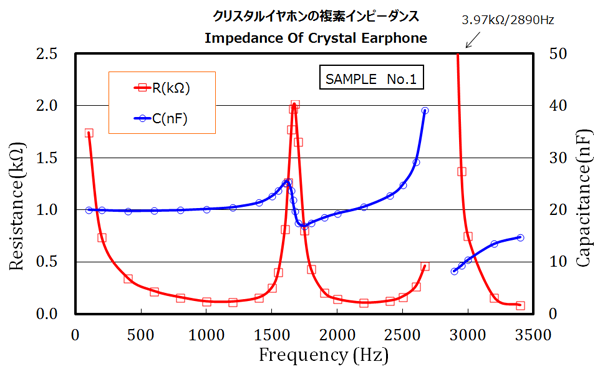
図７．クリスタルイヤホンの複素インピーダンス

複素インピーダンスで測定してみると、ｒとＣの挙動がはっきりしました。1700Hz、2900Hz前後で鋭く共振し、ｒが増大しているのが良く分かります。

注：図５は本来、リアクタンスもΩで表すべきなのですが、周波数範囲が広くわかりずらいため、静電容量に換算してあります）

共振周波数付近では、インピーダンスの絶対値が増大し、イヤホンがよく鳴り響くようになりました。このあたりの周波数では非常に電気音響変換効率がよいということを意味しています。

それ以外の周波数では、おおむね、r=100～400Ω程度の抵抗分しかありません。効率が非常に悪いのです。

電気回路的に見ると、周波数が低いときにはＣ分のリアクタンスが大きくなるわけですが、実測値では抵抗分の変化はあまり無いので、電流がCに妨げられてしまい、効率はどんどん悪化していくことになります。

また、水晶振動子によく似た挙動を虚数分（青線）が表しています。コンデンサの容量が上昇-減少しているように見えるのは、リアクタンスにL成分が発生しているように考えられます。

なお、残念ながら、2800Hz前後（2700Hz-2900Hz）の共振は測定範囲をオーバしてしまい、正確な値は分かりませんでしたが、Ｒ分が極端に大きく、かつ、Ｃ分が極端に減っていますので、この周波数に限っては高効率なイヤホンであるに違いありません。

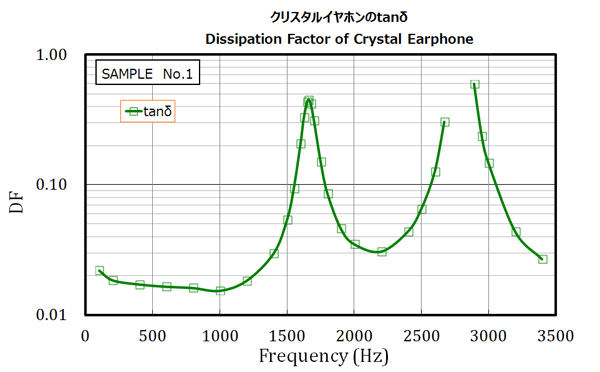
図７－２．クリスタルイヤホンの誘電正接

図7-2は誘電正接(DF)の周波数グラフです。この数字が音響変換効率をほぼ直接的に表すものと考えるのが妥当と思います。 （一部は熱などの音以外のエネルギ損失になるので絶対ではないが、イヤホンが鳴り響くことを考慮すると、おおむね音へ変換されていると思われる。） \[ DF = \tan \delta = \frac{r}{X_c} = \omega C r \] DFは意外に低い周波数でも一定の数値を保ってはいるのですが、100Hz-1500Hz平均で0.03程度とやはり低い水準です。 ピーク値（共振時）には0.4-0.5程度と極端に効率が高くなることが分かります。

ＣＲＬさんが、この測定をさらに進化させて多数のイヤホンの複素インピーダンス測定をされています。当ページで測定不可だった3kHz付近の共振も測定をされています。何とリアクタンスが誘導性になる驚きの事実が！

リンク：ゲルマラジオの試作工房

本物のクリスタルイヤホン（ロッシェル塩型）も測定されていますので、興味のある方はぜひ覗いてみてください。こちらは、ゲルマ用途としても優れた特性です。

クリスタルイヤホン（セラミック型）の電気的特性は、以下のようなものでした。

• インピーダンスが周波数により大幅に変動する
• 300Hzから1.5ｋHzの間の平均で、およそ0.02μF+100～400Ω程度の等価回路に置き換えられる
• いくつかの共振周波数をもつ
• 1kHz付近におけるインピーダンスは8ｋΩ程度
• 共振周波数を除き、効率は極めて低い

よって、ゲルマラジオ用としてのクリスタルイヤホンは「最適な受話器」と言い切れない結果となりました。高感度の電磁型ヘッドフォンや電磁型イヤホン（要するに市販オーディオ用製品）に、トランスを付けて使用した方がもっと高効率・高感度となる可能性を秘めています。

実際、市販の音楽用ヘッドホンに低周波トランスを使って接続した場合には、音質もよく、感度も劣りません。（むしろ音量はヘッドホンの方が大きく感じるぐらい）

ただ、そうは言っても「安価で簡単に鳴るイヤホン」という特質は捨てがたく、有り余るメリットです。生き残っているのも理由があるということでしょう。私も結局はクリスタルイヤホンに頼ってますね。

電気的な特性のクセは、両耳イヤホンによって軽減できそうです。下記の傘ラジオに掲載されている手法です。

それから、クリスタルイヤホンの大容量キャパシタは、受信歪みに影響する恐れが無いのかが非常に疑問であったりします。

大容量のＣを負荷にすると、ダイアゴナルクリッピング歪みが発生するのですが、実感としては極端な歪みを感じる事は稀です。（強烈な歪み経験はありますけど。）

ここが実は謎な部分であって、圧電素子だと多少事情が違うのかもしれません。ざっと計算すると、3kHzまでの信号周波数（変調度0.8）に対して歪まない条件はC=0.02μFの場合、時定数は52μs以下。Rは2.6kΩ以下である必要がでてきます。

また、R=100kΩを使用すると、C=0.02μFから、780Hz以上の信号は歪む勘定です。

しかしながら、実感が湧かないというの何故でしょうか？歪の大半は音質の悪化というよりも音が小さくなるという形での歪が主となっているかもしれませんし、また、単純なＣと考えることが誤っているのかもしれません。

今後は、音質改善方法やtanδの増やし方を探っていくことにしましょう。どうやら音響条件（イヤホンを耳に挿入するか、開口状態にするかなど）で電気的特性が変化します。つまり、内部の機械的な改造によって、よりよい状態にできる可能性があると見ています。

測れば測るほど、不明な点が増えていく…セラミックイヤホンはそんなデバイスなのでした。

容量交流ブリッジの理論は、基本的な電気回路理論によって導かれます。

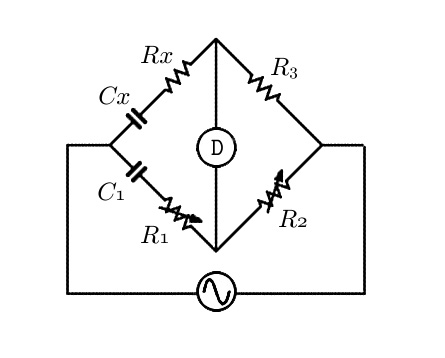
図８.容量ブリッジ回路

図８が基本回路図（容量ブリッジ）です。R1とR2を可変し、検出器Ｄに信号が現れなくなったときに回路の平衡が取れ、未知容量Cxと未知抵抗Rxを求めることができます。

平衡操作は根気が必要ですので、あしからず。平衡が取れたときのCxとRxはそれぞれ \[ C_x = \frac{R_2}{R_3} C_1 \tag{1} \] \[ R_x = \frac{R_1}{R_2} R_3 \tag{2} \] と計算によって求めることができます。なお、検出器Ｄには何を用いてもよく、イヤホンや交流電圧計が用いられます。

導出は比較的簡単で、まず、交流ブリッジ回路の平衡基本式 \[ \dot{Z_1} \cdot \dot{Z_3} = \dot{Z_2} \cdot \dot{Z_4} \tag{3} \] を、回路にそのまま当てはめると、 \[ R_3 \left( R_1 + \frac{1}{j\omega C_1} \right) = R_2 \left( R_x + \frac{1}{j\omega C_x} \right) \tag{4} \] となり、これを実数項、虚数項にまとめなおすと \[ (R_1 R_3 - R_2 R_x) + j \left( \frac{R_3}{\omega C_1} - \frac{R_2}{\omega C_x} \right) = 0 \tag{5} \] となります。

式(4)が成立するためには、実数項、虚数項の両方が0となる必要があります。すなわち \[ R_1 R_3 = R_2 R_x \tag{6} \] 及び \[ \frac{R_3}{\omega C_1} = \frac{R_2}{\omega C_x} \tag{7} \] が平衡条件となり、最終的に、 \[ C_x = \frac{R_2}{R_3} C_1 \tag{1} \] \[ R_x = \frac{R_1}{R_2} R_3 \tag{2} \] が得られます。