包絡線検波器（ダイオード検波器）の理論解析１

はじめに

本ページでは、一般に包絡線検波器あるいはダイオード検波器と呼ばれる回路動作の理論的な解析を紹介するページです。

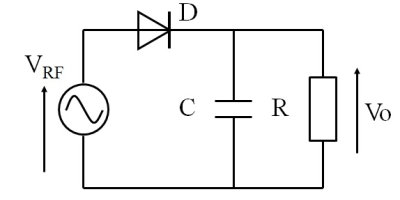
図１.ダイオード検波器（包絡線検波器）

この古典的な検波器は、ゲルマラジオ・鉱石ラジオの心臓部であり、その単純さから小学生の教材になるほど簡単な回路です。

しかし、その詳細な動作を「正確に解析し理解する」のは、なかなか難しい回路でもあります。単純な近似理論であってさえも、手計算で入出力を求めることはかなりの労苦を伴います。

市販の電子回路教科書には必ず載っているほど有名な回路なのに、計算の詳細が載るのは稀であるのも、そういう事情があっての事でしょう。載っていても、７０年以上前に真空管（２極管）を意図して解析された内容であるので、少し物足りない面もあります。

そこで、検波器の基本的な入出力特性を求めて行こうというのが本ページの趣旨です。

要約

入力ＲＦ(Radio Frequency)信号、 $ v_{RF} = V_c \cos(\omega t) $ を入力したとき、キャパシタＣが十分にＲＦ電流を短絡していると仮定すれば、出力直流電圧Voは、以下の式(1)を満足する値として定まる。

\begin{eqnarray} V_T \ln \left[f_0 \left( \frac{V_c}{V_T} \right)\right] -V_T \ln \left[ 1 + \frac{V_o}{I_s R_o} \right] - V_o = 0 \tag{1} \end{eqnarray}

ここで、各変数は

$V_c$: 入力ＲＦ振幅電圧[V]
$V_o$: 出力直流電圧[V] (V out)
$V_T$: ダイオードの熱電圧[V]
$I_s$: ダイオードの逆方向飽和電流[A]
$R_o$: 負荷抵抗[Ω]
$\ln(x)$: 自然対数 ($\log_e x$)
$f_0(x)$: 第１種０次変形ベッセル関数

第１種０次変形ベッセル関数 $f_0(x)$ は特殊関数の一種です。数学ではこれを $I_0(x)$ と書くことが多いのですが、電流 $I$ の表示と紛らわしいため、ここでは違う表記にしてあります。この関数の積分表示や無限級数表示式は以下の通りです。$ J_0(x) $は第１種０次ベッセル関数、$ j $は虚数単位。）

\begin{eqnarray} f_0(x) &=& J_0(jx) \\ &=& \frac{1}{\pi} \int_{0}^{\pi} e^{x \cos \theta} d \theta \\ &=& \sum_{k=0}^{\infty} \frac{(x^2/4)^{k}}{(k!)^2} \tag{2} \end{eqnarray}

式(1)は、簡単な手計算では求められない非線形の式であるため、Newton法などの数値シミュレーション技法で何とかします。

要するに、とんでもなく面倒で複雑です。

手計算は大変
ダイオード特性を知る必要あり
変数が多い

（付録３）理論式の導出過程

大まかな特性の把握

最初から数式だけだとアレなので、大雑把に検波器の入出力特性を考えていきます。

まず、式(1)の複雑な数式を言葉で書き直してみると、

\[ 直流起電力 - ダイオードの電圧降下 = 出力電圧 \]

という簡単な式であったりします。

直流起電力（無負荷出力電圧）

ダイオードに高周波電流が流れると、その非線形特性によってさまざまな周波数の起電力が発生します。その一つが直流成分です。

重要なことは、ダイオードの種類とほぼ無関係に、直流起電力が定まることです。そのほとんどはＲＦ入力電圧のみで決まると見てよいでしょう。

\[ V_T \ln \left[f_0 \left(\frac{V_c}{V_T} \right) \right] \tag{3} \]

この式には、入力ＲＦ電圧の $V_c$ と、熱電圧 $V_T$ の２つの変数しかありません。

熱電圧は室温（２７度＝３００Ｋ）で約２６ｍＶ程度となり、現実のダイオードであっても、２５ｍＶから３５ｍＶ程度の間におさまる値ですから、ほとんど入力電圧振幅 $V_c$だけで起電力が決まってしまうのです。

この起電力の値は、入力ＲＦ振幅が小さくなると急激に減少する特性があり、検波効率が極端に悪化します。無負荷の状態、すなわち最大の出力電圧が得られるときの検波効率=Vo/Vcを計算したのが図２です。

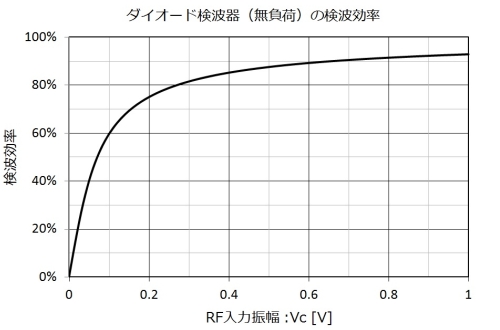
図２．無負荷時の検波効率

ある程度のＲＦ入力があれば、100%に近い検波効率が得られますが、小信号だと急激に悪化するのがよくわかると思います。

本来は、小信号ほど検波効率を上げて感度を高めたいのですが、ゲルマ／鉱石ラジオが本来持っている特性は、小信号ほど余計に感度が悪化するという結論です。

すなわち、高感度を目指すには、ＲＦ電流ではなくＲＦ電圧を重視しなければならず、同じＲＦパワーならば、同調回路を使って最大限に昇圧を掛ける必要があるのです。

ダイオードの電圧降下

ダイオードや鉱石の種類によって感度が違うという最大の原因がこれです。

起電力は変わらずとも、ダイオードを取り替えると感度が良くなったり悪くなったりするのは、この電圧降下の大小が違うからです。

この電圧降下は、ダイオードに流れる直流電流 $I_{dc} = V_o/R_o $ によるものです。

\[ V_T \ln \left( 1 + \frac{V_o}{I_s \cdot R} \right) = V_T \ln \left( 1 + \frac{I_{dc}}{I_s} \right) \tag{4} \]

個々のダイオードは、式(4)中の Is→逆方向飽和電流が非常に広範囲にバラつきます。何％というレベルではなく、１０桁ぐらいに。

シリコンダイオードで、fAからnA（フェムト～ナノアンペア）程度。ゲルマニウムダイオード、鉱石、あるいはショットーバリアダイオードにおいては、nAからμA（ナノ～マイクロアンペア）程度となります。

Isが大きいダイオードほど、電圧降下が小さく高感度になります。

１Ｖ以上の強い信号入力があれば、その差も無視できるのですが、微弱信号を相手に戦う鉱石ラジオでは、感度に大きな差が出てしまいます。

なお、この値は温度の影響を非常に受けやすいことが知られており、ダイオードを熱するとIsも上昇します。ダイオードを炎で炙り、高感度にした事例も存在します。（正確には絶対温度の３乗に比例してIsも増加する。）

直流の等価回路

以上の２つの式を回路図で表現したのが、図２です。

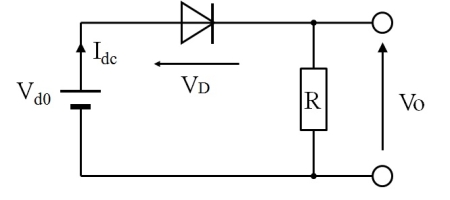
図２．ダイオード検波器の直流等価回路

非常にシンプルな等価回路です。しかし、このダイオード・抵抗直列回路は、その単純さとは裏腹に、複雑な計算の繰り返しを要求される手ごわい回路！

この単純で厄介な非線形回路のせいで、簡単に答えが求まらず、シミュレーションに頼ることとなります。まぁSPICEを用意しなくても、ExcelやLibre office Calcがあれば、何セルかの計算で求められますけど・・・

無負荷時の検波特性（起電力）の詳細

検波器から最大の出力電圧が得られるのは、図３のような無負荷のとき、すなわち抵抗器Ｒを接続しないときです。

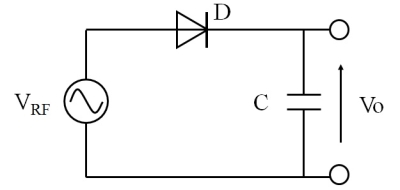
図３．無負荷状態のダイオード検波器

この電圧は、ダイオードから発生する直流起電力そのものであって、負荷抵抗があってもなくてもこの起電力自体には変化がありません。

もっとも、この回路は原理的にＡＭの復調性能が無く、実用的にもあまり振幅が変化しない静的な信号検出にしか使えないため、ゲルマ／鉱石ラジオ用には不向きです。特に高性能なダイオードを使用すると、ダイアゴナルクリッピング歪やネガティブピーククリッピング歪が発生し、聞くに耐えない音質になる場合もあります。

ダイオード熱電圧の影響度

無負荷状態の本回路の出力電圧は、入力ＲＦ電圧 $V_c$ と熱電圧 $V_T$ のみによって決まり、以下のような式となります。

\[ V_o = V_T \ln \left[f_0 \left(\frac{V_c}{V_T} \right) \right] \tag{5} \]

では、この回路の入出力特性が、ダイオードの熱電圧V_Tにどの程度の影響を与えるか調べるため、25、30、35mVの３つの値をグラフに描いたものが図４です。

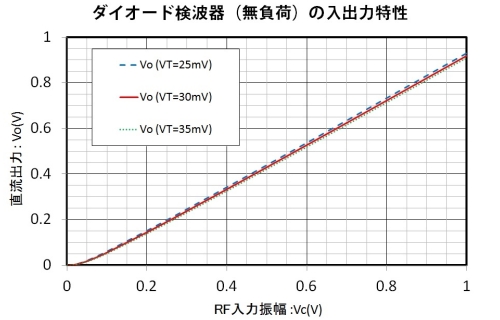
図４．無負荷検波器の入出力特性

これを見ると、熱電圧V_Tの違いは無視できそうです。もっとも、$V_T$が小さいほど、出力電圧が大きくなるのも確かといえば確かです。以後は、熱電圧$V_T$を26mV一定として解析していきます。

小信号入力時の近似

無負荷検波においてＲＦ信号が小さいときは２乗特性が現れます。特に26mVを下回ると明確な２乗特性となり、34mVの入力までなら誤差10%以内で計算することができます。（２乗特性近似）

\[ V_o \simeq \frac{V_c^2}{4V_T} \ ,(V_c \leq V_T) \tag{6-1} \]

より正確に小信号の出力を計算したいのであれば、以下の補正式を使用すれば52mV以下の入力で誤差を1.3%以内に抑えられます。本式は、理論的な補正式を導出した後に、さらに私自身が数値シミュレーションにて微調整したものです。（２乗特性補正近似）

\[ V_o \approx \frac{V_c^2}{4V_T} \left(1 - \frac{V_c^2}{21.5 V_T^2} \right) \ , (V_c \leq 2V_T) ,\ |\epsilon| \leq 1.3\% \tag{6-2} \]

図５は、小信号領域での特性図です。

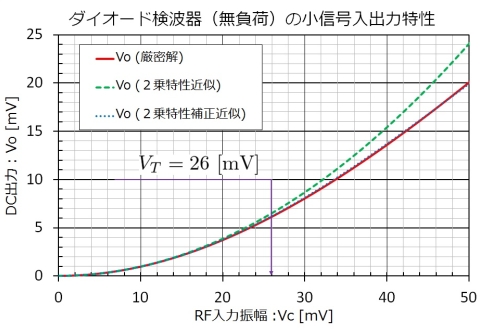
図５．小信号入力時の無負荷検波器特性

大信号入力時の近似

無負荷検波器に大信号を入力した時には直線検波特性が現れます。具体的には、300mV以上の入力であれば、ほぼ入力に直接比例した出力が得られます。また、1V以上あれば完全に直線と見なしてよいでしょう。

入力ＲＦ信号が十分大きいとき、具体的には52mVを超える場合には、次式で出力を表すことができます。（漸近展開１次近似）

\[ V_o \simeq V_c -0.92 V_T - \frac{V_T}{2} \ln \left( \frac{V_c}{V_T}\right) \tag{7} \]

上の式は、入力が大きいと仮定して解いた近似式のため、小入力のときには誤差が大きく、52mVの入力では-11%の誤差があります。130mV以上で誤差1%以下におさまります。

もし、より計算精度が欲しい場合には次式を使うことで近似度が上がります。52mV入力で-3.4%、74mV以上で-1%以下です。（漸近展開２次近似）

\[ V_o \simeq V_c -0.92 V_T - \frac{V_T}{2} \ln \left( \frac{V_c}{V_T}\right) + \frac{V_T^2}{8 V_c} \\ , (V_c \geq 2 V_T) , \ |\epsilon| ＜ 3.4 \% \tag{8} \]

いずれの式を用いても、300mV以上の入力があれば誤差は0.2%を十分に下回るので、一般測定器以上の精度で計算ができると思います。

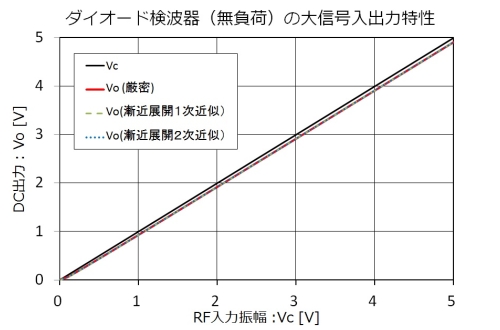
図６．大信号入力時の無負荷検波器特性

図６の最も上の直線が入力電圧振幅です。これを見ると、入力のVcが、ほとんどそのままVoとなり、検波効率が100%に近づいていることが見て取れます。

(参考)Excel/Calcでの起電力計算

Microsoft ExcelやLibre Office Calcでは、組み込み関数として、変形ベッセル関数まで用意されているので、１セルでダイオード起電力を計算することができます。

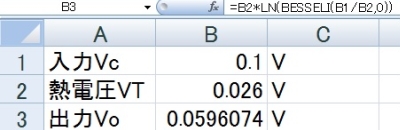
図８．Excelを使ったダイオード起電力計算

計算式は、=0.026*LN(BESSELI(入力電圧/0.026,0))の１行で計算できます。ExcelやCalcにおいては、変形ベッセル関数とは言わず、なぜか「修正ベッセル関数」と呼んでいて、0次の計算をするためには、=BESSELI(x,0)とします(xは変数)。Excel2003まではエンジニアリング関数の組み込みが必要ですが、Excel2007以降はデフォルトでも関数が使用できます。

なお、Libre Office Calcでの計算方法も全く同じです。それと少なくともExcelでは6桁程度の精度のようです。

（続き）包絡線検波器の理論解析２へ