09.DC分布定数回路の減衰定数とミステリー

損失の単位

前ページで得られたDC分布定数回路における電圧・電流の位置関数（分布関数）には、 \(V_1,V_2,I_1,I_2 \) ４つの積分定数があり、初見では具体性が見えにくいところです。

\begin{eqnarray} V(x) &=& V_1 e^{-\sqrt{RG}x} + V_2 e^{\sqrt{RG}x} \tag{8.3} \\ I(x) &=& I_1 e^{-\sqrt{RG}x} + I_2 e^{\sqrt{RG}x} \tag{8.6} \end{eqnarray}
ここから式の簡素化のために、大量に現れる \(\sqrt{RG}\) の項を １変数で表すことにします。 \[ \alpha = \sqrt{RG} \tag{9.1} \] この \( \alpha\) は物理的に距離の逆数の単位をもちます。SI単位系であれば \[ \alpha \equiv \sqrt{ \left( \frac{\mathrm{Ohm}}{\mathrm{meter}} \right) \left( \frac{\mathrm{Siemens}}{\mathrm{meter}} \right)} = \frac{1}{\mathrm{meter}} = \mathrm{m^{-1}} \] と表現できる量です。これでもう少し式が見やすくなりますね。
\begin{eqnarray} V(x) &=& V_1 e^{-\alpha x} + V_2 e^{\alpha x} \tag{9.3} \\ I(x) &=& I_1 e^{-\alpha x} + I_2 e^{\alpha x} \tag{9.4} \end{eqnarray}

ここで見えてくる \(\alpha x\) の項は、距離 \( x \)と の掛け算した結果「無単位」の量になっています。要は距離に応じた電圧・電流の比率を表しているわけです。

その比率 \( \alpha \) を減衰定数といいます。

\(\alpha \) という量は単位長あたりの入出力電圧比を「自然対数」で表現したものであって、 \( \alpha = 1 \) であれば、 1mあたり 36.8% (1/e) に減衰する度合いです(SI単位系)。

これを 1 [Np/m] （ネーパ毎メートル: Nepers per Meter）と呼ぶことになってますが使ってる人見たことありません。常用対数に変換した 8.686 [dB/m] とする方が工学系単位としてより馴染みのある表現になるでしょう。

\[ \alpha = (20 \log_{10} e ) \ \sqrt{RG} = 8.686 \times \sqrt{RG} \ \ \mathrm{[dB/m]} \]

つまり、 R = 1 [Ω/m] , G = 1 [S/m] の分布定数をもつ線路の場合、 1m 遠くなるごとに電圧と電流が36.8% の割合で減少し続けることになります。

電線の損失を抑えるためには抵抗を小さくすること(R->0)、漏洩を少なくすること(G->0)が鉄則なわけですが、直感的に合致していることも理解できると思います。

しかしながら、式(9.3),(9.4)には、「減衰しない項」が含まれています、これはどういった理由でしょうか？

第2項「電圧電流上昇」をめぐる解釈

指数関数 \( y = e^{-x} \) のグラフを描くと、 \(x\) がプラス方向（右方向）に大きくなるにつれて、\(y\) は減少していきます。

これは \( V_1 e^{-\alpha x}\) という項に対応していて、単純に遠くなるほど電圧・電流が減少していくことを示しているだけです。

では、 \(x=0\) の場所に起電力 \(E_1\) の電池をつないだときの電圧はどうなるでしょうか。fig(9.1) は長さ \(l\) の線路に電池を接続して、終端を開放した状態です。

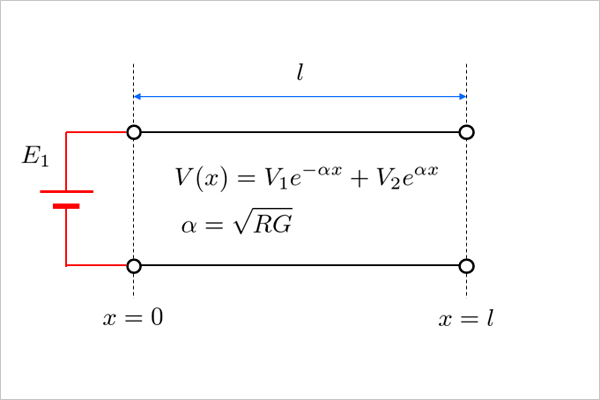
Open Transmission Line

fig9.1 片端開放状態の直流伝送路

距離0m（始端）では電池電圧 \(E_1 \) に電位が固定されますが、電圧の積分定数 \(V_1\) とは等しくなりません。第2項である \(V_2\) の影響が出てくるからです。

fig(9.1)の条件では、始点で \(e^0=1\) のため、 \[ E_1 = V(0) = V_1 + V_2 \] が成り立っていて、どうやら \(V_2\) も含めて計算するらしいことが見えてきます。

ところで、 \(V_2 e^{\alpha x}\) 項は、電池から距離が遠くなるほど電圧が上昇する項です。次のグラフは \(y=e^x\) を描いたものですが、遠距離になるほど昇圧していく様子がわかります。

抵抗のみで構成された線路なのに、電位がどんどん上がっていくのは物理的に無理がありそうですが、これにはちゃんとした理由が存在します。

このこのミステリアスな項、実は終端側から始端側への影響なのです。

つまり、線路を左右ひっくり返して終端をスタート地点として据えたとき、電圧・電流が「減衰しながら」始端に向かっていく様子を捉えているだけなのでした。

これで一安心…と思っては危うし。このとき終端には何もつながらない 'OPEN' の状態、電池も何もつながっていないのだから \(V_2=0\) なのだろうと早とちりしてはいけません。 この条件で計算した結果を先に書くならば、

\begin{eqnarray} V_2 &=& \frac{E_1}{1+e^{2 \alpha l}} \\ V_1 &=& \frac{E_1}{1+e^{-2 \alpha l}} \end{eqnarray}
と、いう結果が得られてしまうのです。これも終端の影響です。では直流伝送路全体で何が起きているのでしょうか。

次ページからは、この辺の詳細計算を進めていきます。