07.直流の分布定数回路を考える

直流における分布定数回路の考え方

前ページでは、Ｔ型抵抗回路を多段分割しまくると、全体の合計値で評価した方がよさそうなことが見えてきました。

しかしながら、無限に分割するのはあまり物理的な意味は薄そうです。なにせ1段あたりの抵抗値が発散・消滅し、その積分量(\(\theta_k,Z_k,R_t,G_t\))は残るものの、任意の段の電位までは考えられなくなってしまうからです。（入力と出力しかないカタマリとしてなら評価可能。）

そこで、ここからは「距離（サイズ）」という概念を導入することで、「1段」という自然数に基いた考え方から脱却しましょう。

これまで考えてきたT形回路には距離という概念がありません。でも実在の抵抗体は必ず大きさがあり、３次元の空間を占有しています。電気回路理論の利点はサイズに関係する諸量を抵抗値という代表選手に全て押し付けて単純化できることに尽きるでしょう。とは言うものの、縦・横・高さの3次元まで考えるとやはり面倒なので、せめて「長さ」という1次元だけで考えたいものです

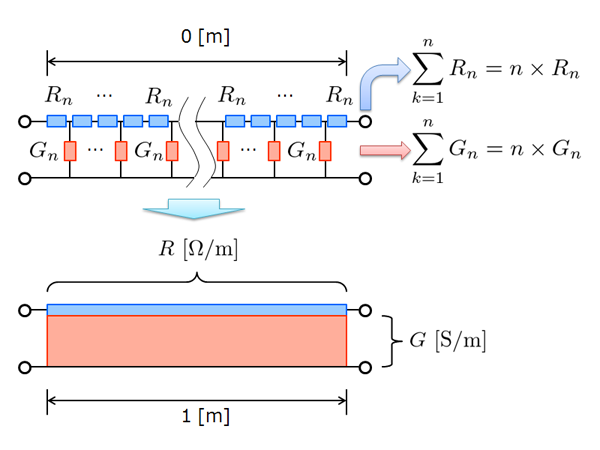
fig7.1 集中定数回路から分布定数回路へ

上の fig.7.1 は、この考え方をまとめたものです。まんべんなく直列抵抗 \(R\) と漏れコンダクタンス \(G\) が分布していると仮定します。これまでの「段」との違いは、長さというモノサシが導入されていることです。

長さというのは1段,2段,3段といった自然数ではなく、例えば \(\sqrt{2} \) といった実数で表現ができる単位です。ここが嬉しいところ

とは言うものの、 R という記号の意味が変わります。これまで[Ω]という単位であった R は、ここからは「1mあたりの抵抗値」である[Ω/m]になるのです。

具体的な例を考えてみると、抵抗率の高い材料で製造された同軸ケーブルを考えるとよさそうです。例えばカーボン（炭素）で中心導体をつくり、外部導体との間にシリコンやニクロムのような高抵抗の物質を充填すればこのモデルで表現できそうです。また、簡単化したいので外部導体は 0Ω としてしまいます。（有限の抵抗値でも実際は問題ない。）

fig.7.2 にイメージ図を示します。

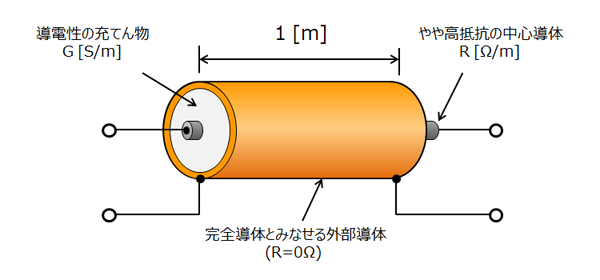
fig7.2 具体的なイメージ

このモデルで重要なことは、内外導体間の G による漏れ電流が断面に対して垂直に流れると仮定できることです。構造が均質でなく電流分布が複雑な場合は適用条件を吟味する必要性があります。

直流分布定数モデル

fig.7.2 のイメージを回路図で書き直したものが、下の fig.7.3 です。

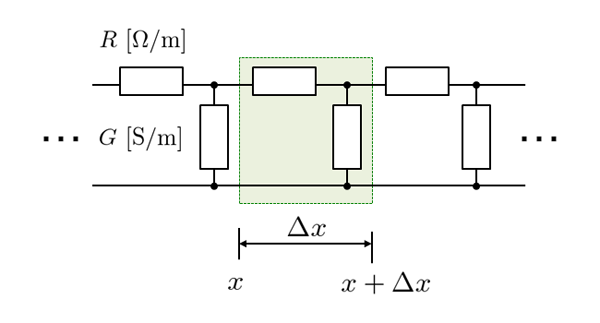
fig7.3 分布定数のモデル

きわめて微小な長さ区間 \(\Delta x\) を切り出しても、R=0[Ω] や G=0[S] になりません。どんなに小さく切り出してもよいです。

以下の fig7.4 で微小距離 \(\Delta x\) での回路方程式を完成させます。

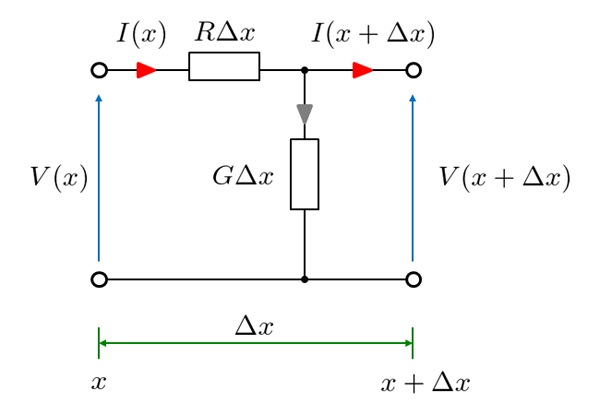
fig7.4 分布定数のモデル

直列抵抗 R はあくまで 1m あたりの抵抗分布量なので、オームの法則を適用するには距離をかける必要があります。漏れコンダクタンス G も同様。結果として、それぞれ \(R \Delta x \ \mathrm{[\Omega]}\) , \(G \Delta x \ \mathrm{[S]}\) としなくてはなりません。

図の左側が入力電圧・電流（距離 \(x\)）として, 右側が \(\Delta x\) の距離を経た後の出力電圧・電流（距離 \(x+\Delta x\)）としています。

入力電圧 \(V(x)\) が、 R で電圧降下すると \(V(x+\Delta x)\) になり、入力電流 \(I(x)\) が、 G で電流漏洩すると \(I(x+\Delta x)\) になります。これらを式にまとめると、以下のようになります。

\begin{eqnarray} V(x+\Delta x) &=& V(x)-R \cdot \Delta x \cdot I(x) \tag{7.1} \\ I(x+\Delta x) &=& I(x)-G \cdot \Delta x \cdot V(x+\Delta x) \tag{7.2} \end{eqnarray}

電圧の微分方程式をつくる

式7.1 を工夫して極限をとれば、微分方程式の出来上がりです。

\[ V(x+\Delta x) = V(x)-R \cdot \Delta x \cdot I(x) \tag{7.1} \]

から、

\[ \frac{V(x+\Delta x) -V(x)}{\Delta x} = - R I(x) \tag{7.3} \]

あとは、\(\Delta x\)の極限を取り

\[ \lim_{\Delta x \to 0} \frac{V(x+\Delta x) -V(x)}{\Delta x} = \frac{dV(x)}{dx} \]

要は、微分の定義そのものになるんです。結果として、電圧に関する微分方程式は

\[ \frac{dV(x)}{dx}=-R I(x) \tag{7.3} \]

もう、ここまでくると \(V(x),I(x)\) の表記が煩わしいので、 \(V(x)=V ,I(x)=I\) と省略するとして、

\[ \frac{dV}{dx}=-R I \tag{7.4} \]

これで完成です。

電流の微分方程式をつくる

式7.2も電圧式と同様な操作で、微分方程式が作れます。

\[ I(x+\Delta x) = I(x)-G \cdot \Delta x \cdot V(x+\Delta x) \tag{7.2} \]

から変形し、

\[ \frac{I(x+\Delta x) -I(x)}{\Delta x}= -G \cdot V(x + \Delta x) \tag{7.5} \]

として、 \(\Delta x\) の極限を取り

\[ \lim_{\Delta x \to 0} \frac{I(x+\Delta x) -I(x)}{\Delta x} = \frac{dI}{dx} \tag{7.6} \]

一方、右辺の方は、単純に

\[ \lim_{\Delta x \to 0} -G \cdot V(x + \Delta x) = -GV(x) \tag{7.7} \]

となるので、最終的に

\[ \frac{dI}{dx} = -GV \tag{7.8} \]

という方程式にたどりつきます。

微分方程式のまとめ

直流分布定数回路の微分方程式は、以下の２式にまとまりました。

\begin{eqnarray} \frac{dV}{dx} &=&-R I \tag{7.4} \\ \frac{dI}{dx} &=& -GV \tag{7.8} \end{eqnarray}

ここで \(V,I\) は \(V=V(x) , I=I(x)\) という距離の関数であることに注意してください。マイナスが付いているのは、距離が伸びるほど電圧・電流が減少することを意味します。

電圧降下の割合は、分布抵抗 R と電流に反比例すること。電流減少の割合は、分布コンダクタンス G と電圧に反比例することを表しています。

この２式は相互に影響しあっていますので、ケーブル上の電圧・電流分布を求めるには、もう一工夫必要です。次ページでは、そのあたりの作業をやっていこうと思います。

次ページへ続く