前ページでは、T型抵抗回路を同一特性を保ったまま多段分割していくとどうなるかという計算をしてみました。当然のごとく、それを無限段に至るまで分割数を増やしていくのも自然な流れでしょう。
すると、あまり嬉しくない事態が待っています。「T型回路段数のn」を十分に増やしたとき…具体的には1千程度から、百万程度にとりあえず分割してみると分かるのですが、段数が増えるに従って1つの単位段あたりの特性の意味が薄れてきます。
先ほどと同じ、元の1段が R=1[Ω] と r=4[Ω]の抵抗で構成されたT型回路を例にとります。仮に100万分割すると、各段の抵抗はそれぞれ
\begin{eqnarray}
R &=& \frac{3 \ln 2}{2 \times 10^6} = 1.0397 \mathrm{[\mu \Omega]} \\
r &=& \frac{3 \times 10^6}{\ln2} = 4.3281 \mathrm{[M \Omega]}
\end{eqnarray}
となる計算です。
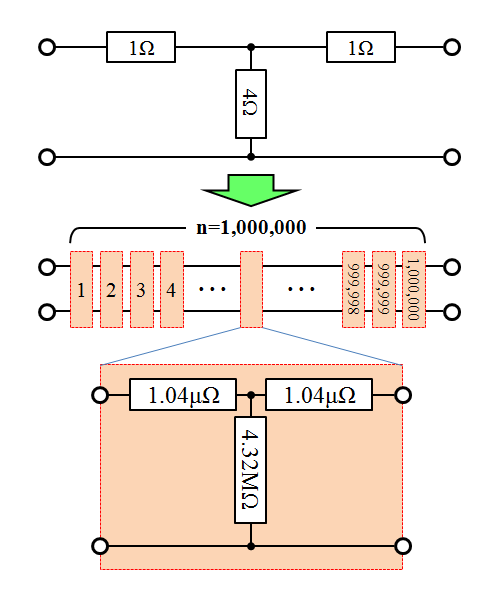
fig6.1 T型回路を100万分割した場合の例
直列抵抗値Rは非常に小さくなり、並列抵抗値rは極端に大きくなるのは当然のこと。ただ、一応は各段の諸量を計算することは可能なのですが、これを無限に分割していくことを考えると
\begin{eqnarray}
R_{\infty} &=& 0 \mathrm{[\Omega]} \\
r_{\infty} &=& \infty \mathrm{[\Omega]}
\end{eqnarray}
に収束して行くことになります。これでは、各1段あたりの物理量という意味合いが完全に消えてしまうことに。
すなわち、T型回路は「有限の自然数n」で定義できる範囲での分割しか、あまり意味がなさそうということです。無限段のT型回路縦続接続(抵抗ラダー)は考える事ができても、
有限の特性をもったT型回路を無限分割するというのは少し考える必要がありそうです。
では、有限ではあるが段数nが極めて大きい場合を考えてみます。とにかく1億分割だろうが1兆分割だろうが、∞でなければ有限は有限。
このとき、1段あたりの \(R\) や \(r=1/G\) は計算可能な有限値ではあるのですが、あまり重要とは思えなくなります。このようなときの評価量としては、縦続回路全体の \(R\) や \(r\) の合計値という測度が役立ってきます。
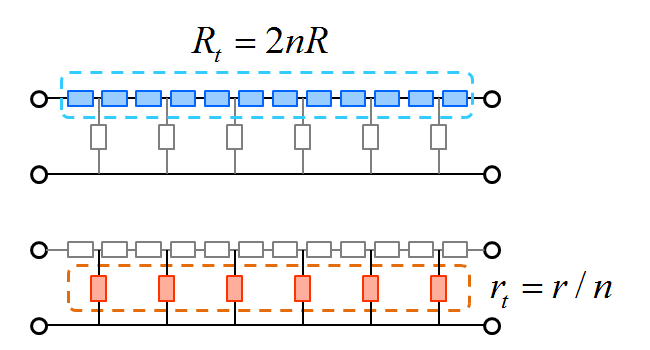
fig6.2 縦続T型回路における合成抵抗値の考え方
先ほどの例と同様に、1段が R=1[Ω] と r=4[Ω]のT型回路を分割していった場合のことを考え、全体の直列抵抗合計値を \(R_t = 2 n R\) 、全体の並列抵抗合成値を \(r_t = r/n\) とおくと、
\begin{eqnarray}
R_t &=& 2nR = 2n \frac{3 \ln 2}{2n} = 2.0794 \mathrm{[\Omega]} \\
r_t &=& \frac{r}{n} = \frac{3n}{n \ln 2} = 4.3281 \mathrm{[\Omega]}
\end{eqnarray}
となって、意味の分かりやすい数値に落ち着くことになります。しかも、
これは十分に大きな分割段数nを仮定さえすれば、分割数に関係ない値です。
無限を「目指して」回路を分割していくとき、各段ごとの抵抗値の意味が薄れていく代わりに、全体の合計抵抗値は分割数にほぼ依存せず一定値を保つわけです。事実、無限分割してもこのことは成立します。(→下段参考へ)
とはいえ、無限分割状態を考えてみてもスッキリしません。この原因は独立した回路が整数個並ぶという電気回路構成にあり、連続した実数を相手とする微積分の考え方とはソリが合わないことにあるのでしょう。
ここまでが集中定数回路の限界です。次ページからは、微積分が可能で物理的にも自然な滑らかな回路構成(分布定数回路)を考えていきます。
次ページへ続く
物理的な意味がどこまであるかは別として、参考として無限分割したときの諸量を計算してみます。
ある特性をもった1段のT型回路をn段に分割するとして、その回路が伝送量 \(\theta_k\) , 反復インピーダンス \(Z_k\) であるとします。 n段に分割したときの直列抵抗 \(R_n\) ,並列コンダクタンス \(G_n\) との関係は以下のようになります。
\begin{eqnarray}
R_n &=& Z_k \tanh \left(\frac{\theta_k}{2n}\right) \\
G_n &=& \frac{1}{Z_k} \sinh \left(\frac{\theta_k}{n}\right)
\end{eqnarray}
ここで、 \(R_n,G_n\) の全体合計値をそれぞれ \(R_t,G_t\) とすれば、
\begin{eqnarray}
R_t &=& 2 n R_n = 2 n Z_k \tanh \left(\frac{\theta_k}{2n}\right) \\
G_t &=& n G_n = \frac{n}{Z_k} \sinh \left(\frac{\theta_k}{n}\right)
\end{eqnarray}
となり、これらは一定値に収束すると仮定しておきます。さらに、この2量の積をとると、
\begin{eqnarray}
R_t G_t &=& 2 n^2 \tanh \left(\frac{\theta_k}{2n}\right) \sinh \left(\frac{\theta_k}{n}\right) \\
&=& 2 n^2 \left\{ \cosh \left(\frac{\theta_k}{n}\right) -1 \right\}
\end{eqnarray}
が得られるので、 \(n \to \infty\) の極限を取っていきます。 計算は \(\infty \times 0 \) タイプとなるので極限値はありそうです。cosh関数を展開して \(2n^2\) をかける形にすれば、
\begin{eqnarray}
\lim_{n \to \infty} R_t G_t
&=& \lim_{n \to \infty}
2 n^2 \
\left\{
1 + \frac{1}{2!} \left( \frac{\theta_k}{n} \right)^2
+ \frac{1}{4!} \left( \frac{\theta_k}{n} \right)^4
+ \cdots -1
\right\} \\
&=& \lim_{n \to \infty}
\left\{
\theta_k^2
+ \frac{2}{4!} \cdot \frac{\theta_k^4}{n^2}
+ \frac{2}{6!} \cdot \frac{\theta_k^6}{n^4}
+ \cdots
\right\} \\
&=& \theta_k^2
\end{eqnarray}
つまり、無限分割できると仮定したときには、
\[
\theta_k = \sqrt{R_t G_t}
\]
が成立します。
続いてもう一つの量 , \(R_t / G_t\) を計算してみます。
\begin{eqnarray}
\frac{R_t}{G_t} &=& \cfrac
{2 n Z_k \tanh (\theta_k/2n)}
{\cfrac{n}{Z_k} \sinh (\theta_k/n)} \\
&=& 2 Z_k^2 \left( \frac {\tanh (\theta_k/2n)}{\sinh (\theta_k/n)}\right) \\
&=& Z_k^2 \left( \frac {2}{\cosh (\theta_k/n) +1 }\right)
\end{eqnarray}
と、少しだけシンプルな式となりました。この極限 \(n \to \infty\) は簡単に求められて、 cosh(0)=1 となることから
\[
\lim_{n \to \infty} \frac{R_t}{G_t} = Z_k^2
\]
に収束します。よって、
\[
\lim_{n \to \infty} \sqrt{\frac{R_t}{G_t}} = Z_k
\]
無限分割すると、T型回路という計算単位は無意味となって、その積分量(伝送量、反復インピーダンス、直列抵抗と並列コンダクタンスの積分値)だけが残ることになります。
なお、最初に収束仮定しておいた \(R_t,G_t\)自体も級数展開しておけば収束するのがよく分かるのですが、
\begin{eqnarray}
\lim_{n \to \infty} R_t &=& Z_k \theta_k \\
\lim_{n \to \infty} G_t &=& \theta_k / Z_k
\end{eqnarray}
になることから、4つの量があるものの自由度は2であり、いずれか2つの状態が既知であれば全ての量を計算することが可能です。
この結果自体は後述する分布定数回路の数値と一致する(物理単位を除く)のですが、第m段目といった任意の段数での電圧値が答えられず、入出力端子だけのブラックボックスとして扱う必要があるでしょう。
また、サイズというディメンションを持たない、つまり「大きさ」ゼロのT型抵抗ネットワークが無限個集まっている意味は何なのか、今一つ理解できそうにないのが難点です。
次ページへ続く

