05.T型回路の無限分割(1)
T型回路を同一特性で分割する
前ページで、無限ラダー回路の要素(T型回路)の諸特性を計算してみました
Fパラメータによる計算の利点は、同じ回路を繋ぎ合わせるときの計算が簡単であることに尽きます。そこで、同一特性を保ったまま回路を2個に分割するとどうなるのか考えてみましょう。
無限に細かく分割していく分布定数回路の最初の一歩です。
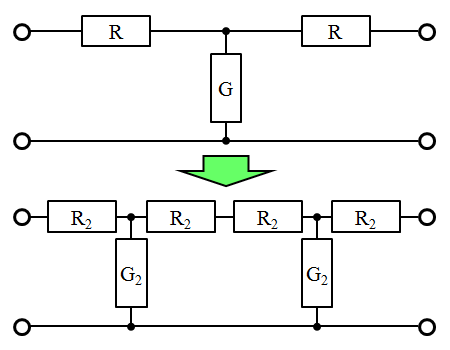
fig5.1 T型回路の分割
まず、T型回路の抵抗RとコンダクタンスGは、伝送量 \(\theta_k\) 及び 反復インピーダンス \(Z_k\) を用いて、
このとき、2つの回路の伝送量 \(\theta_k\) は、2つの回路それぞれの伝送量の和となります。
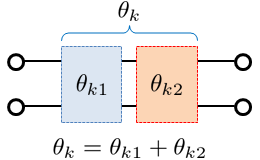
fig5.2 二分割されたT型回路の伝送量の関係
この関係を利用すると、ちょうど2分割されたときの抵抗R2とコンダクタンスG2は、以下のような式で計算することができます。 \begin{eqnarray} R_2 &=& Z_k \tanh \frac{\theta_k}{4} \tag{5.3} \\ G_2 &=& \frac{\sinh \theta_k / 2}{Z_k} \tag{5.4} \end{eqnarray}
ここで、前ページで扱っていた実例(R=2,G=1/4)を計算してみましょう。先の回路ではちょうど電圧・電流が半分になるという性質から \( \theta_k = \ln 2 \) の関係式がありました。 \( e^{\theta_k} = 2 \) から、 R は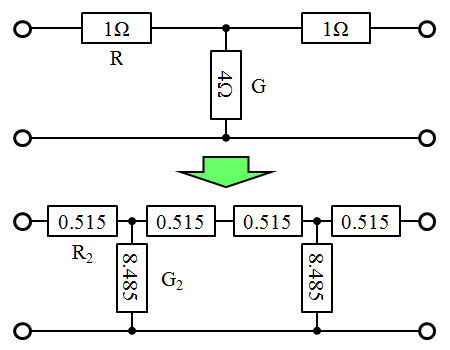
fig5.3 同一特性のまま2分割されたT型回路の定数計算結果
R と G はそれぞれピッタリ半分にはなりませんが、それに近い値となるという事実は、今後のさらなる分割を考慮するときの重要な性質といえます。
T型回路の分割数を増やす
さらに、同一特性を保つように多数のT型回路に分割した場合を考えていきます。分割数をnとおき、分割後のRとGをそれぞれ \(R_n\) と \(G_n\) で表せば、式(5.1)及び式(5.2)を流用することで、 \begin{eqnarray} R_n &=& Z_k \tanh \frac{\theta_k}{2n} \tag{5.7} \\ G_n &=& \frac{\sinh (\theta_k / n)}{Z_k} \tag{5.8} \end{eqnarray} として計算することができます。
ここで、幾つかのnの値で実際に数値計算してみると、以下のような抵抗値になります。
| 段数n | R | r | G=r/1 |
|---|---|---|---|
| 1 | 1Ω | 4Ω | 250mS |
| 2 | 514.7mΩ | 8.485Ω | 117.9mS |
| 4 | 259.3mΩ | 17.23Ω | 58.05mS |
| 8 | 129.9mΩ | 34.58Ω | 28.92mS |
| 10 | 103.9mΩ | 43.25Ω | 23.12mS |
| 100 | 10.40mΩ | 432.8Ω | 2.311mS |
| 1000 | 1.040mΩ | 4.328kΩ | 231.0μS |
| 10000 | 104.0uΩ | 43.28kΩ | 23.10μS |
以上の数値計算結果をみると、分割数nが大きくなるにつれて、ある係数に収束していくことが推測されます(一定値に収束するのは値ではなく、あくまで係数です)。 T型回路を分割していくほど、そのRは小さく(rは大きく)なっていくわけですが、その係数については、 1040 や 4328 といったある一定の値を示すのです。
これは双曲線関数 tanh や sinh の引数が、きわめて小さくなることによって生じる現象であり、 べき級数展開式を考えれば納得ができます。 \(B_n\) をベルヌーイ数として、 \begin{eqnarray} \tanh x & = & \sum^{\infty}_{n=1} (-1)^{n-1} \frac{2^{2n}B_n x^{2n-1}}{(2n)!} \\ & = & x - \frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315} \cdots \tag{5.9} \end{eqnarray} が正確なべき級数展開式ですが、 \(x\) が「十分に小さい」とすれば \[ \tanh x \simeq x \] と簡単な形に近似することができます。よって、分割数 n が大きい場合の \(R_n\) は、 \[ R_n \simeq Z_k \frac{\theta_k}{2n} \tag{5.10} \] という近似が可能です。
実際に、例示の回路を計算してみると、また \(\sinh\) も同様に、べき級数から考えると \begin{eqnarray} \sinh x & = & \sum^{\infty}_{n=1} \frac{x^{2n+1}}{(2n+1)!} \\ & = & x + \frac{x^3}{3!} +\frac{x^5}{5!} \cdots \tag{5.11} \end{eqnarray} であるので、結局のところ、極めて小さい \(x\) に対しては \[ \sinh x \simeq x \] が成立し、分割数 n が大きい場合の \(G_n\) は、式(5.12)で近似できることになります。 \[ G_n \simeq \frac{\theta_k}{n Z_k} \tag{5.12} \] 例示の回路においては、 \begin{eqnarray} G_n &=& \frac{\ln 2}{3n} \\ r_n &=& \frac{1}{G_n} = \frac{3n}{\ln2} \simeq 4.328n \ [\Omega] \end{eqnarray} の結果が得られ、こちらも表の数値と一致します。ただし、近似ですので、分割数nを十分に大きくする必要があります。
近似による計算誤差は、前提とする回路条件によって変わってきますが、例示の回路の場合、4分割で1%以下、100分割で6桁以下の計算誤差になります。
次ページへ続く