04.Ｔ型回路のＦパラ，反復インピーダンス及び伝送量

無限ラダーの要素としてのT型回路

前ページで、無限ラダー回路の重要な要素はT型回路であることが示唆されました。

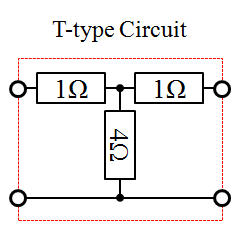
T-type Circuit

fig4.1 Ｔ型抵抗回路

図4.1は、抵抗減衰器(Attenuator)としてよく知られている回路で、その性質や設計法に至るまで、よく研究された回路の一つです。

本回路は左右が対称であることから、「対称２端子対網」と呼ばれ、比較的容易にその諸性質が割り出せる回路となっています。ここからは、その詳しい性質を調べていきましょう。

T型回路のFパラメータ(縦続行列)

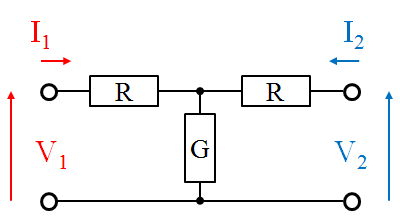
T-type Circuit2

fig4.2 T型抵抗回路の電圧電流

fig4.2は一般的な表現の対称T型回路です。これまでと異なるのは、回路に並列に入ってるGの要素を抵抗ではなく、その逆数であるコンダクタンスで表現していることです。まずはこの回路のF行列と呼ばれる定数を求めていきます。この定数は別名がたくさんある定数です。

日本ではFパラメータ (Fundamental: 基礎定数)や「四端子定数」または縦続行列 (cascade parameter)と呼ばれることが多いもので、他には chain-parameter (チェーン)やドイツ語のチェーンに由来する「K行列」 (Kettenmatrix)、あるいは伝送線路パラメータ (Transmission Line parameter )、最近の英語圏ではABCD-parameter などと、様々な呼称が存在します。

このパラメータは、回路網を数珠つなぎに接続したときに、総合的な特性を求めやすい表現であり、過去には非常に重視された回路網定数であったためなのか、様々な名称が乱立してしまったようです。

さて、ここではFパラメータ(F行列)という名称を選択しておきましょう。このパラメータは以下で定義されます。（ただし、符号の向きなどが異なる別の定義あり。）

\[ \left( \begin{array}{c} V_1 \\ I_1 \end{array} \right) = \left( \begin{array}{cc} A & B \\ C & D \end{array} \right) \left( \begin{array}{c} V_2 \\ -I_2 \end{array} \right) \tag{4.1} \]
あるいは、連立方程式で表して、
\begin{eqnarray} V_1 &=& A V_2 -B I_2 \\ I_1 &=& C V_2 -D I_2 \tag{4.2} \end{eqnarray}
でも構いません。そして、途中を端折って fig4.2 の Fパラ結果だけを出せば、 \begin{eqnarray} A &=& RG+1 \\ B &=& R^2G+2R \\ C &=& G \\ D &=& RG+1 \tag{4.3} \end{eqnarray} となります。（なお、左右対称の回路の場合、必ず \(A=D\) となる。）。 これらの値を使えば回路の諸性質…インピーダンスや、電圧電流の減衰比率（伝送量）を容易に求められます。

もし fig4.1 の回路定数であれば、 R=1[Ω] G=1/4 [S] として、 \begin{eqnarray} A =D &=& \frac{5}{4} \\ B &=& \frac{9}{4} \\ C &=& \frac{1}{4} \end{eqnarray} という値になります。なお、 \(A,D\) は無単位の量であり \(B\) は抵抗の物理単位、 \(C\) はコンダクタンスの物理単位を持ちます。

T型回路の反復インピーダンス

Fパラメータが求められたので、重要な量の一つである、反復インピーダンス (iterative impedance) を求めてみます。

この反復インピーダンスというのは、無限に回路をつなげていった時の入力抵抗（インピーダンス）のことです。つまり、無限ラダー回路で求めた合成抵抗値の正式名称です。

「反復」というのは「繰り返し」の意味合いが強く、無限に接続した回路なので、どの点から見ても同じインピーダンスに見える＝繰り返されている、ことを言いたいのです。

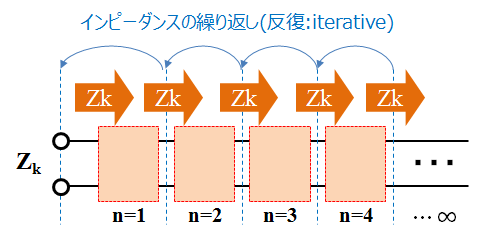
iterative impedance

Fig4.3 反復インピーダンス(Iterative Impedance)

Fig4.2 は対称２端子対回路なので左右方向の反復インピーダンスは一致し、値は簡単に求まります。 その反復インピーダンスを \(Z_k\) とおけば、以下の算出式(4.4)となります。

\[ Z_k = \sqrt{\frac{B}{C}} = \sqrt{R^2 + \frac{2R}{G}} \tag{4.4} \]

実際に Fig4.1 の定数 \(R=1,G=1/4\) で計算してみましょう。

\[ Z_k = \sqrt{1^2 + \frac{2 \times 1}{1/4} } = \sqrt{9} = 3 \Omega \] ちゃんと最初に計算した “Ｔ型回路が無限に縦続接続された回路の合成抵抗値” と一致することが確認できます。

T型回路の伝送量(減衰度)

次に計算するのは、各段の減衰量です。入力電圧及び入力電流が、どの程度減衰して出力されるかといった量です。

実際 Fig4.1 の回路は、1段ごとに電圧と電流はちょうど 1/2 に減少します。

この減衰量のことを回路理論上は「伝送量」と表現することが多く（増幅などもあるため）、指数関数を用いて \[ \frac{V_2}{V_1} = e^{-\theta_k} \tag{4.5a} \] または、 \[ \ln \frac{V_1}{V_2} = \theta_k \tag{4.5b} \] のように定義されており、特に \(\theta_k\) を「伝送量」と称しています。

なお、当然のことながら電流についても伝送量が定義されるのですが、反復インピーダンスの前提があるため、電圧と電流の比率は常に一定となっています。ですから電圧の伝送量と一致することになり、あらためて電流の伝送量を考慮する必要はありません。

　Fパラメータによって伝送量を求めるには、双曲線関数(ハイパボリックsin等)を使用します。sinh 関数の定義を 式(4.6)に示します。 \[ \sinh x = \frac{e^x-e^{-x}}{2} \tag{4.6} \] 次に伝送量 \(\theta_k\) と Fパラメータ の関係を式(4.7)、回路定数の関係を式(4.8)に示します。（導出などの詳しくは電気回路の教科書を参照のこと。）
\begin{eqnarray} \sinh \theta_k &=& \sqrt{A^2-1} = \sqrt{BC} \tag{4.7} \\ &=& \sqrt{R^2 G^2 + 2 RG } \tag{4.8} \end{eqnarray}
このままでは \(\theta_k\) を求められないので、sinh関数の逆関数を利用してFパラメータから伝送量を計算してあげます。逆双曲線正弦関数の定義は次式(4.9)です。
\[ \sinh^{-1} x = \ln \left(x+\sqrt{x^2+1} \right) \tag{4.9} \]
これを使って結果を求めるならば
\[ e^{\theta_k} = \frac{V_1}{V_2} = \sqrt{R^2 G^2 + 2 RG } + RG + 1 \tag{4.10} \]
という式に帰着します。もし、Ｆパラメータで表現するならば、 \[ \frac{V_1}{V_2} = A + \sqrt{A^2-1} \] ということです。 試しに Fig4.1 の回路定数を 式(4.10) へ代入してあげれば \( A = RG =1/4 \) から
\begin{eqnarray} \frac{V_1}{V_2} &=& \sqrt{\frac{1}{16} +\frac{2}{1} } + \frac{1}{4} + 1 \\ &=& \frac{3}{4} + \frac{5}{4} \\ &=& 2 \tag{4.11} \end{eqnarray}
となって、ちょうど電圧・電流が半分になることが再確認できました。

式(4.11) を伝送量 \(\theta_k\) で表すならば、 \[ \theta_k = \ln 2 \tag{4.12} \] という表現になります。

次ページへ続く