03.無限抵抗ラダーの対称性と構成要素２

前ページで、対称性の良い抵抗ラダー回路に書き換えることにしましたが、最初に調べていた抵抗ラダーとはやや違いがあります。

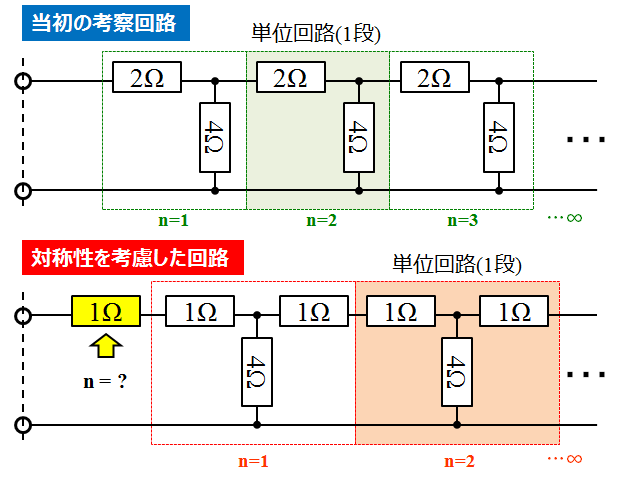
上の図の上下の回路は、全く同じ回路ですが、対称回路の方は、余計な抵抗が１個付加されることになってしまいます。

このn=0段目に相当する、黄色の1Ωが対称性を悪化させていた張本人です。実際、この事は合成抵抗値を求める式(1.8)にも、こっそり現れていました。 \begin{eqnarray} Z_\infty &=& \frac{R}{2} + \frac{\sqrt{R(R+4r)}}{2} \tag{1.8} \\ &=& 1 [\Omega] + 3 [\Omega] = 4 [\Omega] \end{eqnarray}

つまり、対称的な無限抵抗ラダーの合成抵抗値は3[Ω]であり、それに直列に1Ωをつないだのが、最初の考察回路ということです。そういう理由があって、右を見たときは 3+1=4Ω 左を見たときは 3-1=2Ω と異なった合成抵抗値を示したのでした。

図で表せば、下図のようになります。

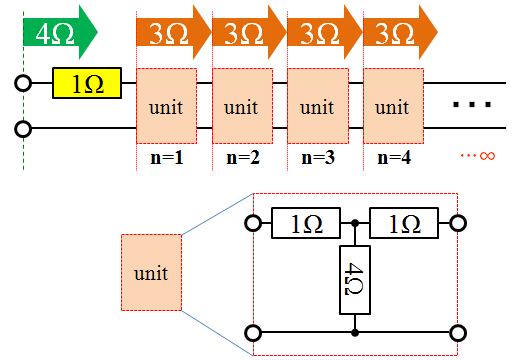
この回路は、任意の段から右方向を見た抵抗値が常に3Ωであり、無限に繰り返されることになります。唯一違うのは左端から見たときに4Ωとなることだけです。

以上の考察から、「左右対称性を重視」した「無限段」のラダー回路においては、3本の抵抗でつくられたＴ型回路が主役であり、その特性が、ラダー回路の基礎的な性質を担っていることを示しています。（もしくは3本の抵抗でできたπ型回路を主役にする事も出来る）

次ページへ続く