無限抵抗ラダーの対称性と構成要素1
はじめに
前ページでは、無限に続く抵抗はしご回路(抵抗ラダー)の抵抗値をどう求めるかを扱いましたが、ここでは、その回路がどのような回路構成であると捉えるべきかを考えていきます。
無限段抵抗ラダーの対称性
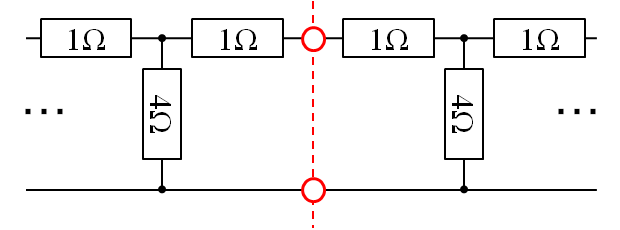
以下の図の定数をもった無限段の抵抗ラダーの総抵抗値は、\( Z_\infty \)は 4 Ωであることが分かっています。この場合、R=2Ω,r=4Ω(またはコンダクタンス表現でG=0.25S)です。
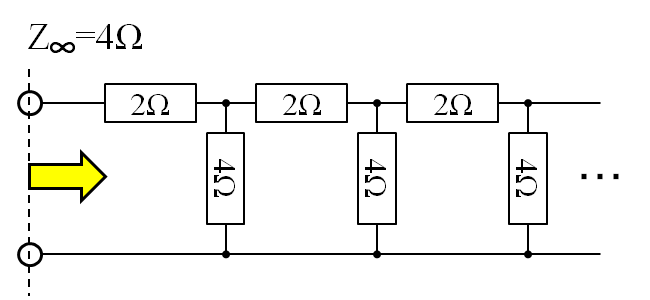
この回路定数である限り、各段ごとに電圧電流はそれぞれ1/2づつ減衰し続ける特性があり、任意のn段目の電圧と電流の比率Znは \[ Z_n=\frac{V_n}{I_n}=4 [\Omega] \tag{2.1} \] と固定的です。
ここで、今まで扱ってきた「無限段ラダー」という対象の意味を考えてみると、今考えているのは片方向に無限に続く回路のことであって、これを両側へ向かってどこまでも続く「両方向無限段ラダー回路」に拡張することも当然できることに気付きます。
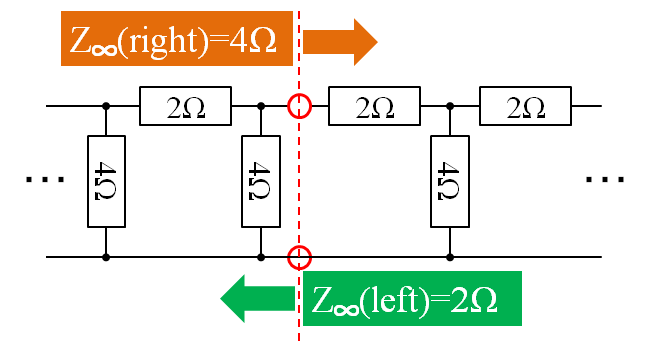
ところが、両方向無限大ラダー回路では、任意の中間点で回路を切断しようとすると、左右の方向次第で測定される合成抵抗値が変わってしまう問題が出てきてしまうのです。
同じように、切断箇所をずらしてみても、やはり左右方向の測定値が変わります
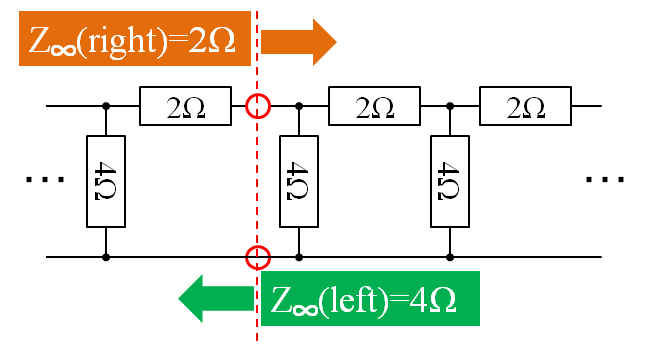
要するに、この回路は対称性が悪いのです。左右に関係なく同じ特性を持ったラダー回路のはずであるのに、異なった合成抵抗値を示すのは、どことなく違和感を感じないでしょうか。
この事自体は決して回路的に間違いではありません。ですが、無限に続く回路なので「任意の場所で切断」しても「左右方向の特性が同じ」であった方が、より適切な回路網表現であると言えるでしょう。
そこで、対称性の良い回路へ書き換えられないか、という考えに至るわけです。
対称性の良い無限段抵抗ラダー回路
回路の対称性を尊重したい場合、左右に切断する箇所を工夫すればよいことになります。2種類の方法がありますが、ここでは、抵抗Rを真っ二つに切断するとします。(もう一つの方法は、4Ωの抵抗を8Ωの抵抗2つに分割する手法です。)
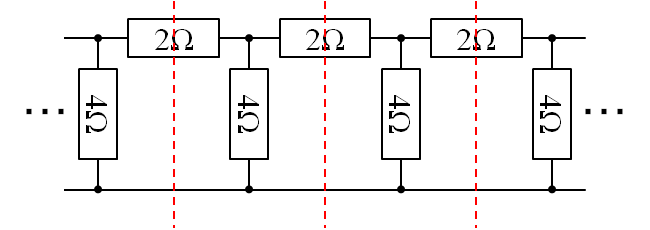
このように2Ωの抵抗を2つの1Ωの抵抗となるように切断すれば、左右対称の回路特性となります。
あくまで無限大ラダーに限ってという注意事項はありますが、回路の要素(ラダーの1段)は、下図のように書き換えられたことになります。
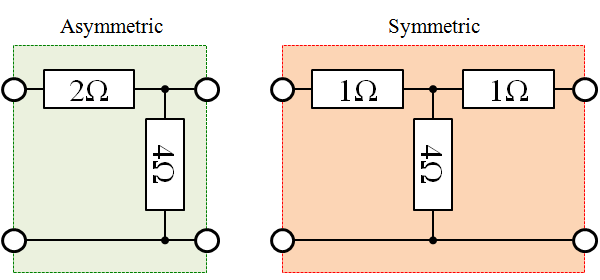
次ページへ続く