無限抵抗ラダー回路
はじめに
本テキストは、15年ぐらい前に書いたまま放置していたのを、最近書き直してみたものです。分布定数回路の説明をするのに、直流でやった方が分かり易いはずと考えてやってものの中途半端なままにしてありました。
とはいえ、修正の気合はあまり入っていないので、当面、昔の雰囲気を引きずったままにしてあります。
抵抗ラダー(はしご)回路
抵抗ラダー回路とは、図のように抵抗をはしご状に接続した回路のことです。分布定数回路の直流版のような回路です。
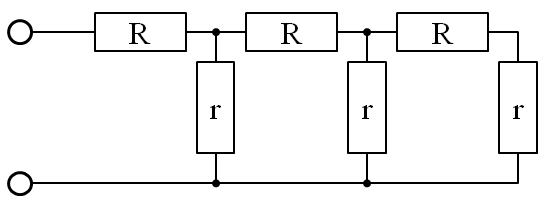
1段ずつ増やしていくことで、この回路がどのような抵抗値を持つのか調べてみます。では、早速始めてみましょう
1段のときの全抵抗
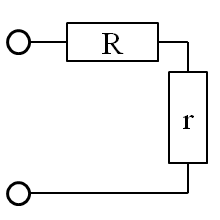
ラダーが1段しかない、図2の回路においては、
2段のときの全抵抗
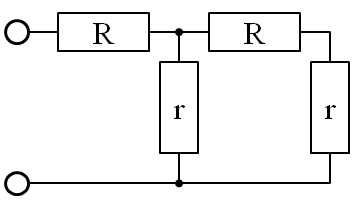
2つの抵抗が並列接続されたときは、それぞれの抵抗の積÷抵抗の和の公式が成り立つので、
これは、前の全抵抗に一段ラダーを付加したと考えられるので、回路図を整理してみると
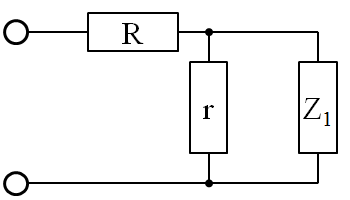
3段のときの全抵抗
2段の場合と同じように、前の抵抗をつなげると考えれば、
n段のときの全抵抗
抵抗ラダー回路の全抵抗Znは、段数nが増えるに従い、ある一定値に収束していきます。 たとえば、R=2[Ω] 、r=4[Ω]を計算してみたのが以下の表です。
| 段数 | 全抵抗値(Ω) |
|---|---|
| \(Z_1\) | 6.00000000 |
| \(Z_2\) | 4.40000000 |
| \(Z_3\) | 4.09523810 |
| \(Z_4\) | 4.02352941 |
| \(Z_5\) | 4.00586510 |
| \(Z_6\) | 4.00146520 |
| \(Z_7\) | 4.00036623 |
| \(Z_8\) | 4.00009155 |
| \(Z_9\) | 4.00002289 |
| \(Z_{10}\) | 4.00000572 |
| \(Z_{11}\) | 4.00000143 |
| \(Z_{12}\) | 4.00000036 |
| \(Z_{13}\) | 4.00000009 |
| \(Z_{14}\) | 4.00000002 |
無限ラダー回路
では、段数 \(n\)が無限大になった時の抵抗ラダー回路はどのような抵抗値Zになるのでしょうか。
アプローチの一つ目は、式(1.9)を使って極限を取る事です。変数の \(k\) は、\(R \gt0 \) 及び \(r \gt 0\) の条件では必ず \( k \gt 1\) になるので段数 \(n\) の極限で収束します。
もう一つのアプローチは、段数nが無限大の時には既に抵抗値が収束していると仮定し、それに、もう一段のラダー回路を付け加えても抵抗値に変化があるはず無いと考える方法です。こちらの方が直感的に分かりやすい。
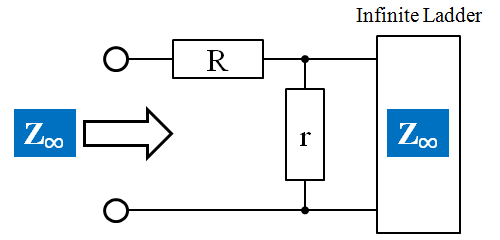
先にやってみた\( R=2\mathrm{[\Omega]} , r=4\mathrm{[\Omega]}\) の場合では、 \(Z_\infty\) がちょうど4Ωに収束する計算となり、シミュレーションが収束していく値と一致している事がわかります。
次ページへ続く
補足A1.抵抗ラダーの一般式の求め方。
漸化式(1.6)を、一般分数型の形で表現すると、
\[
a_{n+1}=\frac{r a_n+s}{p a_n +q} \tag{1.A1}
\]
ここで、 \( a_{n+1}=a_n=x \) と置いて(実はここで収束仮定している。)、特性方程式を立てると
\[
px^2+(q-r)x-s=0 \tag{1.A2}
\]
式(1.A2)の解をそれぞれ \( \alpha,\beta \) とし、重解ではないとする。(ただし、抵抗ラダーの条件で計算すれば重解にならない)
そして、テクニック的に
\[
a_{n+1}-\alpha \tag{1.A3}
\]
及び
\[
a_{n+1}-\beta \tag{1.A4}
\]
を計算する。式(1.A3)は、
\begin{eqnarray}
a_{n+1}-\alpha &=& \frac{(ra_n+s)-(p a_n+q)\alpha}{pa_n+q} \\
&=& \frac{(r-p\alpha)a_n+s-q\alpha}{pa_n+q}
\end{eqnarray}
(1.A5),となるが、\( s-q \alpha\)は、式(1.A2)より、
\[
s-q\alpha=-\alpha(r-p\alpha) \tag{1.A6}
\]
と書き換えることができる。なぜなら式(1.A2)に解の一つαを代入すれば、
\begin{eqnarray}
p \alpha^2+(q-r)\alpha-s \\
p \alpha^2 +q\alpha -r \alpha -s =0 \\
s-q\alpha =-\alpha(r-p\alpha)
\end{eqnarray}
と計算でき、上手い形がつくれるからである。
式(1.A5)を式(1.A6)を使って書き換えると、
\begin{eqnarray}
a_{n+1}-\alpha
&=& \frac{(r-p\alpha)a_n+s-q\alpha}{pa_n+q} \\
&=& \frac{(r-p\alpha)a_n - \alpha(r-p\alpha)}{pa_n+q} \\
&=& \frac{(r-p\alpha)(a_n-\alpha)}{pa_n+q} \tag{1.A7}
\end{eqnarray}
,といった、分子を積の形にまとめることができる。同様に、
\[
a_{n+1}-\beta = \frac{(r-p\beta)(a_n-\beta)}{pa_n+q} \tag{1.A8}
\]
さて、式(1.A7)及び式(1.A8)は分母を同じにしたので、式(1.A7)を式(1.A8)で割ることにすれば、
\[
\frac{a_{n+1}-\alpha}{a_{n+1}-\beta} = \left( \frac{r-p\alpha}{r-p\beta} \right) \frac{a_n-\alpha}{a_n-\beta} \tag{1.A9}
\]
と、等比数列の形に変換ができる。ここに、
\[
b_n = \frac{a_n-\alpha}{a_n-\beta} \tag{1.A10}
\]
と定義すれば、
\[
b_{n+1} = \left( \frac{r-p\alpha}{r-p\beta} \right) b_n \tag{1.A10}
\]
となって、bnは公比 \( (r-p\alpha) /(r-p\beta) \)の等比数列になっていることが分かる。式(1.A10)の初項\(b_1\)は、
\[
b_1 = \frac{a_1-\alpha}{a_1-\beta} \tag{1.A11}
\]
であり、初項a1さえ既知であれば \(b_n\) を一般的な形に書くことが出来て、
\[
b_n = b_1 \left( \frac{r-p\alpha}{r-p\beta} \right)^{n-1} \tag{1.A11}
\]
式(1.A11)の公比は \(n\) に依存しない定数になっているので、これ以降 \(k\) とおく。つまり、
\[
b_n = b_1 k^{n-1} \tag{1.A12}
\]
とする。この関係から \(a_n\) を求めることができて、
\[
\frac{a_n-\alpha}{a_n-\beta} = b_1 k^{n-1}
\]
を \(a_n\) について解けば
\[
a_n = \frac{\beta b_1 k^{n-1}-\alpha}{b_1 k^{n-1}-1} \tag{1.A13}
\]
が目的であった \(a_n\) の形式となる。さらに、実際の式(1.6)に当てはめるには、
\begin{eqnarray}
r & \longrightarrow & R + r \\
s & \longrightarrow & Rr \\
p & \longrightarrow & 1 \\
q & \longrightarrow & r
\end{eqnarray}
と置換し、面倒な諸計算を行うと
\[
k = b_1 = \frac{r+\beta}{r+\alpha}
\]
となるので、
\begin{eqnarray}
a_n & = & \frac{\beta b_1 k^{n-1}-\alpha}{b_1 k^{n-1}-1} \\
& = & \frac{\beta k^{n}-\alpha}{k^{n}-1}
\tag{1.7}
\end{eqnarray}
が導ける。また各変数を再掲すれば、
\[
\alpha = \frac{R}{2} - \frac{\sqrt{R(R+4r)}}{2} \tag{1.7.1}
\]
\[
\beta = \frac{R}{2} + \frac{\sqrt{R(R+4r)}}{2} \tag{1.7.2}
\]
\[
k = \frac{r+\beta}{r+\alpha} \tag{1.7.3}
\]
となる。
次ページへ続く
漸化式(1.6)を、一般分数型の形で表現すると、
次ページへ続く