6.ダランベールの解の性質

ここでは、前ページのダランベールの解(d'Alembert's solution)が一体どのような性質の方程式なのかを具体例で説明します。

ダランベール解というのは、実は、１次元の線上（方向）を波動が伝わっていく様子を表す「波動方程式」の一種なのですが、けっこう抽象的な式であるために、「波動」であることが見えにくいと思います。

方程式は $f(x-ut),g(x+ut)$ の二つの関数の和で表されていますが、そのうち片方の関数 $ f(x-ut) $の性質から調べていくことにしましょう。

ここで、ダランベール解の一部$ f(x-ut) $を満足する方程式を考えます。例えば次の式(6.1)は $ x-ut $ の項を含むので、条件を満足しています。 \[ f(x,t)=e^{-\alpha (x-ut)^2} \tag{6.1} \]

これでも具体的な関数ではあるのですが、より具体性をもたせるために、距離単位をメートル(x[m])、時間単位を秒(t[s])としましょう。変数もそれぞれα=0.1、u=2としてみます。まとめて \[ f(x,t)=e^{-0.1 (x-2t)^2} \tag{6.2} \]

２変数のままでは少し分かりにくいので、時刻t=0[s]の特殊な場合を考えてみると、図5-1のようにx=0[m]で最大値1[V]の値を示すパルス波形（ガウシアンパルス）になります。

図5-1 t=0秒のときの波形

ここで、波形の最大値に注目してみます。波形が最大になる条件は、図5-1では距離0[m]ですが、式(6.1)を考えると、eの肩が0になること、すなわち \[ x-ut=0 \] であることは明らかです。

関数 $f(x,t)$ が最大値を取る $x$ の値を $x=x_{max}$ として時間tを増やしていったときに、 $x_{max}$ はどう変化するでしょうか。0秒は上のグラフで見ていますので、時間tを5秒後、そして10秒後にすると、 \begin{eqnarray} & t=5 : & x_{max}-2 \times 5 =0 \\ && \Rightarrow \hspace{1em} x_{max}=10 \\ \\ & t=10: & x_{max}-2 \times 10 =0 \\ && \Rightarrow \hspace{1em} x_{max}=20 \end{eqnarray} つまり、5秒後に最大電圧値を取るxは10[m]の位置、10秒後では20[m]の位置となります。図5-2はその様子を示したグラフです。

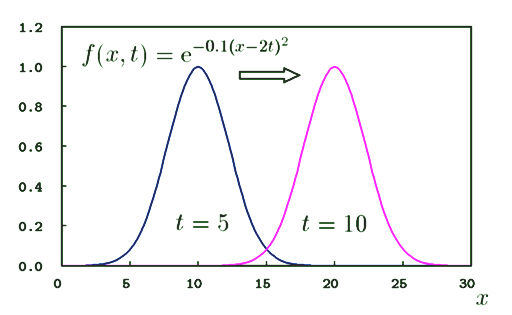
図5-2 時間を増加したときの波形の推移

このように時間tが増えるにしたがって、ピーク値を取る $x_{max}$ も右へ移動していきます。すなわち、パルスが$x$軸方向に進行している様子を表しています。そのため$f(x-ut)$の項は進行波と呼ばれています。

その速度sも上記の例から算出することができ、 \[ s=\frac{\Delta x}{\Delta t}= \frac{20-10}{10-5}= 2 \mathrm{[m/s]} \] これは、最初に設定したuそのものです。

$f(x-ut)$という関数においてuは波の速度を表すのです。

もっと直接的に速度を求めるならば、 $x-ut $ がある値の場所に着目します。上の例では、値がゼロとなる場所を追うことになるのですが、言い換えれば「波高が同一（等位相）」の点を追いかけていることなので、それを仮にKとおき、$ x-ut=K $とします。そして、その両辺をtで微分するならば、 \[ \frac{dx}{dt}-u =0 \hspace{1em} \Rightarrow \hspace{1em} \frac{dx}{dt}=u \] が導かれます。 ここで、$dx/dt$、すなわち距離の時間微分は「速度」そのものですので、uが速度を意味することが直ちに分かります。以上で、直接的に波動の速度が求まりました。

無損失線路の速度uの内訳は \[ u= \frac{1}{\sqrt{LC}} \] でした。

その速度は、伝送線路の単位長あたりのCとLが小さいほど速くなることが分かります。逆に誘電率の高い絶縁体や透磁率の高い配線材料を使うほど、速度はどんどん遅くなり、光速の半分ぐらいになったりすることもあります。

それとは逆に、速度を上げるためには、可能な限り線路のCやLを小さくすればよいことになります。そして高性能な同軸ケーブルほどLやCが小さい傾向があったりします。

しかしながら、CやLを小さくするのには物理的な限界があり、真空の誘電率$ \epsilon_0 $や真空の透磁率$\mu_0 $がそれぞれの限界点となります。もちろん、一般的にというただし書きは付くでしょうが。

（参考：透磁率 $ \mu $ の単位はヘンリー/メートル[Henry/meter]で、分布定数回路のLの単位[H/m]と同じ。また誘電率 $ \epsilon $ の単位もファラッド/メートル[Farad/meter]でCの単位[F/m]と同じです。）

その限界速度とは、以下の式…すなわち光の速度です。 \[ c= \frac{1}{\sqrt{\epsilon_0 \mu_0}} \]

このように計算された速度は、波の位相が一定の点に着目した速度なので位相速度(phase velocity)と呼ばれています。位相速度は、「波形」の速度であり、エネルギや信号を運ぶ速度とは必ずしも一致しません。

そのため、これとは別に群速度(group velocity)と呼ばれる速度の指標もよく用いられます。群速度はごく近い周波数の正弦波を２波以上伝送路に流した時にできる包絡線波形の速度です。無線工学的にいえば、ＡＭ変調したときの波形が伝送路上を流れる速度です。TEM波では一般的に位相速度と群速度はだいたい同じ値をとります。（補足）

もう一つの関数$ g(x+ut) $は、$ f(x-ut) $と全く同じ解の形になりますが、波の進行方向が逆になるだけです。計算は各自でしてみてください。

こちらの方は、実務上「反射波」と呼ばれることの多い波動です。それ以外には、単に「進行波」と呼ばれてみたり、「負の方向への進行波」と区別したり、「後退波」と呼ばれてみたり、いろいろな名前で呼ばれがちです。

式(4.2)が速度の単位をもつことは説明しましたが、直感的にはとてつもなく分かり難いのではないでしょうか。正直、電気回路に馴染んでいるとLとCで速度が出るとは何とも思いつかないモノです。

もしMKSA単位から、直接算出すると以下のようになります。 \[ L: \frac{\mathrm{Henry}}{\mathrm{meter}} \Rightarrow \frac{\mathrm{m \cdot kg}}{\mathrm{s^2 \cdot A^2}} \] \[ C: \frac{\mathrm{Farad}}{\mathrm{meter}} \Rightarrow \frac{\mathrm{s^4 \cdot A^2}}{\mathrm{m^3 \cdot kg^2}} \] \begin{eqnarray} u &=& \frac{1}{\sqrt{LC}} \\ &=& (LC)^{-1/2} \\ &=& \left( \frac{\mathrm{m \cdot kg}}{\mathrm{s^2 \cdot A^2}} \times \frac{\mathrm{s^4 \cdot A^2}}{\mathrm{m^3 \cdot kg^2}} \right)^{-1/2} \\ &=& \left( \mathrm{s^2/m^2} \right) ^{-1/2} \\ &=& \left( \mathrm{s/m} \right)^{-1} \\ &=& \mathrm{m/s} \end{eqnarray}

まぁ、確かに速度の単位になっています。ここでは通常の集中定数素子のLやCの単位と異なることに注意してください。あくまで単位長あたりのインダクタンスとキャパシタンスになるので[m^-1]だけ違いが出てきます。

直感的に分かりやすいのは、LC共振回路の共振周波数の有名な式でしょうか。 \[ f=\frac{1}{2\pi \sqrt{LC}} \]

この式は分布定数回路の速度とほとんど同じです。ただし集中定数素子の公式ですのでLとCの単位が異なります。

公式の単位は周波数、すなわち時間の逆数なので[s^-1]の次元を持つことが分かります。もし式中のL、Cを分布定数の単位に置き換えると、[m]の次元が新たに増え、最終的な組み立て単位は[m・s^-1]となり、速度の単位になることが確認できます。

電気回路になじんでいる方なら、こちらの方が分かりやすいのではないでしょうか。

このあたりの「波の速度」に関する議論はかなり難しいもののようです。

分布定数回路理論は主にTEM伝送路を扱うため、位相速度も群速度もだいたい同じとみなしても問題は無いのですが、かつては物理学の観点から大きく問題が提起され、今でも重要なテーマになっているようです。

まず導波管について例を挙げると、電磁波の位相速度と群速度がまったく異なります。さらに、位相速度は光速度を超えてしまうのです。 しかしながら、導波管内の群速度は光速度以下になるため、群速度が一般にエネルギーや信号を伝送する速度とみて差し支えありません。

ところが、異常分散媒質とよばれる伝送路条件になると、群速度であっても光速を超えるときがあります。はたまた負の群速度というのも現れたりもします。このような特殊な条件になると、群速度ですら速度の指標になりえないのです。

異常分散媒質のよく知られた例としては、電離層内での伝搬があげられます。他に大昔の電話用架空裸線にもそのような条件がありました。

1914年、ゾンマーフェルト(A.Sommerfeld)とブリュリアン(L.Brillouin)がAnnalen der Physik誌で群速度は真の伝搬速度とは言えないこと、いかなる伝送路であっても真空中の光速度より早くは伝搬しないことを厳密に証明するまで、上記の問題はアインシュタインの特殊相対性理論（1906年）への反証へ使われていたぐらいデリケートな問題でした。

これ以降は、波の速度の指標に信号速度(signal velocity)や先端速度・波頭速度(front velocity)という概念も現れ、特に先端速度は真空中の光速度以上にはなれないことが証明されたため、特殊相対性理論と矛盾する心配が無くなったのです。