検波器の入力インピーダンスってどのぐらい？

（最初）に戻る

はじめに

これまでは、ダイオード検波器の入出力特性を中心に解析していましたが、その前提は内部抵抗ゼロ、電力無尽蔵の理想電圧源を使うことでした。

実際には有り得ないどころか、ゲルマ／鉱石ラジオにあっては最も厳しい条件で奮闘せざるを得ませんので、現実とのギャップがトンデモないことになります。

具体的にいえば、現実の電源インピーダンスが100kΩオーダという過酷な条件ということであり、十分なレベルのＲＦ入力電圧を確保できても、検波器をつないだ途端に強烈な電圧降下に見舞われます。その結果、出力は雀の涙…ということですね。

そこで、本ページでは電圧降下を決定する最大の要因である、入力インピーダンス（以下、入力Ｚまたは$Z_{in}$）について紹介していきます。

大雑把な把握

解析する回路網は、図１のようなものを想定します。正弦波入力$v_i$があり、DC電圧$V_o$が出力されています。

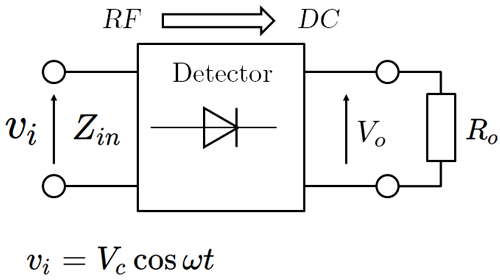
図１．ダイオード検波器の回路網モデル

このときの入力インピーダンス $Z_{in}$ は非線形抵抗成分であって、信号レベルにより大きく変化するのですが、回路で消費される全電力を$P_{in}$として、

\[ Z_{in} = \frac{V_c^2}{2 P_{in}} \]

として定義される量になります。正確には等価入力抵抗と呼ぶべきものです。

単純な導出によるもの

もっとも単純な計算によれば、入力インピーダンス$Z_{in}$は式(1)で表されます。

\[ Z_{in} = \frac{R_o}{2} \tag{1} \]

つまり、入力インピーダンスは出力抵抗Roの半分。ただし、入力が十分に大きい必要があり、具体的には0.3V以上のRF入力が欲しいところです。

この式は入力と出力のパワーが等しいと置くことによって求められ、

\[ \frac{V_c^2}{2 Z_i} = \frac{V_o^2}{R_o} \]

から、

\[ Z_i = \frac{R_o}{2} \frac{V_c^2}{V_o^2} \simeq \frac{R_o}{2} \]

として、入力の振幅と出力電圧がほぼ等しい（検波器の損失が無視できる）として近似したものです。

もう少し近似度をあげたもの

上記の式において、近似度を上げたものです。

\[ Z_i = \frac{R_o}{2\eta} \tag{2} \]

ここで、$\eta$は電圧の観点から見た検波効率(0～100%)で、式(3)によって定義されます。

\[ \eta = \frac{V_o}{V_c} \tag{3} \]

式(2)では、小信号領域での近似度が式(1)よりも改良されています。

導出にあたっては入力が十分強いとし、入力振幅が波高値$V_c$付近になったときの $\Delta t$ 秒だけ、ダイオードにパルス状の電流$i_p$が方形波的に流れるものと仮定します。

これは、出力電圧$V_o$がダイオードに対して逆バイアスとなっているためで、$V_c \cos \theta$が$V_o$を超えた時だけ電流が流れることを近似したものです。

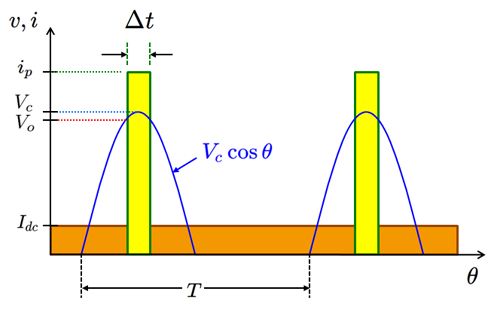
図２．ダイオード検波器のパルス電流仮定

パルス状電流が流れているときの瞬時入力電力$P_{peak}$は、$V_c \cos \theta$があまり変化しないタイミングであるので、

\[ P_{peak} = V_c \ i_p \]

として扱うことができます。入力電力$P_{in}$は瞬時パワーを時間平均したものなので、$T$を交流１周期の時間として

\[ P_{in} = V_c \ i_p \frac{\Delta t}{T} \]

となります。

ところで、この式中にある $i_p \Delta t/T $という量は、負荷抵抗 $R_o$ に流れる直流電流値 $I_{dc}$ に他なりません。なぜなら電荷量保存の法則から、

\[ Q = i_p \Delta t = I_{dc} T \]

が成立しているので、パルス電流の平均値が出力の直流電流値に等しくなくてはいけないのです。

よって入力電力P_inは

\[ P_{in} = V_c \ i_p \frac{\Delta t}{T} = V_c I_{dc} = V_c \frac{V_o}{R} = \frac{\eta V_c^2}{R} \]

と書く事もできて、これを入力インピーダンスの定義式に代入すれば、

\[ Z_i = \frac{V_c^2}{2 P_{in}} = \frac{V_c^2}{2 \eta V_c^2/R}= \frac{R}{2 \eta } \]

となるわけです。

古典理論による厳密解

ダイオードが指数特性ではなく、線形特性を持つと仮定した古典的な解析式です。

\[ Z_i = R_o \ \frac{\tan \theta -\theta}{\theta-\sin \theta \cos \theta} \tag{4} \]

ここで、突然出てきたθは、検波効率 $\eta$ に関係する値であり式(5)で定義されます。（詳しくは、ダイオードのターンオン時間を位相角で表現したもの。導通角とか流通角とか呼ばれる量。）

\[ \cos \theta = \eta = \frac{V_o}{V_c} \tag{5} \]

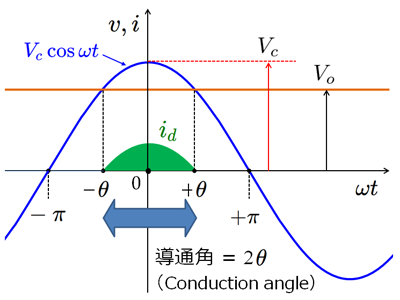
図３．導通角の説明

ダイオードが線形特性を持つと仮定すると、V-I特性グラフは図４のようになります。Ｇｅダイオードや鉱石検波器は、抵抗成分が比較的大きく、十分な入力レベルが確保できれば図３のように近似しても差し支えなかったりします。本式は真空管（２極管）時代に使われた式です。

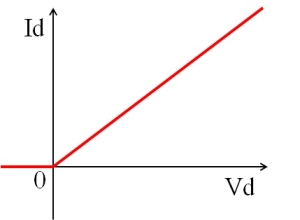
図４　ダイオードの線形近似グラフ

式（４）は、式（２）と比べて、さほど変わらない値が出るので、面倒な割には使いにくい式だと感じています。結局のところ、θがゼロに近く検波効率が良い場合には、

\begin{eqnarray} \frac{\tan \theta -\theta}{\theta-\sin \theta \cos \theta} &=& \frac{1}{\cos \theta} \cdot \frac{\sin \theta - \theta \cos \theta }{\theta-\sin \theta \cos \theta} \\ & \approx & \frac{1}{2 \cos \theta} \\ & =& \frac{1}{2\eta} \end{eqnarray}

と近似できてしまうことによります。しかも、θが$\pi/2$に近い場合でもほとんど変化がありません。

上記の式についての導出過程や性質を知りたい方は、こちらの補足資料をご覧ください。

指数関数特性の厳密解

ダイオード電流式をそのまま解いたのが式(6)です。これが最も現実に近い（と思われる）値となります。一番複雑な形をしているのは残念な部分です。

\[ Z_i = \frac{V_c}{2(I_s+ I_{dc})} \cdot \frac{{f_0}(V_c/V_T)}{{f_1}(V_c/V_T)} \tag{6} \]

ここで、各変数は

$V_c$: 入力ＲＦ振幅電圧[V]
$V_T$: ダイオードの熱電圧[V]（約26mV）
$I_s$: ダイオードの逆方向飽和電流[A]
$I_{dc}$: 回路内ＤＣ電流[A] $ =V_o/R_o$
$f_0$: 第１種０次変形ベッセル関数
$f_1$: 第１種１次変形ベッセル関数

特殊関数である変形ベッセル関数は、数学の世界で $I_0,I_1$ といった記号が標準的ですが、電流 $I$ と紛らわしいので、代替的に $f_0(x)$ と表記しています。

式(6)の最も特徴的なことは、微小入力時のインピーダンスが正確に出ることです。式(2),(4)では、微小入力時のZiが極めて大きい値になってしまうのですが、本式を使うと、ダイオードの動抵抗（微分抵抗）に収束することが見て取れます。

\[ \lim_{V_c \to 0} \ Zi = \frac{V_T}{I_s} \tag{7} \]

すなわち、入力が熱電圧 $V_T$ (26mVぐらい)よりも小さいと、ダイオードは普通の抵抗器のような振る舞いを見せるということです。その抵抗値が $V_T / I_s$ になります。

そして、大信号を入力したときは、先ほどの式(2)と全く同じ形に帰着します。

\[ Z_i = \frac{R_o}{2\eta} \tag{2} \]

なので、ある一定以上の信号入力があるならば、式(2)でも十分でしょう。当然ながら、大信号の極限ではRo/2に漸近します。

上記の式についての導出過程や性質を知りたい方は、こちらの補足資料No.2をご覧ください。

計算シミュレーション

では、それぞれの式を実際に計算してみます。下記のグラフはIs=1μA、負荷抵抗Ro=100kΩの場合（凄く代表的な値）の数値計算結果です。

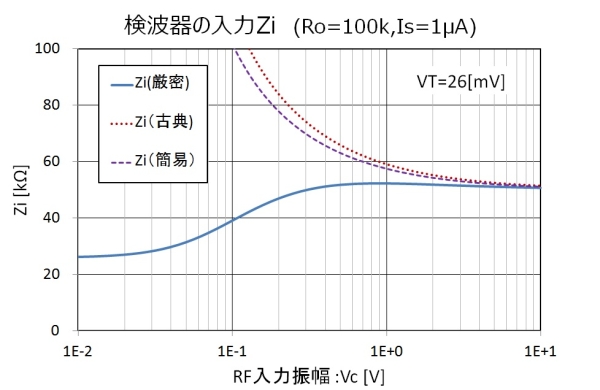
図５.入力Ｚ（100kΩ 1μA）

この場合、かなり厳密式と古典式の相違が大きくなりました。傾向としてはダイオードの感度が良い＝Isが大きいほど、古典式との違いが大きくなるようです。

また、このような条件だと、小入力になるほど逆にインピーダンスが下がってしまい、感度低下の原因となる可能性があります。

では、感度が悪いと言い切るには惜しいが、もう一声！というIs=0.1μA、負荷抵抗Ro=100kΩの場合をグラフに描いてみます。

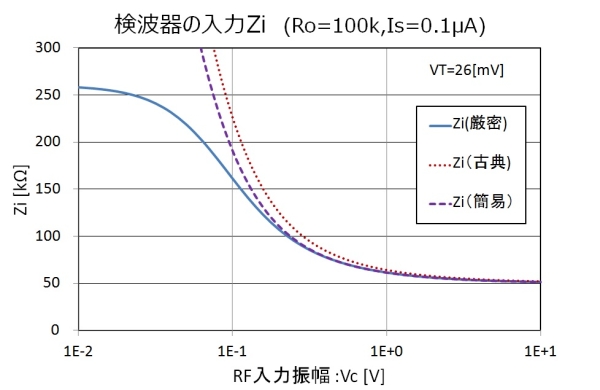
図６.入力Ｚ（100kΩ 0.1μA）

この場合ですと、古典式も厳密式も極端な違いは見えません。つまり、条件によって古典式を当てはめてよい場合とそうでない場合があるという事です。

最後に、Ro=100kΩ,10kΩ,Is=1μA,0.1μAの4通りで計算した厳密解によるグラフを紹介します。

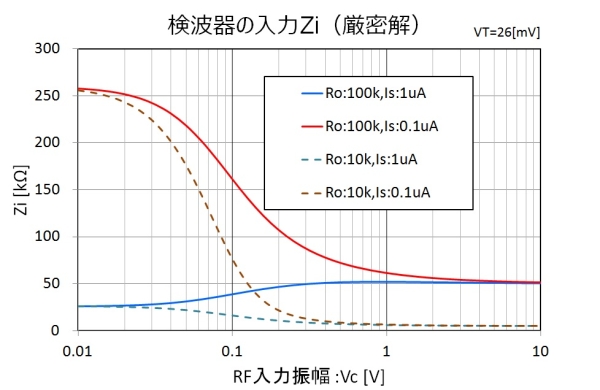
図７.入力Ｚ（厳密解）

実測の例

入力インピーダンスを実測した例を紹介します。ダイオードは松下製のＭＡ７００（シリコンショットキー）を使用し、同調回路への入力電圧を一定に保ったまま、負荷抵抗を変化させ、そのＱの低下具合から間接的に入力Ｚを測定した結果です。

抵抗値は22kΩ～3.3MΩまで変化させました。22kΩのときのDC出力が0.3V、同じく3.3MΩ時のDC出力電圧は3.0V程度です。（Ro/2に近い値）

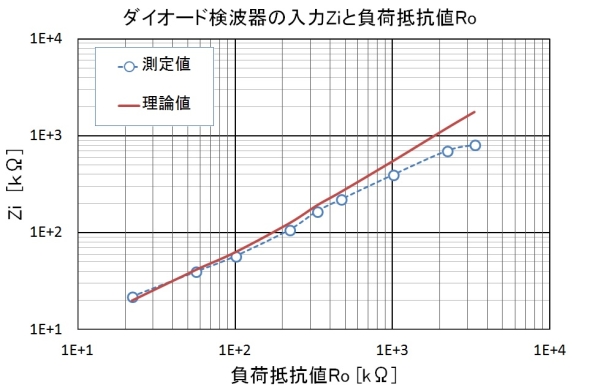
図８.入力Ｚの測定例

結果としては、ほぼ理論に近い値が出ています。一般的なRo=100kΩの時には、理論値63kΩに対して実測Zi=58kΩとよい一致が見られました。

ただし、負荷抵抗値が大きくなるほど入力Ｚが低下傾向にあります。3.3MΩのRoを使用しても,Zi=814kΩと理論値の1.76MΩに届いていません。

軽い負荷での入力Ｚ低下原因は、ダイオードの並列寄生抵抗成分のようです。ダイオードによって異なりますが、実測すると数百kΩから十数MΩ程度の値をとる非線形抵抗成分です。幾つかダイオードを取り替えて試してみると、1SS108のような「高感度で逆抵抗（オーム性）が小さい」ものほど、入力Ｚの低下が顕著なことが見えてきたところです。

特に興味のある部分は、感度に大きくかかわる微小入力時ですから、今後はこの領域のZiを正確に測定することが課題となりそうです。（結構難しい…）

簡単なまとめ

検波器の入力Ｚは、負荷抵抗Roの選択でほぼ決定される。
ただし、入力信号レベルにも影響を受ける。
0.5V～1V以上の大信号なら、Zi=Ro/2に収束する。
100mV以下の微小信号では、ダイオード特性(Is)が大きく影響。
高感度なダイオードほど、微小信号での入力Ｚが低下する。
微小信号の極限では、Zi=VT/Isに収束。