（付録１）
検波器の入力インピーダンス

本ページは検波器の入力インピーダンスの補足資料です。 \[ Z_i = R_o \ \frac{\tan \theta -\theta}{\theta - \sin \theta \cos \theta} \] なる古典式の導出過程について問い合わせがあったため作成したものです。また、この式が近似的に \[ Z_i = \frac{R_o}{2 \cos \theta} \] になることも併せて紹介します。

本式は、ダイオード特性を線形近似した包絡線検波回路の回路解析結果で、数十mV 以下の微小信号では誤差が大きくなるものの、数百mV以上の大信号では挙動がよく一致する特徴があります。

単純な、図１の回路を対象とします。

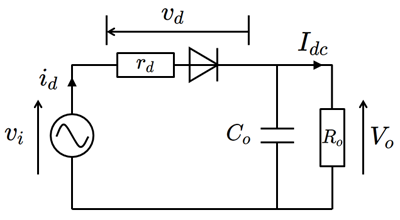
fig.1 解析対象の回路モデル

前提として、静電容量 $C_o$ は十分に大きく、入力周波数に対して短絡とみなせる仮定をします。またダイオード特性は、内部抵抗成分を考慮して線形近似した 式(1) に従うとします。 \begin{eqnarray} i_d = \left \{ \begin{array}{ll} \cfrac{v_d}{r_d} & (v_d \geq 0) \\ 0 & (v_d \lt 0) \\ \end{array} \right. \tag{1} \end{eqnarray}

ここで、各記号は以下の通りです

$i_d$

ダイオード電流[A]

$v_d$

ダイオードの両端電圧[V]

$r_d$

ダイオードの内部抵抗（順抵抗）[Ω]

式(1)の特性をグラフで描けば図２のようになります。

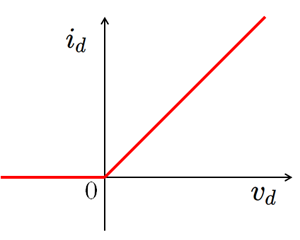
fig.2 仮定するダイオードの電圧電流特性

言い換えれば、負電圧では電流ゼロ、正電圧ではダイオードの内部抵抗に応じた電流が流れるという直線的なモデルになります。

簡単のため、入力RF電圧 $v_i$ を、振幅 $V_c$ の正弦波とすれば、 \[ v_i= V_c \cos \theta \tag{3} \] と表現できます。このときの波形の概形は図３のようになります。

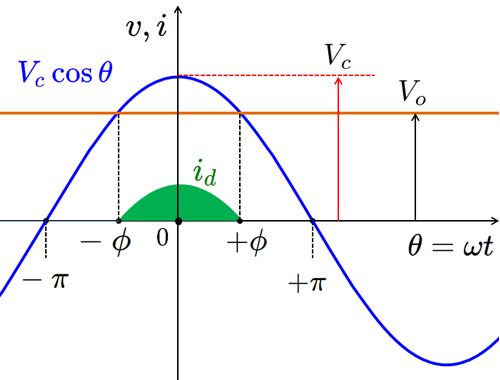
fig.3 波形の概要

正弦波の振幅が出力DC電圧 $V_o$ を超えた時だけ、ダイオードに電流 $i_d$ が流れることになるのですが、その流れ始めと終わりの位相を $\pm \phi$ とします。（専門的には導通角や流通角と呼ばれる値です。）

そのタイミングでのダイオード両端電圧 $v_d$ は、入力電圧 $v_i$ と出力DC電圧 $V_o$ との差になるので、 \[ v_d = v_i - V_o = V_c \cos \theta - V_o \tag{4} \] その一方で、出力DC電圧は図3より \[ V_o = V_c \cos \phi \tag{5} \] の関係が成立していることを考慮すると、式(1)は最終的に、 \[ i_d = \frac{V_c}{r_d} \left( \cos \theta - \cos \phi \right) \tag{6} \] と書き換えることができます。（ただし、 $-\phi \leq \theta \leq +\phi $ の位相の間に限ります。）

式(4) を式(1)に代入し、交流一周期の平均を取ると、ダイオードに流れる直流電流成分 $I_{dc}$ が求められます。式で表せば \[ I_{dc} = \frac{1}{2\pi} \int^{\pi}_{-\pi} i_d \ d\theta \tag{7} \] が定義です。

このダイオード電流 $i_d$ は$\theta = 0$ の軸に対して対称（偶関数）になっており、全体を２倍にして積分区間をπ～0と半分にできることに気付きます。また、その積分区間もダイオードがオンになるφ～0だけに絞ればよいです。まとめて、式(7)を \[ I_{dc} = \frac{1}{\pi} \int^{\phi}_{0} i_d \ d\theta \tag{8} \] として、計算しやすくしておきます。

式 (8) に式 (6) を代入して実際に積分すると、 \begin{eqnarray} I_{dc} &=& \frac{1}{\pi} \int^{\phi}_{0} \frac{V_c}{r_d} \left( \cos \theta - \cos \phi \right) \ d\theta \\ &=& \frac{V_c}{\pi r_d} \int^{\phi}_{0} \cos \theta - \cos \phi \ d\theta \\ &=& \frac{V_c}{\pi r_d} \Bigl[ \sin \theta -\theta \cos \phi \Bigr]^{\phi}_{0} \\ &=& \frac{V_c}{\pi r_d} \left( \sin \phi -\phi \cos \phi \right) \tag{9} \end{eqnarray}

式（9）に出力抵抗 $R_o$ をかければ出力DC電圧 $V_o$ になるので、 \[ V_o = \frac{V_c R_o}{\pi r_d} \left( \sin \phi -\phi \cos \phi \right) \tag{10} \]

この式(10)と式(5)は共に、出力DC電圧 $V_o$ であるので、 \[ V_o = \frac{V_c R_o}{\pi r_d} \left( \sin \phi -\phi \cos \phi \right) = V_c \cos \phi \tag{11} \] が成立しますから、 \[ \frac{\pi r_d}{R_o} = \tan \phi-\phi \tag{12} \] の関係があり、後でこの式(12)を利用することになります。

入力インピーダンス $Z_i$ を求めるには、先に入力電力 $P_{in}$ を求めておく必要があります。ここで入力電力は入力周波数における電圧と電流の積から計算でき、 \begin{eqnarray} P_{in} &=& \frac{1}{2\pi} \int^{\pi}_{-\pi} i_d \ V_c \cos \theta \ d\theta \\ &=& \frac{1}{\pi} \int^{\phi}_{0} \frac{V_c}{r_d} \left( \cos \theta - \cos \phi \right) \ V_c \cos \theta \ d\theta \\ &=& \frac{V_c^2}{\pi r_d} \int^{\phi}_{0} \left( \cos \theta - \cos \phi \right) \cos \theta \ d\theta \\ &=& \frac{V_c^2}{\pi r_d} \left( \frac{1}{4} \sin 2\phi + \frac{\phi}{2} - \sin \phi \cos \phi \right)\\ &=& \frac{V_c^2}{2 \pi r_d} \left( \phi - \sin \phi \cos \phi \right) \end{eqnarray} よって、入力から見た検波器の消費電力 $P_{in}$ は \[ P_{in} = \frac{V_c^2}{2 \pi r_d} \left( \phi - \sin \phi \cos \phi \right) \tag{13} \]

入力インピーダンス $Z_i$ は、 \[ Z_i = \frac{V_c^2}{2 P_{in}} \tag{14} \] が定義なので、これに式(13)を代入して \[ Z_i = \frac{\pi r_d}{\phi - \sin \phi \cos \phi} \tag{15} \] が得られます。

ここで、式(12)を利用して $\pi r_d$ の項を $\phi$ の関数と $R_o$ で置き換えると \[ Z_i = R_o \frac{\tan \phi -\phi}{\phi - \sin \phi \cos \phi} \tag{16} \]

この 式(16) が、本ページで求めたかった古典的な検波回路の入力インピーダンス式になります。

$\phi = 0$ （検波効率が100%）のとき、式(16)に $\phi = 0$ を代入しても 0/0 の不定形になってしまうので簡単には値が求まりません。これは、ダイオードに電流が流れるタイミングが無いという意味になるからです。そこで、極限値を得るために分母と分子をそれぞれ微分して極限を取ることにすれば、 \begin{eqnarray} \frac{(\tan \phi -\phi)'}{(\phi - \sin \phi \cos \phi)'} &=& \frac{\sec^2 \phi-1}{1-\cos 2\phi} \\ &=& \frac{1-\cos^2 \phi}{\cos^2\phi(1-\cos 2\phi)} \\ &=& \frac{\sin^2 \phi}{\cos^2\phi\cdot 2 \sin^2 \phi} \\ &=& \frac{1}{2 \cos^2 \phi} \end{eqnarray} と計算できるので、最終的に、 \[ \lim_{\phi \rightarrow 0} Z_i = \frac{R_o}{2} \tag{17} \] の結果が得られます。これは入出力のパワーが等しいと仮定した時の単純解に一致します。

それとは逆に、$\phi = \pi/2$ （検波効率がゼロ）のときは、 \[ \lim_{\phi \rightarrow \pi/2} Z_i = \infty \tag{18} \] と、無限大に発散します。つまり消費電力がゼロという意味になります。古典式の精度が悪い領域はこのあたりです。

それらの中間にあたる流通角では、 \begin{eqnarray} \frac{\tan \phi -\phi}{\phi-\sin \phi \cos \phi} &=& \frac{1}{\cos \phi} \cdot \frac{\sin \phi - \phi \cos \phi }{\phi-\sin \phi \cos \phi} \\ &\approx & \frac{1}{2 \cos \phi} \\ \end{eqnarray} と、大まかに近似することができるので、入力インピーダンスは \[ Z_i = \frac{R_o}{2 \cos \phi} \tag{19-1} \] と表せるのですが、$ \cos \phi $ は電圧検波効率 $\eta$ の定義に等しいことから、 \[ Z_i = \frac{R_o}{2 \eta} \tag{19-2} \] と、書かれる事が多いです。

\[ \frac{\sin \phi - \phi \cos \phi }{\phi-\sin \phi \cos \phi} \approx \frac{1}{2} \tag{20} \] の項ですが、入り組んでて分かりにくい関数だったので、ちょっと補足しておきます。

単純に $\phi=0$ を代入すると、結局これも 0/0 になって極限を工夫してとらなくてはなりませんが、先ほどと同じように分母・分子を微分した上で極限をとればよく、 \begin{eqnarray} \frac{(\sin \phi - \phi \cos \phi)'}{(\phi-\sin \phi \cos \phi)'} &=& \frac{\cos \phi -\cos \phi + \phi \sin \phi}{2 \sin^2 \phi} \\ &=& \frac{\phi}{2 \sin \phi} \\ &=& \frac{1}{2} \cdot \frac{\phi}{\sin \phi} \end{eqnarray} と計算したうえで、 \[ \lim_{x \rightarrow 0} \frac{\sin x}{x} =1 \] の sinc関数 の極限としてよく知られた結果を利用すると、 \[ \lim_{\phi \rightarrow 0} \frac{1}{2} \cdot \frac{\phi}{\sin \phi} = \frac{1}{2} \] なります。

次に、 $\phi = \pi/2$ の値を求めれば、 \[ \frac{1}{\pi/2} = \frac{2}{\pi} = 0.6366 \cdots \] です。

結局、 式(20) の関数は $\phi$ が 0 から 90° まで動いたところで、 0.5 から 0.637 までしか身動きせず、しかも単調関数なので、ほぼ 0.5 と割り切ってしまったのが、 式(19-1) ということです。