包絡線検波器(ダイオード検波器)の理論解析2
(前ページ)に戻る
ダイオードの電圧降下影響
前ページでの解析は、無負荷の検波器を中心としたものでしたが、実際には、負荷を付けなければエネルギを取り出すことはできません。図1のように抵抗Rが無くてはならない訳ですが、抵抗器として目に見える部品が存在するだけでなく、イヤホンなどの負荷が抵抗Rの役割を果たしている事も多々あります。
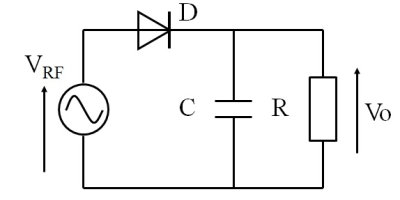
図1.ダイオード検波器(包絡線検波器)
それで、実際に抵抗をつけると出力電圧が下がるのですが、その下がり方を求めるのは非常に難しいということを、前ページで紹介しました。しかも、ゲルマ/鉱石ラジオの感度は、ほぼここの部分で決まります。
その難しさの原因は、ダイオードの非線形特性にあります。単純には図2の回路を解析できればいいのですが、電子回路初学者を惑わすには格好の「簡単な回路」です。
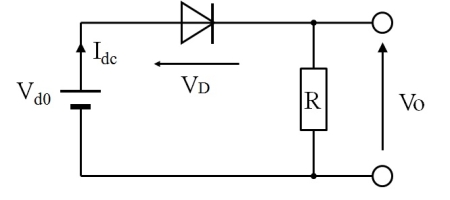
図2.ダイオード検波器の直流等価回路
図2の出力電圧を求めるには、以下の式を解く必要がありますが、手計算でお手軽に解くことは無理な相談なのです。(出来ないわけではないが、かなり面倒)
\[ V_{d0} - V_T \ln \left( 1 + \frac{V_o}{I_s R} \right) -V_o =0 \tag{1} \]では、いきなり数値シミュレーションした結果を紹介します。図3はダイオードが持つ逆方向飽和電流$I_s$によって、どのように出力が変化するかを表したものです。
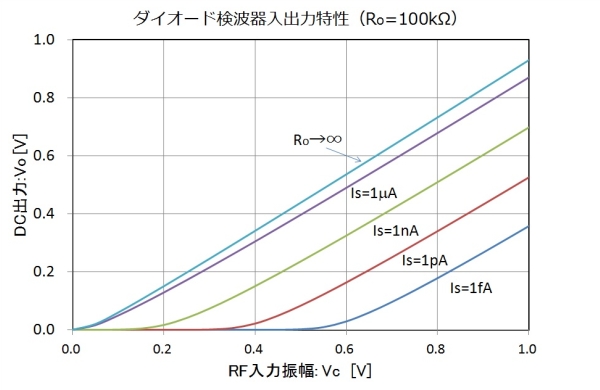
図3.100kΩ負荷時の検波器出力(各Isの比較)
出力抵抗Roは、一般的な100kΩを仮定しました。$I_s$が1fA~1pAというのは、シリコンダイオードの範疇です。また、$I_s$が1nA~1μAは、鉱石/ゲルマ/シリコンショットキーバリアダイオードの範疇です。
定性的に述べれば、$I_s$が大きいダイオードほど大きな出力が得られることがわかります。
これは単純な話で、ダイオードの立ち上がり電圧に大きく影響を受けると言い換えることができます。
図4は、ダイオード電流が1mAまでの範囲で、$I_s$ごとの電圧―電流特性を描いたものです。これを見れば一目瞭然ですが、$I_s$が大きいダイオードほど小さい電圧で電流が流れ始めます。
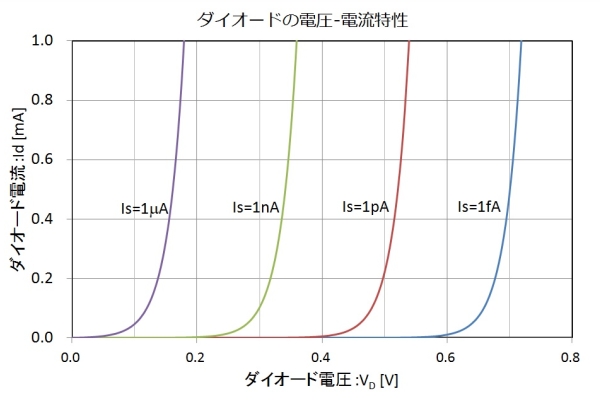
図4.ダイオードのV-I特性
電子回路設計の一般的な設計では、ダイオードが0.7V程度でONになると仮定したり、あるいはトランジスタのベース・エミッタ間電圧を0.6Vとおいて設計を始めます。よく使用する電流領域では、式(1)の方程式を解くこと無く概算値で代用してしまえることが要因です。
もともと、$I_s$は温度に影響されたり、素子のバラつき範囲が1桁を軽く超えたりと、あまり一定しないことから、精密に求める機会は少ないでしょう。また、回路設計上もこのバラツキに影響されないようにします。
では、実際に影響が出るパラメータを絞り込みましょう。$I_s$が大きいダイオードを使用できたとしても、出力抵抗Rが小さければ電流がたくさん流れてしまい、出力電圧$V_o$はかなり低下してしまいます。
つまり、この電圧降下を決定する量は、$I_s \times R_o$の値と考えるのが妥当でしょう。$I_s$と$R_o$が変化しても、その積が一定であれば、出力電圧$V_o$は変化しません。
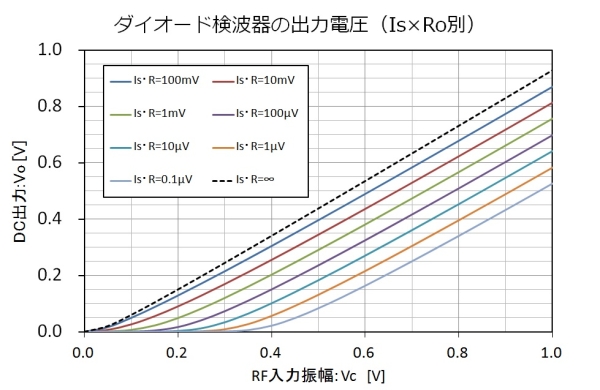
図5.$I_s$・Ro別の検波器出力特性
図5は、$R_o = 100 \mathrm{[k\Omega]},I_s=0.1 \mathrm{[\mu A]}$(=10mV)の時と、$R_o = 10 \mathrm{[k\Omega]},I_s=1 \mathrm{[\mu A]}$ (=10mV)では、同じ出力電圧である…という事を示しています。直線検波領域では、$I_s \times R_o$が一桁変化すると、50mV~57mV程度の出力変化があり、その差はそれほど変化していません。
ダイオードが本来もっている特性(10倍電流を増やすごとに、端子電圧が59mVずつ上昇していく特性)が強く影響するからでしょう。
ただし、出力電圧$V_o$は同一でも、出力パワー$P_{out}$は異なりますので注意してください。上の例では、$P_{out}=V_o^2/R_o$から、10kΩの負荷抵抗の方が出力電力が10倍大きくなる計算です。
誤解を招くと困るので、さらに注意点を追加しておきます。負荷$R_o$が100kΩと10kΩとでは、検波器の入力インピーダンスも10倍ほど違い、実回路では100kΩの方が出力パワーが大きいという場合もありえます。
このような問題が生じるのは、図1の回路に理想電圧源という無尽蔵なパワーをもつ高周波電源を仮定しているからです。実際には、非常に高いインピーダンスの電源=同調回路で動作するのがゲルマ/鉱石ラジオですので、この解析結果を単純に当てはめることはできません。あしからず。