（付録３）
検波器の入出力電圧式の導出

本ページは、包絡線検波器（ダイオード検波器）の理論解析の付録です。

理論式の導出過程

単純な、fig.1の回路を考えます。

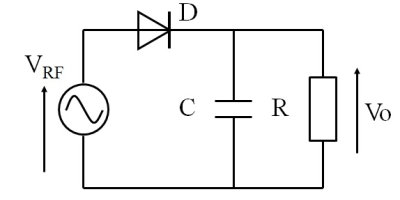
ダイオード検波器の回路モデル

fig.1 ダイオード検波器の回路モデル

ダイオード特性は、一般的なダイオード電流式 (1) に従うとします。

\[ i_d = I_s \left(e^{v_d/V_T}-1 \right) \tag{1} \]

ここで、ここで、各記号は以下の通りです

$i_d$
ダイオード電流[A]
$I_s$
ダイオードの逆方向飽和電流[A]
$v_d$
ダイオードの両端電圧[V]
$V_T$
ダイオードの熱電圧[V]

$V_T$ は、熱に関係する定数で、式(2)で定義されます。$k$ はボルツマン定数、 $T$ は絶対温度、$q$ は電荷素量で、室温では 26mV 程度が標準値ですが、放出係数あるいは理想係数と呼ばれる $n$ が1～2の値であるため、等価的に 26mV ～ 52mV 程度の値となります。

\[ V_T = n \frac{kT}{q} \simeq n \times 26 \mathrm{[mV]} \ \ , (T=300K) \tag{2} \]

もっとも、定数のふりをしている $I_s$ は温度に大きく影響されますのでご注意。以下は、静特性の測定結果の一例です。半導体は品番が同じでも全く同一の特性が出ることはまず無いですし、温度や測定条件に大きく左右されますので、あくまで参考に過ぎません。

表１．各種ダイオードの静特性の例（個人測定）
ダイオード種別 Is VT 測定条件 Condition
1N60 1.04μA 29.9mV 0.1 ≤ Id ≤ 330μA
2SA50 0.821μA 25.4mV 0.1 ≤ Id ≤ 1.5mA
1SS108 3.55μA 27.1mV 18μ ≤ Id ≤ 4.5mA
1S2076 10.0fA 28.0mV 0.1μ ≤ Id ≤ 4mA
SB0030-4A 8.43nA 25.9mV 0.4μ ≤ Id ≤ 4.5mA

また、fig.1 の回路の負荷キャパシタ C は、入力RF周波数に対して完全に短絡状態であると仮定します。

まずは簡単のために入力RF電圧 $v_i$ を振幅 $V_c$ の正弦波とすると。

\[ v_i= V_c \cos \theta \tag{3} \]

すると、ダイオードの両端電圧 $v_d$ は出力DC電圧 $V_o$ と入力RF電圧$v_i$ の差となるので、

\[ v_d = V_c \cos \theta - V_o \tag{4} \]

式(4)を式(1)に代入し、交流一周期の平均を取ると、ダイオードに流れる直流電流成分 $I_{dc}$ が求められます。式で表せば \[ I_{dc} = \frac{1}{2\pi} \int^{\pi}_{-\pi} i_d \ d\theta \tag{5} \] であって、その時のダイオード電流 $i_d$ は、 \[ i_d = I_s \left[ \exp \left(\frac{V_c \cos \theta -V_o}{V_T}\right) -1\right] \tag{6} \] となります。

式(5)に式(6)を代入して実際に積分すると、

\begin{eqnarray} I_{dc} &=& \frac{Is}{2\pi} \int^{\pi}_{-\pi} e^{\frac{V_c \cos \theta -V_o}{V_T}} d\theta -\frac{I_s}{2\pi} \int^{\pi}_{-\pi} d\theta \\ &=& I_s \ e^{-\frac{V_o}{V_T}} \frac{1}{2\pi} \int^{\pi}_{-\pi}e^{\frac{V_c}{V_T}\cos \theta } d\theta -I_s \\ &=& I_s \ e^{-\frac{V_o}{V_T}} \left[ \frac{1}{\pi} \int^{\pi}_{0} e^{\frac{V_c}{V_T} \cos \theta } d\theta \right] -I_s \\ &=& I_s \ e^{-\frac{V_o}{V_T}} \ f_0(x) -I_s \ \ , \ \ (x=V_c/V_T) \\ &=& I_s \left( e^{-\frac{V_o}{V_T}} \ \ f_0(x) -1 \right) \tag{7} \end{eqnarray}

途中、コサインを含む積分式を、第1種0次変形ベッセル関数に置き換えています。 通常は、この関数を $I_0(x)$ と表記するのですが、電流の $ I $ 記号と紛らわしいため、いったん $f_0 (x)$ としました。

０次ベッセル関数 $J_0(x)$ と0次変形ベッセル関数 の関係、及びその積分表示と級数展開は以下のとおりです。

\begin{eqnarray} J_0 (jx) = f_0 (x) &=& \frac{1}{\pi} \int_{0}^{\pi} e^{x \cos \theta} d \theta \\ &=& \sum_{k=0}^{\infty} \frac{(x^2/4)^{k}}{(k!)^2} \tag{8} \end{eqnarray}

式(7)で、ようやくDC電流値が求められたのですが、出力電圧 $V_o$ を求めていきたいため、 $V_o$ を中心に変形して両辺を自然対数化し整理します。

\begin{eqnarray} \ln \left[ \frac{I_{dc}}{I_s} + 1 \right] &=& \ln \left[ e^{-\frac{V_o}{V_T}} \ f_0(x) \right] \\ \\ &=& -\frac{V_o}{V_T} + \ln [ f_0(x)] \tag{9} \end{eqnarray}

最終的に、これを $V_o$ について解くと、検波回路の出力電圧が式(10)の形で得られます。

\begin{eqnarray} V_o &=& V_T \ln \left[f_0\left(\frac{V_c}{V_T}\right) \right] - V_T \ln \left[1 + \frac{I_{dc}}{I_s} \right] \tag{10} \end{eqnarray}

なお、この式(10)右辺にある $I_{dc}$ は出力電圧 $V_o$ の関数です。なぜなら、ごく普通の検波器では負荷抵抗 $R$ に流れる電流 $I_{dc} $ が $V_o/R$ に固定されるからです。そのため、fig.1 のモデルでは、$V_o$ 基準にした表現に書き直すこともできます。

\[ V_o = V_T \ln \left[f_0\left(\frac{V_c}{V_T}\right) \right] - V_T \ln \left[ 1 + \frac{V_o}{R_o I_s} \right] \tag{11} \]

ここで、式(10),(11)の第1項がほぼ入力振幅 $V_c$ で決まる検波起電力、第2項がダイオードの直流電圧降下を意味します。熱電圧 $V_T$ は、どのダイオードでも極端な変化はないはずなので、ダイオードの違いによる検波出力の大小（＝感度）は、逆方向飽和電流 $I_s$ に大きく依存することになります。

式(10)又は(11)は、非線形方程式であるため、シミュレーションぐらいしか解く方法がありません。ダイオード検波器の難しさはここに起因しているのだと思います。

特に、興味深いのは、出力電圧 $V_o$ あるいはDC電流値 $I_{dc}$ に任意性があることです。本ページでは、抵抗 $R_o$ のみがそれらを決める条件と仮定した導出をしているのですが、２次側に信号を印加する条件も適用できたりします。

要するに、１次側の入力が２次側に出力されるだけでなく、逆の経路もあるということ。もっとベタな言い方ならば、ダイオード検波器は変調器としても動作するという表現になるでしょう。

放送受信中のゲルマラジオの同調回路近傍に一般的なＡＭラジオを置くと、イヤホンへ入った音がＡＭラジオを通して聞こえてくるのは、このような仕組みによるものです。

本式のより定性的な説明は、包絡線検波器の理論解析１を参照してください。