ダイアゴナルクリッピング歪って何?
1.ダイオード検波器の歪
ダイオード検波器(Diode Detector)あるいは、包絡線検波回路(Envelope Detector)には、どうしても発生してしまう歪があります。
発生する歪の種類は、以下のものが代表的です。
- 非直線歪(2乗検波歪)
- ダイアゴナル・クリッピング歪(Diagonal Clipping)
- ネガティブ・ピーク・クリッピング歪(Negative Peak Clipping)
上の3種類のうち、「ダイアゴナルクリッピング」はやたらと検索語に多いのでこのようなページを作ってみました(学生さんかな?)。Web上には確かに解説しているのが少ないんですね。
本来、検波器というのはダイオードによって作られた「歪み」のおかげで検波できるのですが、その復調信号に歪が多くてはならず、何だか矛盾した存在だなぁと思う時もあります。
2.非直線歪み
別名、2乗検波歪と言いまして、ゲルマ/鉱石ラジオでは、必ず経験する復調歪です。
普通のラジオでも経験することで、車でAMラジオを聴きながらトンネルの入り口に差し掛かるとき、あるいは放送エリアギリギリの場所でよく発生します。
どのAMラジオでも感度が限界に達するあたりで、この非直線歪が発生します。(高級機だと同期検波器が搭載されているので、例外もあり。)
単純には、検波器の入出力関係が直線的でないことが要因。より具体的に言えば、ダイオード検波器が微弱信号に対して2乗特性を持つことが最大の原因です。
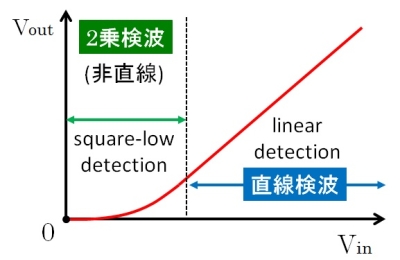
図1.検波器の特性曲線
歪が増えるのは、おおむね0.2~0.3V以下の入力。20~30mV以下だと、ほぼ完全に2乗特性になります。
この辺りの信号相手に奮闘するゲルマ/鉱石ラジオだと、かなりの確率で2乗歪に見舞われるわけですね。その代わりと言っては何ですが、直線検波と比べて2倍の復調出力を得られるメリットもあります。
高周波パワーメータだと、電力に比例した出力が得られる2乗特性が好まれていたりしますが、音声・楽音を忠実に再現するには直線特性でなければいけません。
図2は分かりやすいように、三角波の変調波を入力したときの出力を描いたものです。2乗特性によって出力が歪む様子がわかると思います。
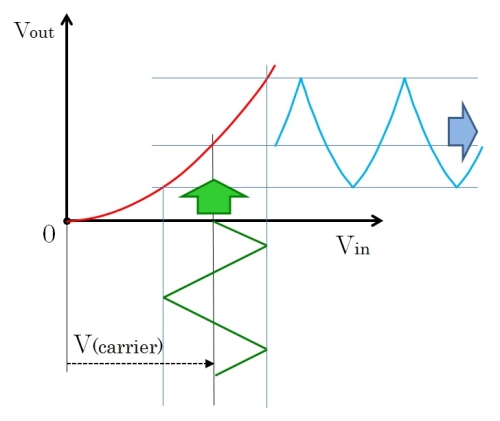
図2.非直線歪の例
この非直線歪、AM変調度と密接な関わりがあり、変調度が大きい場合、すなわち音声信号が大きいほど歪がひどくなります。変調度100%の場合には25%もの歪み率(THD: Total Harmonic Distortion )に達します。
\[ \mathrm{THD} = \frac{m}{4} \tag{1} \]式(1)は、2乗検波において、純音(sin波)を1つだけ変調した場合に導かれる式です。(音声のような複雑な波形だと歪みも複雑になりますので、さらに悪化しそうですが、どうなのかな?)
図3は、実際に変調度を最大の1(100%)にしたときの三角波の復調波形です。図2に比べてかなり歪み度合いが増えているように見えるでしょう。
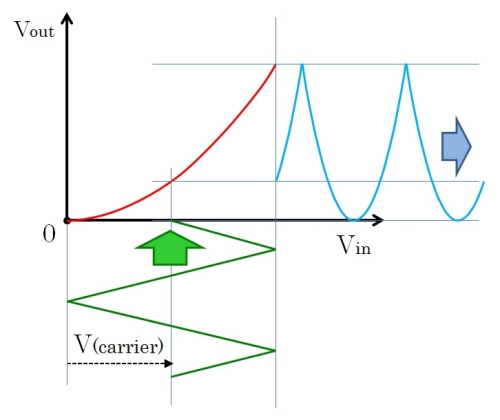
図3.非直線歪の例2
これらの非直線歪みは、ゲルマ/鉱石ラジオにおいて発生が不可避であり、本質的な改善が困難です。強い入力を確保し、同調回路のQを上げ、損失を最小限に抑えるなどの、2次的な対策ぐらいしか方法は無さそうです。
3.ダイアゴナルクリッピング歪み
別名、袈裟切りひずみ、斜めクリッピング歪みと呼ばれる歪みです。袈裟切りっていう和名は物騒な名前だなぁ。
これは、検波回路が信号に追従できない事によって生じる歪みで、出力に付いているキャパシタCと抵抗Rの不適切な値によって引き起こされるもの。特に高感度を狙うほど歪が出やすくなります。
分かりやすいのは、矩形波(方形波)の変調信号を入力した図4のような場合で、入力RF信号が時刻T秒で消えたにもかかわらず、しばらく尻尾を引いてしまいます。
この尻尾が斜めの直線に見える場合がほとんどであることから、ダイアゴナル(斜め)クリッピング(切り取り)波形歪みと呼んでいます。
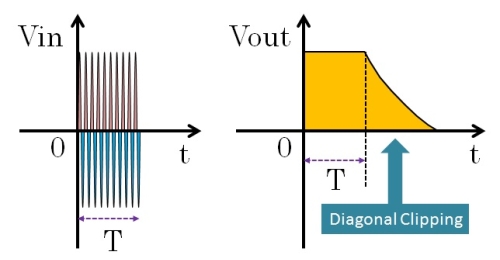
図4.ダイアゴナルクリッピング
では、なぜこのような事が生じるのでしょうか?。そこで、ダイオードが無い包絡線検波回路の挙動を考えます。図5は、単純なCR並列回路で、SWをON/OFFした時にどのような挙動となるか見てみましょう。
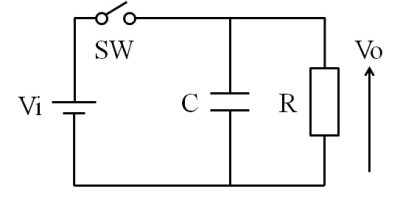
図5.CR並列回路のステップ応答
図5で、SWをONとしたときの出力電圧波形は、下記の図6のようになります。
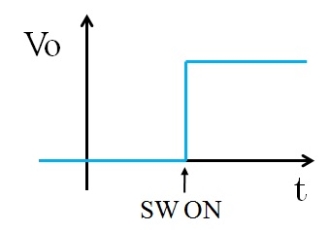
図6.SWオン時の波形
SWを投入した直後、瞬時にキャパシタCが充電されて、出力電圧Voは入力電圧Viと等しくなります。この間、理論上の立ち上がり時間はゼロです。
そして、ここでSWをONにしたまま、電源電圧Viを自在に変えてみることにします。
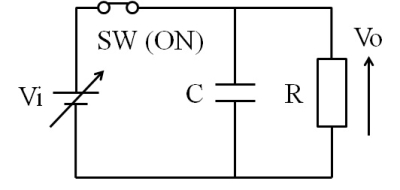
図7.SWオン状態のCR回路
すると、出力電圧Voは、見事に電源電圧Viの変化に追従してきます。どんなに急峻であろうが、緩やかであろうが、図8のようにピッタリくっ付いてきます。
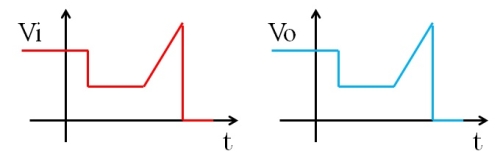
図8.SWオン時の電源電圧と出力電圧波形
つまり、スイッチがONされている限り、出力電圧は常に入力電圧と等しくなるという回路の性質があるわけです。あまりにもツマラナイので過渡現象の教科書では無視されることも。
しかし、SWをOFFにして回路を切り離すと事情が変わってきます。図9は、SWをOFFにした直後の出力電圧波形です。
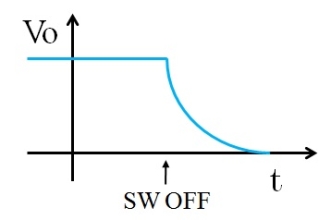
図8.SWオフ時の出力電圧波形
SWをオフにすると、キャパシタCと抵抗Rのみの回路となり、Cに充電された電荷Qが行き場を失って全てRに流れます。そして、電荷が尽きるまでそれは続きます。
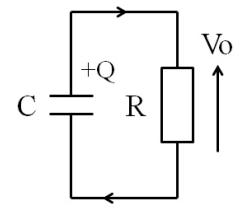
図9.SWオフ時の回路と電流の流れ
このSWと同等の動作をするのがダイオード。入力電圧が急に小さくなるときのみ、ダイオードがOFF状態になり、CとRの回路が入力と切り離されてしまいます。キャパシタCに充電された電圧Voが、入力電圧Viよりも大きくなってしまうからですね。
ダイオードは一方向にしか電流を流さないという、単純な事実です。
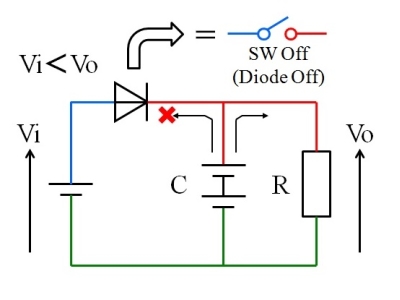
図10.ダイオードのオフ状態発生
その結果、図11のように、入力の「減少方向」への変化に対応しきれず、だらだらと斜めに切ったような波形となるのです。これがダイアゴナルクリッピングの発生要因です。
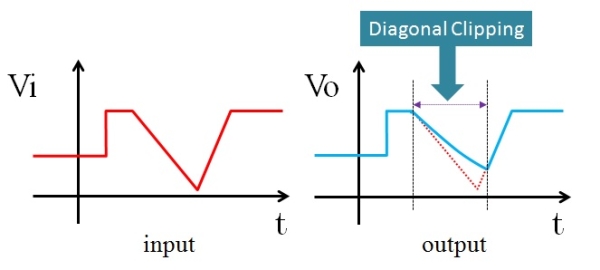
図11.ダイアゴナルクリッピングの発生
この減少時間は、CとRによって決まる時定数Tに関係してきます。 \[ T=CR \tag{1} \]
例えば、C=100pF、R=100kΩとすると、時定数Tは10μs。端的に言えば、急に入力がゼロになったとき、10μsごとに37%づつ出力電圧が減少(放電)していくことを表しています。無視できる電圧が5%程度と考えると、そこに到達するまで39μs、1%なら46μs程度の時間が必要です。
非常に短い時間なので、大した影響がないと感じますが、高い周波数の復調信号に対しては厳しくなってきます。図12は10kHzの復調信号と、時定数(10μs)による影響を比較してみたものです。
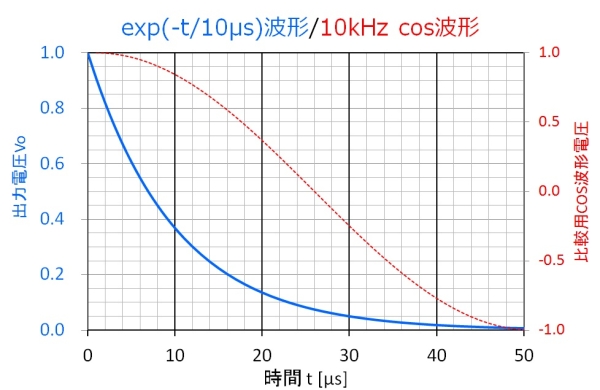
図12.時定数(10μs)と正弦波(10kHz)の比較
う~ん、10kHzぐらいなら何とかなりそうかな?という印象。でも、これがC=1000pF、R=100kΩで10倍の時定数T=100μsならどうでしょうか?
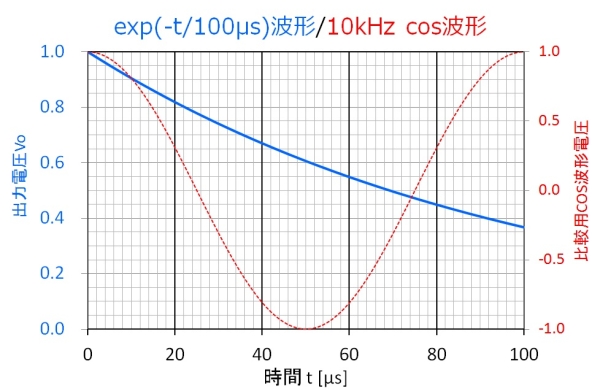
図13.時定数(100μs)と正弦波(10kHz)の比較
完全に出力が追いつかないようです。波形も斜めに切り取られる事は確実です。
要するに、ダイアゴナルクリッピング歪みは、高抵抗のR、大容量のCを使ったときに高い周波数信号成分に対して発生する歪みです。(注:歪んだ結果として低い周波数成分も含まれます。)
検波効率を上げるには、Rをなるべく大きくする必要があります。また、Cもある程度以上の容量でなければ、効率が下がってしまいます。つまり時定数を大きくするほど感度が上昇するのですが、大きくしすぎるとラジオとして役立たずになってしまうのです。
では、どの程度の時定数に留めておくべきなのか?一つの目安が、以下の式です。 \[ \frac{1}{CR} \geq 9.21 \cdot f_{max} \cdot \log_{10} \left( \frac{1}{1-m} \right) \tag{2} \]
ここで、$f_{max}$は復調信号の最高周波数、$m$はAM変調度$(0 \leq m \lt 1)$です。
AM放送の平均変調度mは0.3程度と言われますが、音声や音楽のピーク値を考慮すると、0.8とか0.9などのキツめの変調度を仮定した方がよさそうです。また、最高信号周波数fmは、実際のAM放送スペクトルを考慮すると10kHzあれば十分でしょう。ここは割り切って3kHz程度としてしまう場合もあります。が、それにしても余裕が無さ過ぎなので、せめて5kHzぐらいを狙いたい所。
それらの条件で算出してみましょう。m=0.8、fm=10kHzとすると、CRは15.5μs以下であることが推奨条件となります。感度・選択度を考慮してR=100kΩとすると、キャパシタCは155pF以下であることが要求されます。
ですので、100pF~150pF程度が、「音質的」にみた最適値です。実際LPFとして見た場合のCRは、-3dBカットオフ周波数が$f_{cut} = 1/(2 \pi C R) = 13.3\mathrm{kHz}$となり、周波数特性も十分です。
一方、CはRF信号の受信周波数に対して十分に低い必要があります。並列に入る負荷抵抗Rに比べて十分低い値が欲しいところ。AMバンド端の535kHzにおいて、120pFは2.7kΩのインピーダンス。抵抗R=100kΩと比較して、まぁまぁ納得できる低さです。
\begin{eqnarray} C&=&120 \ \mathrm{[pF]} \\ R&=&100 \ \mathrm{[k\Omega]} \\ \end{eqnarray} の条件にて、 \[ CR=12\mathrm{[\mu s]} \] このとき、 \begin{eqnarray} \omega_c CR & = & 40.3 \ (f_c = 535 \mathrm{kHz}) \\ \omega_a CR & = & 0.75 \ (f_a = 10 \mathrm{kHz}) \end{eqnarray} \[ AF\mathrm{(-3dB \ Bw)} = 13.26 \ \mathrm{kHz} \]と、いったところで、大体はいい線を行っているような気がします。何にせよ、このあたりをいかに両立させるかが、ゲルマ/鉱石ラジオの腕の見せ所だと痛感させられます。
4.ネガティブピーククリッピング歪み
別名、尻切れ歪み。
イヤホンの選択やつなぎ方によって発生する歪みです。負荷が抵抗Rだけなら発生はしません。それに加えて音声信号帯域(AF帯)だけに影響する負荷…すなわち、検波回路に増幅回路やイヤホン/ヘッドホンを接続することで、この歪みが発生します。
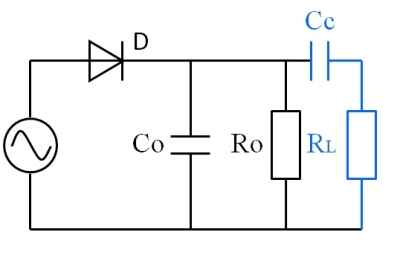
図14.外部の負荷RLを接続した回路
このとき、新たな負荷は直流をカットして音声周波(AF)だけを取り出す場合がほとんどです。図14だと、カップリングキャパシタCcを通じてRLを接続している状態ですし、トランスを利用する場合も、同条件です。
問題はダイオードから見た負荷の状況。DCだとRoのみが負荷となりますし、AFだと、RoとRLが並列になったように見えます、
つまり、AF帯はDCよりも負荷が重くなります。この結果、RF振幅の変動分に応じて、大目の電流がDCよりも流れ、負の電圧まで出力が振れようとします。ですが、ダイオードがあるため、負の出力はカットされてしまい、信号が尻切れとなります。
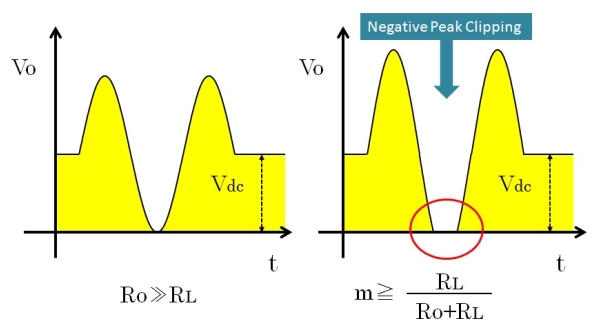
図15.ネガティブピーククリッピングの波形(右)
電子回路的な考えだと、直流負荷線と交流負荷線が異なるというトランジスタ回路によくあるパターンです。実際に、増幅器の最大出力振幅はこれらによって制限されますね。
おお、何と恐ろしい!でも実際にはあまり発生しないので、さほど心配する必要はありません。理由は、同調回路という高いインピーダンスの信号源を使うからです。
発生しやすいのは、変調度が100%に近く、50Ωのような低インピーダンス信号源で、さらに、その信号が十分に大きく、それでいて、AF負荷が大変小さい場合という極端な場合でしょう。
ダイオードの向きを逆にすると、反対に正のピークが切り取られます。なので、この場合はポジティブピーククリッピングと言うべきでしょうが、このあたりをツッこむ人はおりません。あしからず。