3.分布定数回路の基礎方程式を導く
3.1 はじめに
ここでは電気回路モデルから、分布定数回路の基礎方程式を導くまでの計算を行います。このあたりは電気回路というよりも、数学の計算がメインになってしまうかもしれません。
数式は極力、省略しないで、計算過程が分かりやすいよう努めましたが、お気づきの点や、分かりにくい個所がございましたら、メールにてご連絡いただけると幸いです。
3.2 分布定数回路の基本モデル
分布定数回路の電気回路モデルは図3のように、回路全体に分布している電気回路要素を表すため、微小距離で切り取った伝送線路は集中定数回路で近似できるように見えるという前提で成り立っています。
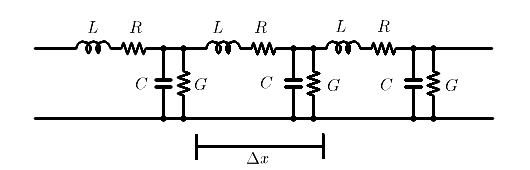
図3 分布定数回路の一般的表現
図3は分布定数回路を近似的に表したものであって、実際にこうなっている訳ではありません。図3と同じものを集中定数回路で組もうとしても、出来上がるのは低域フィルタ(LPF)です。そうなっては、高周波伝送は不可能になりますね。あくまで一様に分布していることが重要で、集中定数のような不連続があってはならないのです。
しかしながら、微分の考え方を使うことで解析が可能となります。無限小の距離ではさしもの分布定数も集中定数的に扱えるようになってきます。次節以降は、そのモデル解析をひたすら続けていくことになります。
3.3 微小区間における等価電気回路モデル
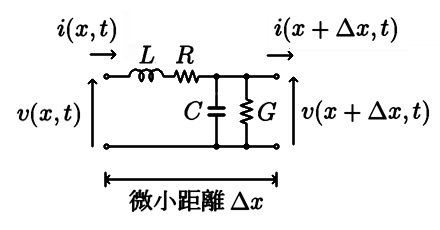
図6 分布定数回路における微小部分の等価電気回路
図3から一部分を抜き出したのが図6の回路です。きわめて微小な距離 \(\Delta x\) の間にLRCGが分布していると考えたものです。この回路モデルに限らずいくつかの等価回路はありますが、結局はこの回路に帰着することになります。
図6における注意点ですが、LRCGはいわゆる普通の電気単位ではなく、単位長あたりの電気単位となります。また、電圧vと電流iはどちらも距離xと時間tの2変数関数 \( v(x,t) \) と \(i(x,t) \) です。
通常の電気回路では時間tのみの関数を考えるので、連立の常微分方程式になり、比較的容易に解くことができます。一方、分布定数回路では距離xの変数も導入されるため、2変数関数となり、その結果、連立の偏微分方程式になってしまいます。
まずは、記号的な定義を先にしておきましょう。
\begin{eqnarray}
v & = & v(x,t) \tag{3.1a} \\
i & = & i(x,t) \tag{3.1b}
\end{eqnarray}
の2つの式が、入力側の電圧および電流の変数とします。そして、出力側の電圧と電流はそれぞれ
\begin{eqnarray}
v_o &=& v(x+\Delta x,t) \tag{3.1c} \\
i_o &=& i(x+\Delta x,t) \tag{3.1d}
\end{eqnarray}
と表記することにします。
3.4 電圧に関する回路方程式
最初は図6を元に、入出力の電位差について方程式を立てることにします。
入出力の電位差を \(\Delta v \) とおけば、
\[
\Delta v = v(x,t)-v(x + \Delta x,t) \tag{3.2}
\]
それから、その電位差が生じる要因である分布抵抗Rの電圧降下は
\[
R \ \Delta x \ i \tag{3.3}
\]
であり、分布インダクタンスLによる電圧降下は
\[
L \ \Delta x \ \pdiffA{i}{t} \tag{3.4}
\]
になります。なお、\(R\) と \(L\) は [Ω]や[H]の単位ではなく、単位長さ当たりの分布量を示しているため、電位差を求めるためには必ず距離を掛ける必要が出てきます。ここでは、微小距離 \( \Delta x \) を掛けています。
式(3.2),(3.3),(3.4)をまとめて、回路方程式を組み立てると
\[
\Delta v = R \ i \ \Delta x + L \ \Delta x \pdiffA{i}{t} \tag{3.5}
\]
という式になります。
ここで、式(3.5)の両辺を\( \Delta x \) で割ります。
\[
\frac{\Delta v}{\Delta x} = R i + L \pdiffA{i}{t} \tag{3.6}
\]
次に、\( \Delta x \to 0\) の極限をとれば、式(3.6)左辺は
\begin{eqnarray}
\lim_{\Delta x \to 0} \frac{\Delta v}{\Delta x}
&=& \lim_{\Delta x \to 0} \frac{v(x,t)-v(x + \Delta x,t)}{\Delta x}\\
&=& -\pdiffA{}{x} v(x,t) \\
&=& -\pdiffA{v}{x} \tag{3.7}
\end{eqnarray}
となって、距離 \( x \) についての偏微分になります。
最終的に式(3.6),(3.7)から、
\[
-\pdiffA{v}{x}= R \ i+ L \pdiffA{i}{t} \tag{3.8}
\]
という、
電圧の距離分布に関する最も基礎的な偏微分方程式が求められます。
距離に応じた電圧降下の傾きは、抵抗による電圧降下に加え、電流の変化に応じたインダクタンスの効果によるという意味です。
一見複雑な表記に見えるかもしれませんが、式(3.8)を電気回路でよく使われる表現(フェーザ表記又はフーリエ変換解)に直すならば、 \(\omega\) を角周波数 \( 2 \pi f\) として
\[
-\frac{dV}{dx}= (R + j\omega L) \ I
\]
という形式であり、より簡便に扱えるものです。(周波数領域表現)
3.5 電流の回路方程式
前節と同様の手順で進めます。まず入出力の電流差分を \(\Delta i\) とおいて、
\[
\Delta i = i(x,t)-i(x+\Delta x,t) \tag{3.9}
\]
としておきます。
そして、分布漏洩コンダクタンス\( G \) による電流の減少量は、
\[
G \ \Delta x \ v_o \tag{3.10}
\]
であり、分布キャパシンタンスCによる電流減少分は
\[
C \ \Delta x \ \pdiffA{v_o}{t} \tag{3.11}
\]
になります。先ほどと違うのは \( C \) と \( G \) にかかる電圧が入力電圧 \( v \) ではなく出力電圧 \( v_o = v(x+\Delta x ,i) \) になっていることです。
結果として、式(3.9),(3.10),(3.11)をまとめた回路方程式は
\[
\Delta i = G \ \Delta x \ v_o + C \ \Delta x \ \pdiffA{v_o}{t} \tag{3.12}
\]
となります。
この式(3.12)を先ほどと同様、両辺を\( \Delta x \) で割り、
\[
\frac{\Delta i}{\Delta x} = G \ v_o + C \ \pdiffA{v_o}{t} \tag{3.13}
\]
とした上で、 \( \Delta x \to 0 \) の極限をとれば、その左辺は
\begin{eqnarray}
\lim_{\Delta x \to 0} \frac{\Delta i}{\Delta x}
&=& \lim_{\Delta x \to 0} \frac{i(x,t)-i(x + \Delta x,t)}{\Delta x}\\
&=& -\pdiffA{}{x} i(x,t) \\
&=& -\pdiffA{i}{x} \tag{3.14}
\end{eqnarray}
と、やはり電流の距離に関する偏微分になります。
次に右辺ですが、先ほどとは異なり極限をとるべき \( \Delta x \)の項があるので、それぞれ、
\begin{eqnarray}
\lim_{\Delta x \to 0} G \ v(x + \Delta x)
&=& G \ v(x,t)\\
&=& G v\tag{3.15}
\end{eqnarray}
\begin{eqnarray}
\lim_{\Delta x \to 0} C \ \pdiffA{}{t} v(x+\Delta x)
&=& C \ \pdiffA{}{t} v(x,t) \\
&=& C \ \pdiffA{v}{t} \tag{3.16}
\end{eqnarray}
と極限値を求めれば、出力電圧 \(v_o\) であった部分が入力電圧 \( v \) に置き換わってくれることになり、とても単純化できます。
結果として求められた電流の距離分布に関する偏微分方程式は
\begin{eqnarray}
-\pdiffA{i}{x} = G v + C \pdiffA{v}{t} \tag {3.16}
\end{eqnarray}
この式(3.16)も分布定数回路における最も基本的な方程式です。
また、フェーザ/フーリエ変換の表現形式に直せば、
\[
-\frac{dI}{dx}= (G + j\omega C) \ V
\]
といったシンプルな形になります。
3.6 回路方程式のまとめ
図6の回路モデルから導出された方程式は、以下の二つの式(2.13)に集約されることがわかりました。二つの式は、それぞれ電圧と電流の距離と時間に関する式です。
\begin{eqnarray}
-\pdiffA{v}{x} &=& R \ i + L \pdiffA{i}{t} \tag{3.8} \\
-\pdiffA{i}{x} &=& G \ v + C \pdiffA{v}{t} \tag{3.16}
\end{eqnarray}
この後は、この二つの式をもとに解析を進めていくことになります。二つだけ…とはいえど、距離xに時間t、加えてLRCGの4定数と変数の種類は多彩そのものですから心配はありません。
次ページへ続く

