1 分布定数回路とは何か
1.1 はじめに
浅瀬野です。このページは分布定数回路についてかつて勉強したことをまとめたものです。学生時代、無線工学や伝送理論を学ぶにあたって、相当苦労したのが分布定数回路でした。問題は何とか解けるけど、どうしてこうなんだろうといった疑問が多かったのもこの理論です。
私自身、頻繁に仕事で使うことは無いのですが、その理論的な考え方は工学の王道ともいえるもので、電磁気学の近似から工学的応用に至るまでの道筋には、かなり学ぶべきところが多いと感じました。
素人が書いた文書ですので、誤っている個所もあるかもしれませんが、お気づきの点がありましたら、ご指摘をいただければ幸いです。
1.2 いったいどんな回路なのか?
分布定数回路というのは、一言でいって距離の概念を導入した電気回路のことです。これと対比をなすのが集中定数回路という用語です。分布したり集中したりする回路とは一体何のことなのでしょうか。(補足:「定数」は『ていすう』が正しい読み方ですが、『じょうすう』と呼ばれることが多いです。その昔「常數」と呼ぶ場合もあった頃の名残でしょう。)
実は集中定数回路というのは、L、C、Rで構成されるごくありふれた電気回路のことを指す用語で、集中というのは、回路素子が空間のある一点に集中している状況を示しています。
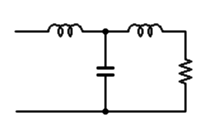
図1.1 集中定数回路の一例
例えば1つの抵抗器を考えると、それは空間的に1箇所へ集中している回路素子です。回路を見て、どこが抵抗でどこがコンデンサなのかボンヤリして区別が付かないなんてことは稀でしょう。ですがLANケーブルなどの伝送路を電気回路で表現しようとしたときはどうでしょうか。電線には抵抗RやインダクタンスL、静電容量Cが確かに存在するのですが、どこにRがあり、どこがCなのかは区別して考えることはできません。
そこで、二つの線(平行2線)からなる伝送ケーブルを考えたとき、ある微小距離ΔxにLCRが詰め込まれている回路を考え、それが無数に縦続接続されていると考えたのが図1.2です。
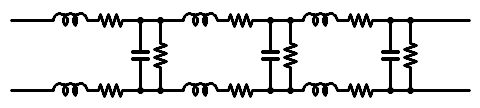
図1.2 分布定数回路の一般的な表現
図2の回路はそのままだと使いにくいので、電気回路の法則を使い、図1.3のようにまとめることもできます。こちらのほうがよく使われる表現です。
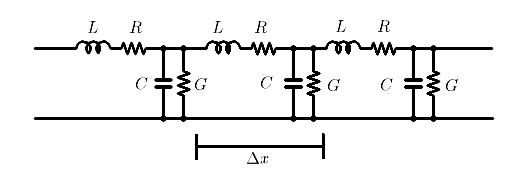
図1.3 分布定数回路を表すのによく使われる表現
このように、回路素子が空間的に分離ができず、全体的に回路定数が分布していると考えられる回路のことを分布定数回路といいます。
1.2 伝送線の電気定数(1次定数)
分布定数回路では、「ここに何[Ω]の素子がある」とはいえないので、1メートルあたりの抵抗、1メートルあたりのインダクタンスといった「単位長さ」あたりの電気定数表現になります。図1.3ではL,R,C,Gの4定数が存在していますが、その理由を平行2線(レッヘル線)伝送路で考えれば以下のように考えてよいでしょう。
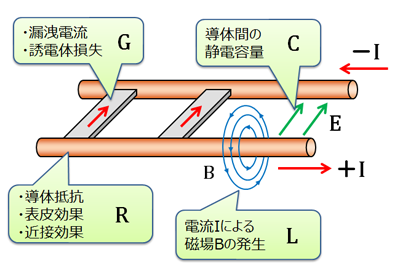
図1.4 平行2線伝送路の図解
単位長は1メートルが標準的ですが、1キロメートルが使われる場合もあります。
L:インダクタンス
電線の自己インダクタンスLは、低周波だとあまり意識する事はありません。しかしながら分布定数回路で欠かせない定数の一つです。
電流が流れている導線には必ず磁束が発生しますが、これは多かれ少なかれ自己インダクタンスを持つということを意味します。通常は、1メートルあたり数μH/m以下の小さい値ですが、線が長くなったり、高周波になると無視できなくなってきます。
なお、この自己インダクタンスは往復分の合計値です。
- インダクタンスの単位
- [H/m] (ヘンリー/メートル)
R:抵抗
抵抗Rは普通の導線が持ってるオーム抵抗のことなので、特に説明は要りませんよね。高周波領域になると表皮効果 (skin effect) や近接効果 (proximity effect) の影響もあり、導体の表面に集中して電流が流れるため、直流よりも大きい抵抗値になります。
なお、この導体抵抗Rは往復分の合計値です。
- 抵抗の単位
- [Ω/m] (オーム/メートル)
C:キャパシタンス
キャパシタンスCは導線が二つあるわけですから、導体が二つ向き合って電位差がある…すなわち一種のコンデンサと見ることができるからです。
- キャパシタンスの単位
- [F/m] (ファラッド/メートル)
G:コンダクタンス
並列コンダクタンスGは導線間の漏洩抵抗に相当するものです。2本の線の間には何らかの絶縁体が置かれるわけですが、それは空気だったり、発泡ポリエチレンだったりと様々な誘電体が考えられます。
実際のケーブルを直流で測定すると、浸水で劣化しているとか、過酷な環境下でない限りは漏洩抵抗はほとんど無く、極めて高い値(数MΩ以上)となることが多いはずです。しかしながら、周波数が上がると絶縁体の誘電損失 ($\tan \delta$) が効いてくることもあってエネルギ損失が大きくなり、この損失を表すためにGが必要になってくるのです。
一般的な絶縁のよい通信線では、角周波数 $\omega = 2 \pi f $を用いて、 \[ G = \omega C \tan \delta \] と表すことができます。
- コンダクタンスの単位
- [S/m] (ジーメンス/メートル)
補足
単位長にはメートルのほか、電話線ではキロメートルも用いられることがあります。
1.3 なぜ分布定数回路を使うのか
1.3.1 電気回路理論の欠点
電気回路の基本的な部品、コイル(インダクタンス)、コンデンサ(キャパシタンス)、抵抗(レジスタンス)は線形素子と呼ばれ、入力と出力が比例する性質があります。(これに対しダイオード、トランジスタは非線形素子です)
これらを組み合わせることで複雑な電気回路を構成していくわけですが、使用する周波数が上がってくると想定外の動作をし始めます。低い周波数では全く問題なかった回路も、挙動が変わってくるのです。
問題の原因は、電気回路理論に「距離」と「波の速度」という概念が無いためです。
1.3.2 思考実験その1
まず、家庭用100[V]コンセントの交流電圧を考えてみましょう。その電圧をスローモーションで見ると、よく知られているような正弦波振動を見ることができます。(もし50[Hz]の電源周波数とすれば、一往復するのに0.02秒かかる計算になります。)
動画1 コンセントの電圧振動
コンセントの電圧は実効値表記のため、瞬時値(最大振幅)は表示電圧の \( \sqrt{2} \) 倍になりますから、+141V~-141Vの間で振動していることになります。
次に、このコンセント用に、数万キロメートルもあるような超長い電線を用意します。普通の電線だと電気抵抗があり、距離が伸びるほど電圧が低下してしまいますが、説明を簡単にするために抵抗がほとんど無い理想的な電線だと仮定してしまいましょう。
そして、100[V] 50[Hz]のコンセントへ差し込んでスイッチをオンしてみます。すると、スイッチオンの瞬間から電圧は電線内を伝わっていきます。
電圧の伝達速度はだいたい光速に近いので、およそ秒速30万キロメートル( $ 3 \times 10^{8} \mathrm{[m/s]} $ )とします。
波の速度v、周波数f、波長λの間には \begin{align} v=f \lambda \end{align} という関係式がありますので、交流50ヘルツの波長λを計算すると、 \begin{align} \lambda = \frac{v}{f} = \frac{3 \times 10^{8}}{50} =6 \times 10^{6} \ \mathrm{[m]} \end{align} つまり、波長が6千キロメートル[注2]にもなる計算です。
その電圧が伝わる様子を示したのが、下の動画2です。
動画2 超長い電線をコンセントに接続
この動画では、0.06秒だけスイッチを入れたときの波が伝わる様子を表しています。そして、この電圧が伝わっていく様子の「ある瞬間」を切り取ったのが図1.5です。
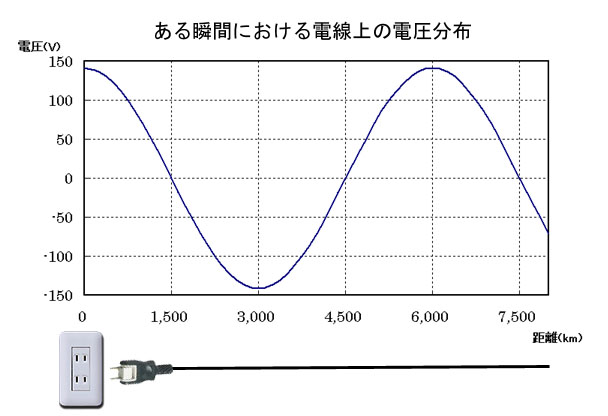
図1.5 ある瞬間の電線上の交流電圧分布
このとき、コンセントでは141Vの電圧ですが、1,500km離れた場所では0V、3,000kmでは-141Vと全く異なる電圧になっていることが分かると思います。
「同時刻」にコンセントの差込み口で計った電圧と、何千km離れた場所で計った電圧は異なってくるのです。このことを位相が異なるとも表現します。
基本的な電気回路理論に従えば、位相を変えるためにコンデンサやコイルが無くてはいけません。しかし、そんな部品を取り付けてもいないのに、距離に応じてドンドン位相が狂っていく恐ろしい状況なのです。
が、普段はこんなことは考えなくてもOKです。当然なことに、日常で扱う電気の範囲は、家庭内や工場内など「たかだか数十メートル」の距離です。個人で何千キロメートルも扱うことはあり得ませんので、普段は上記のことを気にせず使うことができるわけですね。
超厳密に考えれば、10mの電線コードでも位相の遅れがあるんですが、計算してみると100[V]が99.999999994517[V]、位相が0.006[度]遅れになる程度なので、無視した方が幸せに暮せるってもんです。
ここで注意しなければならないことは、場所によって電圧の瞬時値は違ってくるものの、電圧の実効値は変わらないことです。実効値は、いつ、どこの場所でも100[V]になります。これは、実効値というものが瞬間の値ではなく、交流1周期の平均量だからです。
1.3.3 思考実験その2
では、周波数が300[MHz]ならどうでしょうか?
1波長は1メートルです。そうなるとコンセントの電圧とほんの数十センチ離れたところの瞬時電圧は大きく食い違ってきます。 コンセントである瞬間に100Vの電圧なのに、50cm離れた場所の電圧は10V、80cmの場所は-50V、20cmの場所は40V…といった感じです。
これでは、回路の動作が全然把握できません!
例えば、ちょっと離れた場所にコンデンサなんかを置いたときの挙動は一体全体どうなるのか? 少なくとも普通の電気回路理論では歯が立たない問題になってきます。
携帯電話の周波数、2GHz(波長=15cm)ぐらいになると、もうミリ単位でこの手の問題が発生してしまうことは明らかです。
1.3.4 分布定数回路の意義
このように、高周波における問題点を克服するために出来上がったのが分布定数回路理論です。分布定数回路では、距離の概念を導入して、高周波の伝送問題を電気回路の一種として扱うことができます。
本来は電磁気学のマクスウェル方程式を解いていくのが厳密な解答ですが、より簡単に、電気回路の延長線上で扱えるのがこの理論の魅力です。
分布定数回路はマクスウェル方程式を簡単化したものであると同時に、一般的な電気回路理論を拡張したものと考えられます。
| - | 集中定数回路 (電気回路) |
分布定数回路 | マクスウェル方程式 |
|---|---|---|---|
| 難易度 | やさしい | やや難しい | かなり難しい |
| 適用範囲 | 小さな低周波回路 | 単純な伝送線路(TEM波) 高周波の電子回路 長大な線路をもつ低周波回路 |
何でもOK |
1.3.5 分布定数回路の適用範囲
分布定数回路理論が威力を発揮するのは、波長を無視できない大きさを有する電気回路です。扱う波長が回路や線路内で無視できない場合というのどの程度か?とよく議論になるところですが、ここは設計思想によって大きく変わる部分です。
一般的には配線長が波長の数%~数十%程度になるような条件が多いようです。周波数が高ければもちろん、周波数が低くても長距離送電線のような場合にも分布定数回路が適用されます。
つまるところ、波長と配線長との比が重要な判断指標となります。
また、細かい話になりますが電磁波の伝送モードに影響を受けます。電磁波の基本的な伝搬形態であるTEM波[3]においては、適用が容易です。これは、元々TEMを仮定した式になっているからです。
付け加えると、回路を構成する要素(線の太さや間隔)が波長を無視できない場合は、適用できません。この場合は、マクスウェル方程式から解かなければなりません。
1.4 歴史的な背景
こういった電気回路の発展形としての伝送線路理論は、19世紀後半になって研究されたようです。もともと、電信(モールス通信)用の線路は、適当に張られているだけで、分布定数回路の考え方など微塵もなかったのですが、距離が短い通信や、低速度の伝送に関しては、何ら問題は起きませんでした。
しかし、問題の端緒となったのは海底ケーブルの敷設です(1860年前後)。様々な困難を克服してドーバー海峡や大西洋などに海底電信線が敷設されるようになると、波形が歪み、高速度の通信ができなくなりました。様々に無駄な工夫を凝らすことになったようです
例えば、電圧を上げればいいんじゃないか・・・と、2000Vぐらいの高電圧をかけて馬鹿高い海底線路を絶縁破壊でお釈迦にしてしまうような有様。
で、イギリス政府と電信会社によるプロジェクトが発足し、解析が行われた結果、分布定数回路理論の原形が出来上がりました。特にケルビン卿(Sir W.Thomson)の解析がとても素晴らしいものだったとか。彼の解析したケーブルはトムソン線路(CR線路)と呼ばれるもので、LとGを無いものとして解析したものでした。
この場合、電圧の伝達速度が無限大となってしまう欠点はあるのですが、静電容量の大きなケーブルを使って、低速度のモールス通信をする際には、かなりの成功をおさめることになったわけです。
その後、独学の天才物理学者、オリバー・ヘビサイド(O.Heaviside)が理論的な発展を進め、LRCGの4定数を使った電信方程式と呼ばれる連立偏微分方程式が発表されたのは1881年頃のようです。
1.5 補足事項
(注釈1) 削除
(注釈2) 電線の電気が流れる速さ
波の伝搬速度が30万km毎秒(=真空中の光速と同じ)という条件で算出していますが、実は何割か遅くなります。その結果、波長も短くなります。
実際のところ、電線やケーブルに電気が流れるというのは不正確で、電波(電磁波)が、電線やケーブルをたどって(閉じ込められて)伝搬していくというのが正しい表現です。
電磁波が導線をガイドとして伝わっているとも言えますし、電波が電線にまとわり付くとも言えると思います。
通常のコンセントの電源も、100Vの実効値をもった、50Hz~60Hzの電波が、配電線を通じて送られていると言うこともできます。ですから、コンセントにアンテナをつなぐと簡単な送信機になってしまいます。(もっとも、マトモに動かすにはかなりの大きさですが)あんまり想像できませんけどね・・・。実際潜水艦との水中通信に使われる超長波では45Hz,76Hz(米海軍),82Hz(露海軍)などのコンセント並みの周波数で、20km以上の特殊アンテナを張って実験していました。
義務教育までは、電子が光速で移動するみたいに教わっていましたが、ほんとの速度は秒速数センチ。電線の電気というものが、電界と磁界の波動で、導体をガイドにして伝わっていくもの・・・と理解したのは電磁気学を学んでからです。
それで、電気が光速で伝わるという話をしましたが。現実的にはもっと遅い速さになります。どれぐらい遅くなるのかは、伝送路の電気的特性(形状・材質)で決定され、普通の同軸ケーブルだと、光速の60%から90%ぐらいです。
波動の性質から、通常、周波数は変化しないので、波長=速度÷周波数により、当然波長も短くなってしまいます。そこで、同軸ケーブルの場合、光速で伝送されると考えると不都合なので電気長とか波長短縮率という考え方が使われてます。だいたい元の波長に60~90%をかけた値で、同軸ケーブル内の波長と一致します。
(注釈3) TEM波
TEM波 (Transverse Electro Magnetic Wave) とは、いわゆる平面波のことです。電磁波の進行方向に電磁界ベクトル成分の無い状態のことを指します。分布定数回路はTEM波が伝送される線路を電気回路で近似した理論とも。
x-y-zの3次元直角座標系で、z方向に進む電磁波を考えた場合、z軸方向の電場Ez=0、磁界Hz=0の場合をTEM、Ez=0,Hz≠0の場合はTE(Transverse Electric Wave)波、Ez≠0,Hz=0の場合はTM(Transverse Magnetic Wave) 波 、Ez≠0、Hz≠0で混成波(Hybrid Wave) と分類されます。
Transverseというのは、進行方向の横断面を指す用語ですから、頭にTが付いたときは、ケーブルや導波管などをぶった切ったときの断面に対して、ちょうど並行となる電磁界ベクトル成分に注目していることになります。
逆に、進行方向(z軸方向)にどんな成分があるかをもって呼び名としたものにE波、H波、EH波という呼び方もあるんです。
- H波----(TE波)
- E波----(TM波)
- EH波---(混成波)
これらの名前の違いは、どこを基準にして特徴を捉えているかの違いなんですね。
ちょっと旧い教科書になると、いろいろ呼び名がでてくるので、覚えていて損はないような気がします。
で、解析的には、TEM波はEx,Ey,Hx,Hyの四成分しか求めなくていいので、結構楽チンであったりします。よくマクスウェル方程式から電磁波の存在を導くのに、平面波を仮定してTEM波を求めさせるのは、この楽チンさのせいであると思われます。
平行2線伝送回路、同軸形伝送線路、平行板伝送線路、ストリップライン・・などはTEM波が主であり、また、高圧送電線もTEM波が主のため、比較的解析がしやすい。
導波管の場合は、TEM波が存在できないことが、数式で証明されてたりするので要注意(かも)。