ここでは、ダランベールの解を求めるのに使った「求積法」以外の方法で、電信方程式を解いていくことにします。多くの教科書では複素数を使ったフェーザ法(ベクトル記号法)での説明に入ることが多いのですが、ちょっと遠回りして様子を見ることにします。
ただ、この辺あまり深入りすると数学基礎論(群とか、超関数とか、コンパクトな台とか、なんとかシュワルツ空間とか...etc.)、の襲撃が予想されるので、ほどほどにしておくつもりです。
フーリエ変換って何?と言われても、それを説明するのは、私にとって大変難しい・・・というよりは不可能に近いことなので、ここは単なる道具として使っていくことにします。
まぁ、電気屋さんとしてなら、時間tで表した信号を、周波数成分ωで表す信号に変換するっていう程度でもよいかもしれません。
※なお、下記の計算手順は形式的なもので、数学的には厳密なものではありません。
下記の無損失電信方程式(4.1)をフーリエ変換を使って、解いていきます。とりあえず電圧だけでやっていきましょう。
・・・(4.1)
ここで、電圧関数v(x,t)がフーリエ変換できて、その変換対を V(x,ω) とします。
時間tを角周波数ωの表現へ変換してあげるわけです。
これを式で表すと
・・・(7.1)
になります。
式(4.1)の両辺をフーリエ変換すると、
・・・(7.2)
となり(補足1)、時間変数tの偏微分が消え、左辺が常微分にできるので、まとめると
・・・(7.3)
(7.3)は一般的な同次の2階の常微分方程式(調和振動)なので、ωを定数として扱えて、
Vの解は公式(補足2)から
・・・(7.4)
と導かれます。A(ω),B(ω)は積分定数です。
次に、下のフーリエ変換公式(7.5)・・・時間推移則(補足1)を利用して、式(7.4)を書き直してみます。
・・・(7.5)
式(7.4)の(√LC) x は、式(7.5)のtoに置き換えられるので、A(ω)の部分をf1、B(ω)の部分をf2とすることで、式(7.5)は結局、
・・・(7.6)
の形になります。どことなく見た覚えのあるカタチです。さらに、式(7.6)をLCが定数であることに注意して変形していくと、
・・・(7.7)
何とか式(4.15)ダランベール解と同じ結果になりました。
![]() ・・・(4.15)
・・・(4.15)
つまるところ、フーリエ変換すると、小難しい微積分抜きのお手軽さで自然に解が導かれるということなんです。
フーリエ変換する最大の利点は、ややこしくなる原因の微分・積分がただの掛け算・割り算に置き換えられことです。ラプラス変換でも同じ利点が生まれますが、こちらはt=0で始まる現象にしか適用できない縛りがあります(その代わりに、扱える関数の範囲が広くなる)
これが記号的計算法と呼ばれるフェーザ法(Phasor)の土台的な部分になります。
注意点は、上記の計算方法がかなり大雑把で厳密なものではないことです。かなり形式的な計算方法になります。(計算の詳細と問題点は補足3にあります。)
時間関数 f(t)のフーリエ積分をF(ω)とします。ただし、-∞<t<+∞です。
![]()
このとき、f(t)の1階の微分係数 f'(t) = df(t)/dt のフーリエ変換と
2階の微分係数 f''(t) = d2f(t)/dt2 のフーリエ変換はそれぞれ
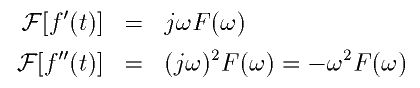
となり、時間領域での微分は、フーリエ変換にjωを単純にかけるだけとなります。
また、フーリエ変換には線形性があるため、f(t)にかけれらた定数はそのままになります。
2階の線形非同次の微分方程式
の解は、A、Bを定数として
となります。当然jは虚数単位です。導出方法など詳しくは微分方程式の教科書を参照してください。
実際、下記のようにf(x)を2回微分すると、解になっていることが簡単に確かめられます。
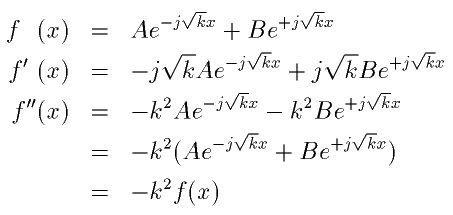
時間領域の関数f(t)を周波数表現F(ω)へ変換する、フーリエ積分の定義は
電圧関数v(x,t)はフーリエ積分ができるとして、その値を大文字でV(x,ω)とします。
無損失のの電信方程式
・・・(式4.1)
の左辺側をフーリエ変換すると、
ここでは、積分と微分の順序交換の定理を使用し、偏微分演算子∂2/∂x2を積分の外に出してしまう操作によって、ωは定数とみなせて、偏微分が通常の微分とみなせます。
(式4.1)の右辺側はexp(-jωt)とx(x,t)の二つのtを含む変数があるので、部分積分を繰り返すのが一般的な解法です。
この方法(逐次部分積分)では、積分の外に出した部分が0になるという仮定をしています。
そのためには、電圧関数v(x,t)が[t→∞,-∞]で十分に小さくならなくてはいけないのですが、必ずしもそれが保証されているわけではなく、また、v(x,t)の時間極限で値が0になるというのが、物理的に今ひとつ想像できない部分でもあります。(無損失線路ではそもそも達成できない?)
そのため、普通は距離xに対するフーリエ変換をし、電圧vが十分遠方で0となる条件を仮定することで、絶対積分条件∫[∞,-∞]|f(t)| dt
<∞ をなるべく自然に回避しています。
| 技術の渚>分布定数回路7 | ←前へ|次へ→ |
作成:浅瀬野,初出:2008/Nov/30,最終更新:2008/Nov/30