AM放送波(中波)の電波伝搬について
1 はじめに
AM放送で使用されている電波帯域は、526.5kHz から 1606.5kHz[1]です。
この帯域は中波(MF: Middle Frequency , 300kHz-3000kHz)と呼ばれる周波数で、FM放送やTV放送などで用いるVHF帯またはUHF帯とは全く異なる伝わり方をします。
このページではゲルマラジオ/鉱石ラジオの受信を目的とし、放送局からの距離・出力などから受信地点の電界強度を推測する方法について、最近調べたことを説明していきたいと思います。
2 電波の伝わり方
電波の伝わり方は伝搬モードと呼ばれ、使用する電波の周波数や距離などによって様々に変化します。また呼称も同じようなものがいくつもあり、どこに着目するかで変わってきますが、おおきく分けると以下の二つに分けることができます。
- (1) 地上波(Ground Wave)
- (2) 上空波(Sky Wave)
上空波は電離層波(Ionospheric Wave)とも呼ばれ、地上100km以上にあるイオン層による反射波、散乱波を指します。
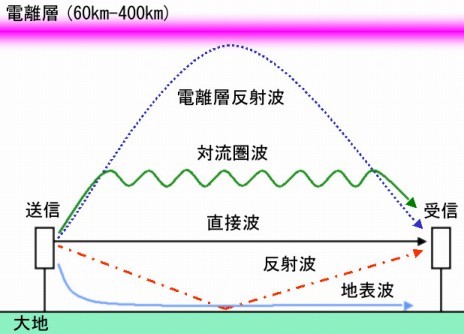
図1 電波の伝わり方
2.1 地上波
地上波とは、地上から上空12kmぐらいまでの空間を伝搬する電波のことを言い、主な分類は以下の4種類です。
- 直接波(Direct Wave)
- 反射波(Ground Reflected Wave)
- 対流圏波(Tropospheric Wave)
- 地表波(Surface Wave)
この他にも、潜水艦通信に利用されるエバネッセント波などもありますが、これは置いときます。
「直接波」は、送信点から、受信点まで直接届く電波です。最もわかりやすい伝搬モードですね。
「反射波」とは、送信アンテナから大地や海面で一度反射されて受信点に届く電波のことを言います。TV電波で使用するVHF・UHF帯では、この二つの成分を合わせたものになります。
「対流圏波」とは、大気の状態や気象状況によって電波が屈折、反射、散乱を受けて受信点に届く電波のことを言います。UHF以上のマイクロ波通信では特に影響を受けることが多く、積極的に使用する場合もあります。なお対流圏というのは聞き慣れない用語ですが、対流圏より上のことを「成層圏」と呼んでいます。こちらはジェット機が飛行する高度なので、聞き馴染みもあると思います。
「地表波」とは、大地表面や海面に沿って伝わる電波のことです。大地上付近のみに存在する成分で、後で詳しく述べますが、AM放送の伝搬はこの地表波が主となります。
地表波を除き、空間波(Space Wave)と呼ばれることもありますが、後述する電離層波の方が空間波と呼ばれることが多く、非常に紛らわしい用語です。上記の他にも、山岳等での回折現象による回折波もあります。こちらはV・UHF以上の周波数での伝搬モードなので説明は割愛します。
2.2上空波(電離層波)
電離層(ionosphere)は、地上約60km付近から500km程度に存在するイオンの層で[2]、電波的な性質からD層、E層、Es層(スポラディクE層)、F層に分類されています。
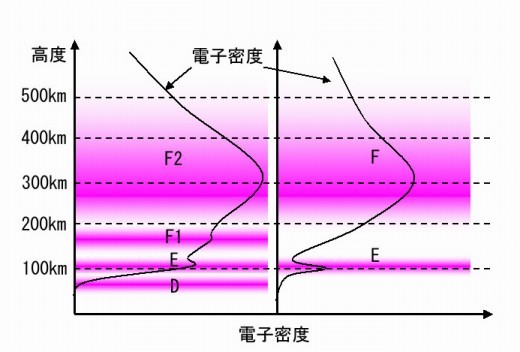
図2 電離層の状態(左が昼間、右が夜間) [2]
「D層」は60km~90kmにある層で、昼間のみ存在します。中波以上の電波に対しては減衰層として働き、周波数が低いほど減衰が激しくなる性質があります。(ただし、長波帯に対しては反射層として働く)。
「E層」は90km~130kmにある層で、昼夜問わず存在します。中波の電波に対しては反射層として働き、AMラジオの遠距離到達をサポートするナイスな存在です。しかしながら、昼間はD層が邪魔をするために、E層に達するまでに大きく電波が減衰し、反射後ももう一度D層を通過するので、事実上、昼間の遠距離伝搬はありません。夜になると遠くのAMラジオ局が聞えるのは、ひとえにE層の存在があることと、そして、夜間だけD層が消滅してくれることが原因です。
「F層」は130km~1,000kmに存在する層で、昼間にはF1層(130~210km)とF2層(210km~1,000km)に分離します。電波的には約500kmぐらいが興味の対象です。短波通信では、主にF2層(電子密度のピークは300km前後)を利用していますが、短波帯の電波がE層を通過する際には、F1層もそのまま通過してしまうため伝搬上は興味の対象外です。
上記の各層の状態は太陽活動、地域、季節、時刻によって大きく変化するため、かなり不安定要素が大きく、現在のように国際的な光ファイバ網、衛星通信網が発達するようになってからは、電離層を利用した通信は傍流となりつつあるのが現状です。
例えば、F1層は冬季になると明瞭に現れません。Es層に至っては常時発生するものではなく、突発的に発生します。Es層が世界で最も発生しやすい期間・地域は夏季の日本付近です。(なお、Es層は夜間の中波伝搬に影響を与えるようです[7])
他にも太陽の活動(フレア現象等)に伴うX線、荷電粒子などの放出が地球電離圏に大きな影響を与え、デリンジャ現象、磁気嵐、オーロラの発生などを引き起こします。いずれの現象も電離層通信に障害を与える要因です。
このように、不安定な要因を抱えつつも、夜間のAM放送に影響を与えるため電離層は無視できない存在です。
2.2.1 補足:電離層でなぜ電波が反射するか
電離層が電波を跳ね返すのは何故か?小学校の頃、電離層の存在を知った時に一番悩んだのがこの問題でした。つまるところ、「自由電子がたくさん詰まっている空間」は電波を跳ね返すというのが答えです。
いちばんわかり易いのは金属でしょうか。金属は電波を効率よく反射し、電気を通しますが、これは自由電子が非常にたくさんあるからです。もっとも、電離層は金属のようにちょいちょいと電流を流すわけにはいきませんが、それなりに導電性があり、マクロに見ると相当量の電流(電離層電流)を流しているそうです。
2.2.2 余談:電離層発見の歴史
電離層の存在が予測されたのは電波の発見よりも前だったようです。地球の磁場(地磁気)は1日の間に規則正しい変化(日周変化)が古くから観測されていたのですが、その原因は大気上層部の導電層にあるとしたスチュワート(B.Stuart)の理論(1878)が最初でした。
次に無線通信が実用の域に達した1902年、ケネリー(A.E.Kennelly)とヘビサイド(O.Heaviside)がそれぞれ独立に電離層の存在を提唱しました。これは、マルコーニ(G.Marconi)による1901年の大西洋横断通信を説明するために導入したものです。電離層には別名でKH層(ケネリー・ヘビサイド層)とも呼ばれます。
ケネリーは電離層の高さを約90kmと計算していますが、これは現在のE層にあたるものです。
1924年になって、アップルトン(Sir E.Appleton)とその助手バーネット(M.A.F.Barnet)によって、その存在が完全に証明されました。その方法は放送局(BBC)の協力のもと、ゆっくりと周波数を変化させた放送波によって生じる、地上波と電離層反射波の位相干渉を利用して、電離層の高さを求めるものでした。(約90km)
ほぼ同時期の1925年~1926年、カーネギー研究所のブライト(G.Breit)とチューブ(M.Tube)らによって現代のパルスレーダと全く同様の手法をもって、その高さが直接計測されるようになります。このときF層の存在も発見されました。彼らはレーダの祖としても知られています。軍事上の応用は電離層計測器に飛行機が探知されることがきっかけだったようです。
なお、電離層にA,B,C層が無い理由は、アップルトンがE層反射波を電界強度(Electric field strenght)の記号にちなんで、Eとメモしたのが原因のようです。E層の反射より高い高度の反射波をFと記号し、E層反射波よりも低い高度での反射波をDとしたのです。
3.AM放送電波(中波)の伝わり方
写真1で紅白に塗られた鉄塔がアンテナ本体で、周囲に張られているのは支線です。
前節では、一般的な電波伝搬の分類をしましたが、AM放送電波は実質的に地表波と電離層波のみとなります。
AMラジオの電波(中波)に限っていえば、送信アンテナと受信アンテナ間では直接電波が通じているわけではありません。もちろん放送局のすぐ近くであればそう考えても良いのですが、数kmを超えたあたりで地表波が支配的になると考えられます。
中波の波長は数百mと大きく、アンテナは地上に直接設置された垂直接地形式のアンテナが利用されています(写真1の例)。
テレビ放送のように水平アンテナが使われていない理由は、水平偏波の性質にあります。水平偏波を地表波伝搬モードで使用すると著しく減衰してしまうのです。大地に対して電界が水平となることで、大地に適度な電流が流れて損失が大きくなりやすいからです。これに対してV/UHF帯では直接波と反射波が主伝搬であり、水平偏波であっても支障はありません。
一方、ラジオ受信機を設置する高さは、常識的に考えて地上数十mが限度でしょう。このように送信側、受信側ともに(波長に対して)低い地上高で使用する条件になると、直接波と反射波が互いに打ち消しあい、結果として地表波成分のみが残るのです[3][4][5]。
地表波は減衰が大きいので、陸上における中波帯では実用上200kmあたりが限界と考えられます。これ以上の距離では夜間の電離層伝搬が主となります。
一例として民放局最大クラスの100kW出力局であるTBSラジオ(埼玉県戸田市氷川町;北緯35度48分、東経139度40分付近)から送出される電波の聴取区域には、福島県郡山市(北緯37度24分、東経140度22分付近)が入っています[6]。距離は約190kmです。
なお、「AM放送の聴取区域」は法律上0.25[mV/m]以上の電界強度がある地域を指していますので[8]、高性能なアンテナと受信機を用いれば、到達距離はもっと伸びるはずです。
ゲルマラジオであれば、なおさら近距離しか(せいぜい40~50km前後か?)聞えないはずです。実際に「昼間」にAMラジオを聞いてみても、その地域近辺の放送局しか聞えません。
一方で、電離層波は夜間しか関係ありませんが、ゲルマラジオで入感することもあるものの、ある程度のアンテナを使用したときに限られると思います。一般的にゲルマラジオで聴取可能な放送局は、近郊の放送局が多いと思いますので、まずは、地表波に絞って議論を進めたいと思います。
4.完全導体の平面大地の電界強度(簡易法)
この節では、地球の大地の曲がりを考慮しない、垂直接地アンテナから放射された電波の強さの計算方法について紹介していきます。
4.1 基本事項
電界強度は、アンテナからの放射電力Pのルートに比例して増加します。これは電界強度が電波のエネルギー(電力)に対して、電圧に相当する量だからです。
そして、距離が離れるほど弱くなりますが、距離dに直接反比例します。
例)P=100[W]の放射電力のアンテナがあり、d=1[km]の距離で電界強度を測定すると、E=1[V/m]であったとする。このとき、
(1)10倍離れた距離(10km地点)での電界強度は、1/10に減衰するので、E=0.1[V/m]
(2)出力を2倍の200Wに増力したときの電界強度は\( \sqrt{2} \)倍となり、\( E=1.41 \mathrm{[V/m]} \)
(3)2kmの距離で、4倍の400Wのとき、\( E = \sqrt{4} \times \frac{1}{2} = \mathrm{1[V/m]} \)
となります。
4.2 完全導体の大地とは?
完全導体の大地とは、大地が非常によく電気を通すような条件です。例えて言うなら、銅板や鉄板を広く敷き詰めることに相当する条件なのですが、現実の大地はそれほど電気を通しやすい物質ではありません。
銅の体積抵抗率は、1.8×10-8[Ω⋅m]程度ですが、実際の大地では10~1000[Ω⋅m]前後であり、相当にかけ離れています。ですので、ここで扱う計算方法は、あくまで目安を得るための簡易的な方法です。
なお、大地抵抗率は地質によって大きく異なります。砂漠地帯、山岳の岩石地帯になると非常に高くなり、湿地帯では小さくなります。関東地域では、100[Ω⋅m]ぐらいで考えておくとちょうど良いでしょう。
(参考になるサイト:(株)サンコーシヤ 日本の大地抵抗率地図)
4.3 前提条件
ここで、計算するアンテナは
- アンテナ本体や接地抵抗による損失は無視する。(効率≒100%)
- 指向性を持たない・・・水平面指向性は無いとする。この仮定は、全ての放送局に当てはまるものではなく、一部の放送局では指向性をもたせている場合があります。
- アンテナは線状で、細い導体であること。一般の太い導体を利用したアンテナとはやや異なります。
という条件で計算します。あまり突き詰めると、かなり難しい領域に入ってしまいそうなのでこのあたりで近似してしまうことにしました。
(備考)一般の中波送信アンテナは、トップローディングアンテナとして頂上に容量環と呼ばれるコンデンサが付いていますが、この容量環によってアンテナ高を小さくすることができます。ただし、放射特性についてはあまり知らないので、容量環を無いものとして計算しました。
4.4 1/4波長 垂直接地アンテナによる電界強度
平面大地上に設置された、0.25波長(λ/4)の垂直接地アンテナの電界強度E [V/m]は \[ E=9.9 \frac{\sqrt{P}}{d} \ \mathrm{[V/m]} \tag{1} \]
ここで、P[W]はアンテナ放射電力、d[m]はアンテナからの距離です。
この電界強度は大地表面上の値で、上空になると指向性があるのでやや異なりますがが、一般的にはこれで十分です。
ここで使いやすいように、電界強度の単位を[mV/m]、距離[km]、電力を[kW]に直すと、 \[ E=313 \frac{\sqrt{P_{(kW)}}}{d_{(km)}} \ \mathrm{[mV/m]} \tag{2} \] と表すこともできます。1[kW]の放送局から、1[km]離れた場所での電界強度は313[mV/m]ということになります。
4.5 0.53波長 垂直接地アンテナによる電界強度
0.53波長(0.53λ)の長さを有する接地アンテナは、中波送信用にもっとも適したアンテナです。ゲインが比較的大きく、地表における電界強度は1/4波長アンテナに比べて約1.2倍(ゲインは1.6)に増加します。
もっと長さを伸ばせば0.64波長(5/8λ)でゲインが最大(G=2)となり、V/UHF帯ではよく利用される長さなのですが、大地方向以外に高角度の不要放射が出てしまうのが欠点です。
この上空高く放射されてしまった電波は、夜間、電離層によって反射され、地上波と相互干渉してしまう原因になります(近距離フェージング)。そのため。0.53波長が最も良いとされています。
その他にも、1/4波長アンテナに比べて給電点インピーダンスが高く、電圧給電するために接地損失が最小になるという利点もあります。
平面大地上に設置された、0.53波長の垂直接地アンテナの電界強度E[mV/m]は \[ E=12.5 \frac{\sqrt{P}}{d} \ \mathrm{[V/m]} \tag{3} \]
先の1/4波長アンテナと同じように、実用単位に変換すれば \[ E=396 \frac{\sqrt{P_{(kW)}}}{d_{(km)}} \ \mathrm{[mV/m]} \tag{4} \]
となります。
4.6 計算例
(Q1)0.53波長のアンテナを使用する放送局は、出力100[kW]である。受信点までの距離が20[km]であるとき、受信点の電界強度(mV/mを求めよ。
(A1) \[ E = 396 \times \frac{\sqrt{100}}{20} = \frac{396 \times 10}{20} = 198 \ \rm{[mV/m]} \]
5.実際の平面大地における電界強度(Sommerfeld~Nortonの方法)
前節までの計算は、大地が完全導体である条件で計算されたものでした。ですが、実際には大地は誘電率と有限の抵抗率(導電率)をもっています。
その抵抗によって、地表波は大地によってエネルギの損失を受け、次第に減衰していってしまうのです。簡単に言えば、抵抗が極めて小さい大地(例えば海水)であると電波は地表に侵入できず、低損失な伝搬路になります。
5.1 何となく歴史
歴史的には、1909年のゾンマーフェルト(A.Sommerfeld)の論文「無線電信における電波伝搬(On the propagation of waves in wireless telegraphy)」から始まるようです。それ以前はツェネック(J.Zenneck)が表面波について初めて論じたようですが、実用的なものではないこともあり、工学的な知見はそれほど多くはなかったようです。(地表波の電界の傾きなどはこれに拠るところがあるみたい。)
以降にこの種の問題を扱う学者さんが、わんさかいらっしゃったようです。ちょっと調べただけで
- ワトソン(G.N.Watson:1918)
- ワイル(Weyl:1919)
- ニーセン(K.F.Niessen:1930)
- ファン・デル・ポール(B.van del Pol)
- ブレマー(H.Bremmer)
- ノートン(K.A.Norton)
- ミリントン(G.Millington)
- 古津 宏一(K.Furutsu)
- キング(J.R.King)
- ウェイト(J.R.Wait)
・・・などなど、お歴々のお名前が挙がってきます。
今使われている「古典理論」は、実用的な論文にまとめたノートン先生の功績のようです。ノートンは、伝搬モードを表面波によるものと、直接波と反射波成分によるものに分けて考えたとともに、計算図表を多く残してくれました。
ここでは、ノートン先生ご紹介の方法[9]による電界強度の計算をしていきます。
5.2 減衰係数関数と数値距離
4節で計算した電界強度は、実現できる最大の電界強度として扱われます。ここで、減衰関数Aは \[ E = E_0 \ |A| \tag{5} \] で定義され、Eoは4節で計算した完全導体大地の電界強度です。
Aは絶対値記号がついていますが、これはAが複素数であるためです。|A|の最大値は1で最小値は0となり、E0よりどれだけ減衰するかを表していることになります。
次に減衰係数Aの値ですが、垂直偏波の場合、 \begin{eqnarray} A = 1 + j \sqrt{\pi p_1} e^{-p_1} \ \mathrm{{erfc}} (-j \sqrt{p_1}) \tag{6} \end{eqnarray} であり、また式(6)の各変数は、 \begin{eqnarray} p_1 & = & p \ e^{jb} \\ p & = & \frac{\pi}{\epsilon_r +1} \frac{r}{\lambda} \sin b = \frac{\pi}{x} \frac{r}{\lambda} \cos b \\ b & = & \tan^{-1} \ \left( \frac{\epsilon_r +1 }{x} \right) \\ x & = & \frac{\sigma}{\omega \epsilon_0} \simeq \frac{1.8 \times 10^4 \sigma}{f_{MHz}} = 60 \sigma \lambda \end{eqnarray} で表される、かなり見た目にも複雑な関数になります。ぎゃひー
ここで、p1は数値距離、rは距離[m]、λは波長[m]、εrは大地の比誘電率、σは大地の導電率[S/m]です。また、jは虚数単位でj2=-1です。
減衰関数Aは数値距離p1(numerical distance)の関数であり、ゾンマーフェルトによって導入された距離に比例した無単位の量に従います。距離に比例するにもかかわらず、無単位なので数値距離と呼ばれています。
なお、erfcは、余誤差関数または補誤差関数と呼ばれる特殊関数[13][14]で、次式で定義されます。 \[ \mathrm{erfc}(z) = \frac{2}{\sqrt{\pi}} \int^{\infty}_{z} e^{-t^{2}} \ dt \tag{7} \]
erfc自体は何とエクセルにも「相補誤差関数」という名前で実装されているのですが、積分路が実数軸上だけではないのでエクセルではさすがにお手上げです。
以上の計算は、平面大地の厳密な減衰関数ですが、解くにはコンピュータでの数値計算に頼ることになります。しかしながら、この論文[9][10]は電子計算機が無い時代のものなので、幾つかの近似式が提示されています。次節では、近似解法とグラフを紹介していきます。
なお、補誤差関数erfc(z)は、かなり計算しにくい関数でした・・・。
5.3 適用限界
式(6)は、平面大地に対しての解です。しかし実際の地球は球面なので、平面として扱える距離には制限があります。文献[5]によると、近似できる距離r(max)は \[ r_{max}= \frac{80_{km}}{\sqrt[3]{f_{MHz}}} \tag{8} \] です。また、文献[12]では(8)式の定数を66.94kmとしています。(根拠ワカランですが)
AM放送帯域で考えれば、おおむね、70km前後まではこの式が適用できることになります。(参考:500kHz:100km、1000kHz:80km、1600kHz:68km)
5.4 数値距離の近似式
日本における中波での数値距離はおおむね実数値をとります(つまりb=0°に近くなる)これは、日本の大地が比較的水分量の多い土壌であるためです。
数値距離の偏角bは \[ b = \tan^{-1} \left( \frac{\epsilon +1 }{60 \sigma \lambda} \right) \tag{9} \] となるので、\( (\epsilon +1) \ll 60 \sigma \lambda \)であれば、より具体的には\( (\epsilon +1) / 60 \sigma \lambda < 0.2 \)であればbが10°以下になるため、b=0とみなしても大きな誤差はありません。
そのため、数値距離pは \[ p_1 \simeq \frac{\pi r}{60 \sigma \lambda^2} \tag{10} \] と近似することができます。
さらに簡易的な表現であれば、実用単位に変換した以下の式(11)が利用しやすいと思います。 \[ p= 0.000583 \times \rho \times r_{km} \times f_{MHz}^{2} \tag{11} \]
式(11)と式(10)は全く同じもので、ρは大地抵抗率を表し、単位は[Ω⋅m]です。(補足:大地導電率σとの関係は\( \sigma = 1 / \rho \)で大地抵抗率は導電率の逆数になる。)
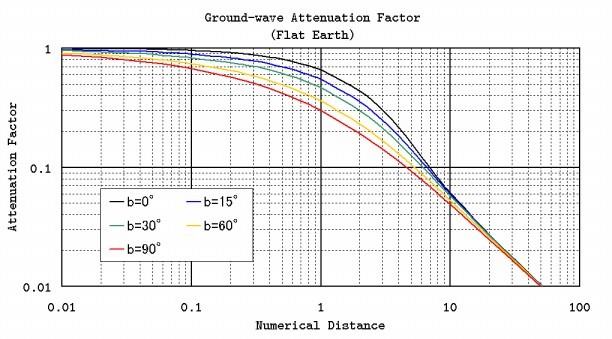
5.5 減衰関数のグラフ
グラフから値を求めるときに使用します。(クリックすると拡大します)
グラフの元となった数値表は別ページに分離してあります。必要な方は(付録)地表波減衰係数表をご覧ください。
5.6 減衰係数関数の近似式1
数値距離pと偏角bより、減衰係数Aを計算するための近似式はファン・デル・ポ-ル(B.Van der Pol ;1931)の式が有名です。ただし、偏角の値は5°以下でなければなりません。 \[ |A|= \frac{2+0.3p}{2+p+0.6p^2} \ \ , \ (b < 5^\circ) \tag{12} \]
数値シミュレーションの値と比較すると、最大でも14%以下の誤差に収まります。(p=12のときに最大誤差)
5.7 減衰係数関数の近似式2
任意の偏角bを式(12)を利用して計算したい場合には、Nortonによって修正項が付加された次式を用いることが出来ます。 \[ |A| = \frac{2+0.3p}{2+p+0.6p^2} - \sin b \sqrt{\frac{p}{2}} \ e^{-0.625p} \tag{13} \] 式(13)はbが大きいとき、最大で-40%ほどの誤差がでました。(p=2,b=75°時)
5.8 減衰係数関数の近似式3
最後に、Nortonが論文[9]の中で紹介している、近似式を挙げます。こちらの式はpの大小によって式を変えなければなりません。 \begin{eqnarray} |A| = \begin{cases} e^{-0.43p+0.01p^2} - M &, (p \leq 4.5) \\ \cfrac{1}{2p-3.7} - M &, (p \geq 4.5) \\ \end{cases} \tag{14} \end{eqnarray} ここでの修正項Mは先と同じ値で、 \[ M=\sin b \sqrt{\frac{p}{2}} \ e^{-0.625p} \tag{14-1} \] です。
b=0のときには、きわめて精度が良く、最大でも2%弱という驚異的誤差におさまります。bが大きいと若干の誤差が(max -20%)出てしまいますが、式(13)よりも十分に優秀です。
5.9 減衰関数の近似式4 (p>20)
もし数値距離pがきわめて大きくなり、20以上であるならば、bに無関係に \[ |A| \simeq \frac{1}{2p} \tag{15} \] と近似できます。
これは図3でpの大きい部分をみてもよく分かると思います。式(15)は、式(13),(14),(15)のように実験的な近似式ではなく、解析的な解なのでかなり精度は良いです。(証明は別途)
5.A 詳細な解析的な話
数値シミュレーションするときの、式(6)の展開式などは、別途紹介する予定です。
5.11 減衰係数表
図3のグラフの元になった式(6)の表は、個別ページに分離しました。
6 実際の計算例
6.1 計算諸元
放送局の諸元が以下であるとき、送信所から30[km]離れた地点での電界強度を求めよ。
- 送信周波数:1[MHz]
- 送信出力:100[kW]
- 送信アンテナ:0.53λ 垂直接地アンテナ
- 大地の比誘電率:10
- 大地の抵抗率:100[Ω⋅m]
6.2 基本電界強度の計算例
完全導体の平面大地上にある0.53波長の送信アンテナからの電界強度は、式(4)を利用して、 \begin{eqnarray} E &=& 396 \times \frac{\sqrt{P_{(kW)}}}{d_{(km)}} \\ &=& 396 \times \frac{\sqrt{100}}{30} = 132 \mathrm{[mV/m]} \tag{16-1} \end{eqnarray} となり、この132[mV/m]に減衰係数をかけた値が電界強度である。
6.3 数値距離の計算例
大地の抵抗率ρが100[Ω⋅m]であるので、導電率σはρの逆数であるから、 \[ \rho=\frac{1}{\sigma}=\frac{1}{100}=0.01 \mathrm{[S/m]} \tag{16-2} \]
これを元に、xを計算すると \begin{eqnarray} x &=& \frac{1.8\times 10^4 \sigma}{f_{MHz}}\\ &=& \frac{18000 \times 0.01}{1} &=& 180 \tag{16-3} \end{eqnarray}
xより、偏角bを求めると、 \begin{eqnarray} b &=& \tan^{-1} \left( \frac{\epsilon_r +1 }{x} \right) \\ &=& \tan^{-1} \left( \frac{10+1}{180} \right) \\ &=& \tan^{-1} (0.0611) \\ &\simeq& 0.0610 \mathrm{[rad]} \\ &=& 3.5^\circ \tag{16-4} \end{eqnarray} となり、b=3.5°なので、ほぼb=0とみなしてもよいことが分かる。
また、計算する前にtan-1の中が0.2以下であれば、最初からb=0とおいても問題ない。このことは、bが10°以下のときは、0で近似するということを意味している。
次に、波長を計算すると、 \[ \lambda = \frac{300}{f_{MHz}}=\frac{300}{1}= 300 \mathrm{[m]} \tag{16-5} \]
以上の計算結果を元に、数値距離を計算すると \begin{eqnarray} p&=& \frac{\pi}{x} \frac{r}{\lambda} \cos b \\ &=& \frac{3.141}{180} \times \frac{30000}{300} \times \cos (0) \\ &=& 0.0175 \times 100 \times 1 \\ &=& 1.745 \tag{16-6} \end{eqnarray}
もちろん、(16-6)だけでなく、次式で計算してもよい。 \begin{eqnarray} p&=& 0.000583 \times \rho \times r_{km} \times f_{MHz}^{2} \\ &=& 0.000583 \times 100 \times 30 \times 1^2 \\ &=& 1.749 \tag{16-7} \end{eqnarray}
6.4 減衰係数の計算例
式(16-6)または(16-7)の数値距離をNorton近似式(14)に代入して、減衰関数を求める。 \begin{eqnarray} |A| &=& e^{-0.43p+0.01p^2} \\ && \ \ \ - \sin b \sqrt{\frac{p}{2}} \ e^{-0.625p} \\ &=& e^{-0.750+0.030} -0 \\ &=& e^{-0.720} \\ &=& 0.487 \tag{16-8} \end{eqnarray}
以上で、減衰係数が求められました。約半分(48.7%)に電界強度が減衰することになるわけです。もちろん、図3を使ってグラフで求めても良いです。
最後に、完全導体上の電界強度に、減衰係数をかけると最終的な電界強度が計算できて、 \begin{eqnarray} E &=& E_0 |A| \\ &=& 132 \times 0.487 \\ &=& 64.3 \mathrm{[mV/m]} \tag{16-9} \end{eqnarray} となりました。皆さんも計算してみてください。
7.大地定数データ
表1 出典:文献[15]
| 大地の状態 | 比誘電率 | 導電率 |
|---|---|---|
| 海水 | 80 | 4.5 |
| 淡水 | 80 | 0.01 |
| 湿地 | 8 | 0.005 |
| 乾地 | 4 | 0.0001 |
| 都市 | 5 | 0.001 |
大元のデータがどこにあるのか分かりませんが、この辺でだいたいの感覚が掴めるかも。
表2 出典:文献[16]
| 大地の状態 | 比誘電率 | 導電率 |
|---|---|---|
| 山岳地帯 | 15 | 0.001 |
| 丘陵地帯 | 15 | 0.002 |
| 平野地帯 | 15 | 0.005 |
| 海上 | 80 | 5 |
表2は法律上のものです。
関東平野地域では、おおむね、比誘電率10、大地抵抗率を100~200Ω程度とすればよいかと思います。文献[17][18]では、関東平野の陸上伝搬定数を比誘電率10、大地抵抗率を100Ωとしていました。日本の大地抵抗率については(株)サンコーシヤ 日本の大地抵抗率地図を参照するとよいでしょう。
8.参考文献
- [1] 電波法施行規則第二条1項24号(平成29年8月29日総務省令第57号改正時版)
- [2] 国立天文台編,"理科年表",1998,丸善,pp893-911
- [3] 諏訪欣也,古谷恒雄,"空中線系及び電波伝搬",1971,啓学出版
- [4] 虫明康人,"アンテナ・電波伝搬",1961,コロナ社
- [5] K.A.Norton, "The Calculations of Ground-Wave Field Intensity Over a Finitely Conducting Spherical Earth", Proceeding of The IRE, vol.29 December 1941,pp.623-639
- [6] http://www.tbs.co.jp/radio/sales/cm/howmany.html
- [7] 満保正喜,長野勇,香川幸雄,深見哲男,"スポラディックE層を考慮した中波近距離夜間伝搬曲線",電子情報通信学会論文誌 B Vol.J69-B No.5 May 1986,pp.541-549
- [8] 放送局の開設の根本的基準第二条11項(平成19年3月9日総務省令第23号改正版)
- [9] K.A.Norton, "The propagation of radio waves over the surface of the earth and in the upper atmosphere Part1", Proc. IRE, vol. 24,Oct.1936,pp.1367-1387.
- [10] K.A.Norton, "The propagation of radio waves over the surface of the earth and in the upper atmosphere Part2" , Proc. IRE, vol. 25 Sept 1937. pp.1203-1236.
- [11] D.A.Hill,J.R.Wait"Ground wave attenuation function for a spherical earth with arbitary impedance",Radio Science,vol. 15,May.1980,pp.637-643.
- [12] 谷口慶治,"アンテナの電波伝搬",2006,共立出版.
- [13] 奥井重彦."電子通信工学のための特殊関数とその応用",1997,森北出版
- [14] Abramowitz and Stegun , "Handbook of Mathematical Functions"
- [15] 吉川忠久,"2陸技 1・2総通受験教室④ 無線工学B",1992,東京電機大学出版局.
- [16] 昭和三十五年郵政省告示第六百四十号(無線局免許手続き規則第七条第四項の規定に基づく放送区域等を計算による電界強度に基づいて定める場合における当該電界強度の算出方法)(昭和35年8月9日)
- [17] 河野徹,石原豊彦,"インピーダンス値が異なる陸海混合経路上の地表波伝搬",2005年電子情報通信学会総合大会論文集,C-1-31,pp.31.
- [18] 河野徹,石原豊彦,"Ground Wave Propagation over a Homogenous Impedance Surface and a Mixed-Path with Inhomogeneous Impedance Surfaces Including Tropospheric Ducting Effect",Proc. IEEE Antennas and Propagation Society International Symposium 2006,pp.4735-4738.