バイアスはダイオードを救えるのか?
1.はじめに
無線の黎明期から使われる鉱石ラジオの感度アップ手法 ― バイアス ―は、実際にどのような影響を与えるのでしょうか?
現在のゲルマ/鉱石ラジオでは、無電源がウリになっていることもあり、あまり盛んではなさそうです。何といっても、電源を付けるぐらいならば増幅器も付けてしまえるということに尽きるでしょう。
しかし、鉱石検波器しか無かった時代には、この方法が安定して高感度を得る手法であったようで、現代でもシリコンダイオードを利用するにはバイアスが欠かせません。
そこで、バイアスをかけたダイオード検波器がどのような特性を持つか論じていきたいと思います。
2.結論から先に
数式的な解析が主になってしまうため、先に、結論を書いてしまいます。
別な言い方をすれば、個々のダイオード固有値である $I_s$ を自由に設定できるということです。感度のコントロールはもちろん、入力インピーダンスの設定も可能。
鉱石(探り式)や ゲルマニウムダイオード (Ge Diode) 、あるいは ショットキーバリアダイオード (SBD: Schottky Barrier Diode) では効果が限定的で、素子がもつ Rs 特性の悪さ(内部抵抗成分)が足を引っ張り、あまりメリットが発揮できません。
むしろ、汎用の小信号スイッチングダイオード (Si Diode) にバイアスを掛けることで、既存の SBD を超える性能が引き出せます。
汎用 Si Diodeに、0.1~1μA 程度を流すと、鉱石/Ge/SBDに匹敵する感度が得られ、その直列抵抗成分の低さから、性能も楽に引き出せて汎用性も高いということです。
ただし、バイアスを掛け過ぎると感度が低下してしまいます。理由の一つは、ダイオードに電流を流しすぎると「ただの抵抗器」になってしまうからです。
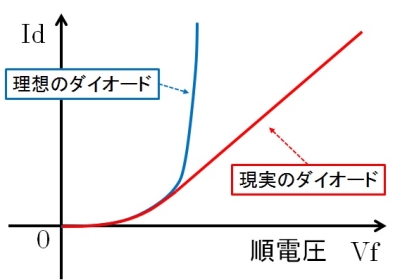
fig.1 理想ダイオードと現実の違い
理想のダイオードでは、どんなバイアス値でもよいのでしょうが、実際には電流が多くなるにつれて内部抵抗成分 Rs が支配的になり、V-I 特性が直線的になります。この直線領域に至るまでバイアスを過剰に掛けてしまうと、fig.2 の動作点 Q1 で動かす事になります。
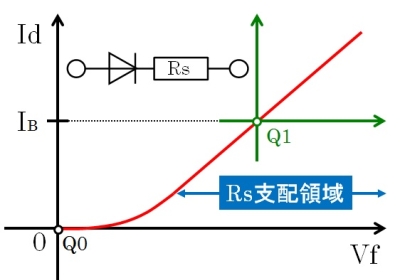
fig.2 過剰バイアス時のダイオード動作点
この Q1 付近ではグラフがほぼ直線ですので、微小信号に対しては単なる抵抗器としてしか動作していません。ほとんど検波動作を行っていないわけです。
そのため、過剰なバイアスは却って感度を落としてしまいます。
もう一つの問題点は、入力インピーダンス (Zi) の低下です。バイアス電流が大きいほど、無駄なRF電力の消費が発生します。このことで、微小信号領域での Zi が大きく下がってしまいます。
その値は 26mV/Bias が目安。もし 10μA ものバイアスを流すと、入力Zは 2.6kΩ まで低下し、同調回路の Q も 10 以下に大幅低下。結果として、高感度にし過ぎたために、微弱信号が検波できなくなるジレンマを抱えています。
これは元々高感度な Ge Di や Schottky Di であっても同じ性質を抱えています。。あまりに高感度すぎると、高インピーダンス検波動作には不向きということです。
\[ Z_i = \frac{V_T}{I_s+I_B} \simeq \frac{26\mathrm{mV}}{10\mathrm{\mu A}} = 2.6\mathrm{k\Omega} \]つまるところ、ダイオードの個体ごとに最適なバイアス値が存在するということです。
3.解析する回路モデル
バイアス電圧 $V_B$ をかけたダイオード検波器には、fig.3 のような回路を想定します。バイアスの掛け方にはいろいろ課題があるのですが、ひとまず置いておきましょう。
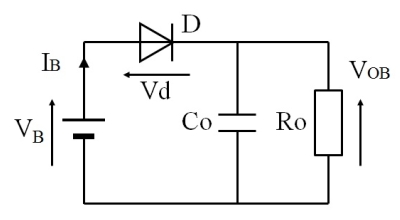
fig.3 バイアスをかけた検波回路
この回路では、RF未入力の状態でもバイアス電圧の一部が出力電圧 $V_{OB}$ として発生してしまいます。そのため、fig.4 のようにRF input $V_i$ に対する出力の増加分 $\Delta V_o$ を解析対象としなくてはなりません。
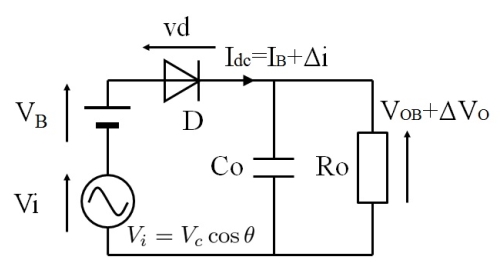
fig.4 RF入力時のバイアス検波回路
4.解析1(出力電圧)
まず $v_i = V_c cos \theta$ より、ダイオードの両端電圧 $v_d$ を求めると。
\[ v_d = V_c \cos \theta + V_B - V_o \tag{1} \]別ページで示した解を流用すると、出力電圧 $V_o$ の方程式は式(2)に帰着する。
\begin{eqnarray} V_o &=& V_T \ln \left[ f_0(V_c/V_T) \right] \\ && \ \ - V_T \ln \left[ 1 + \frac{I_{dc}}{I_s} \right] + V_B \tag{2} \end{eqnarray}式(2)から、BiasをかけてもRF入力によって生じる直流起電力の大きさは変わらないことが分かります。異なるのは、 $I_{dc}$ にBias電流成分が含まれている事、そしてBias電圧項が増えている部分です。
その、Bias電圧VBの方程式は式(3)で表すことができます。 \[ V_B=V_T \ln \left( 1 + \frac{I_B}{I_s} \right) + R_oI_B \tag{3} \]
そして求めたい出力電圧の増分ΔVoは、式(4)となります。 \[ \Delta V_o=V_o-V_{OB}=V_o-R_oI_B \tag{4} \]
簡単のために、起電力成分を $V_{d0}$ とおき、式(3)を式(2)に代入すると \begin{eqnarray} V_o &=& V_{d0}-V_T \ln \left( 1 + \frac{I_{dc}}{I_s} \right) \\ && \ \ \ +V_T \ln \left( 1 + \frac{I_B}{I_s} \right) +R_oI_B \tag{5} \end{eqnarray}
ここで、式(4)を利用して、 $\Delta V_o$ のみの形にすると、 \[ \Delta V_o=V_{d0}-V_T\left[\ln \left( 1 + \frac{I_{dc}}{I_s} \right) -\ln \left( 1 + \frac{I_B}{I_s} \right) \right] \] となり、さらにlogの中身をまとめて、 \[ \Delta V_o = V_{d0} - V_T \ln \left[\frac{I_s+I_{dc}}{I_s+I_B} \right] \tag{6} \] となる。
ここで、回路内の直流電流値 $I_{dc}$ は、Bias電流 $I_B$ とRF入力による増分 $\Delta I_{dc}$ の合計値であるので、 \[ I_{dc}=I_B+\Delta I_{dc} \tag{7} \] から、式(6)は \[ \Delta V_o=V_{d0}-V_T\ln \left( 1 + \frac{\Delta V_o}{(I_s+I_B)R_o} \right) \tag{8} \] の形でまとめることができます。
最後に式(8)を、無Biasの時の出力電圧式(9)と比較すれば、 \[ V_o=V_{d0}-V_T\ln \left( 1 + \frac{V_o}{I_s R_o} \right) \tag{9} \] ダイオードの電圧降下成分の項において、 $I_s$ であったものが、 $I_s + I_B$ に置き換わっていることが分かります。すなわち、ダイオードの電圧降下分がBias電流によって軽減されていることが見て取れます。
5.解析2(入力インピーダンス)
導出が少々複雑なため、途中計算は省略します(後日アップするかも?)。結果だけを書くと式(10)のようになります。 \[ Z_i = \frac{V_c}{2(I_s+ I_B+\Delta I_{dc})} \cdot \frac{f_0(V_c/V_T)}{f_1(V_c/V_T)} \tag{10} \]
要約すると、こちらも $I_s$ が $I_s+I_B$ となったのと同じようなRFインピーダンスを示しました。微小信号領域での入力Zは、ダイオード特性によって決定されてしまうのですが、Bias をかけることで、この辺を細かく制御できそうです。
一方で、 Bias電流 をガツンと流すと、かなり入力インピーダンスが落ちることも意味します。特に微小領域の入力インピーダンスは、負荷抵抗 $R_o$ にあまり関係せず、 \[ Z_i \simeq \frac{V_T}{I_s + I_B} \tag{11} \] となります。もし、 10μA も Bias を流してしまうと、 $V_T$ が26mV と仮定して、入力インピーダンスは 2.6kΩ までに低下する羽目になります。(この場合、大信号の方が逆に高インピーダンスになる逆転現象が起きる。)
この要因は、微小入力時に限り、ダイオードが抵抗に近い振る舞いをするからです。結果として同調回路の Q が激減し、出力も小さくなってしまいます。
単純に感度を上げたいという目的の場合は、Biasを流し過ぎないよう注意しなくてはなりません。
6.Biasのかけ方
実は意外に考えると面倒なのが、 Bias 電圧の与え方です。本当は Bias 「電流」を一発で決めてやりたいのですが、回路構成上、定電流電源を直列挿入できないため、並列挿入するか、定電圧電源を回路内のどこかに挿入してあげなくてはなりません。
下記の fig.5 の回路では、定電流源を使ってみたNGの例です。回路内のDC電流が定電流源で完全固定されてしまい、RFが入力されても出力電圧が変化できません。
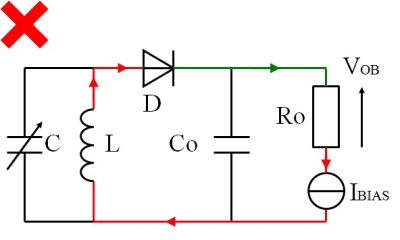
fig.5 定電流源で考えたNGの回路例1
定電流ソースを使うには、ダイオードと並列になるよう挿入してあげる必要があります(下記のfig.6)。残念なことに、負荷抵抗RoとダイオードDにBias電流が分流してしまうため、結局のところ電流値の調整が必要です。また、この回路では出力電圧に負のオフセットがかかります。(RF入力分の出力は正方向。)
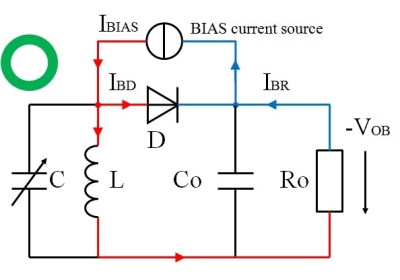
fig.6 定電流源で考えたBias回路例2
このとき、実際に作成する定電流源のインピーダンスは数MΩ以上は欲しいところで、負荷抵抗Roの十倍以上のインピーダンスが目安です。また、この回路は、定電圧源に置き換える事ができて、下のfig.7 と等価的な動きをします。
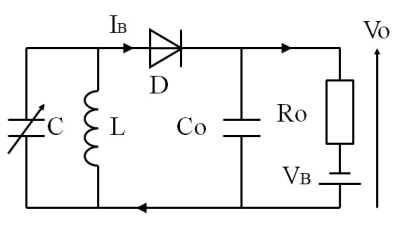
fig.7 定電圧源で考えたBias回路例1
そして、Bias電源を同調回路側に持ってくると、解析した回路モデルと等しくなります。ただし、実際にはLと直列に電源が入ってしまう構成であり、同調回路のQが低下しやすいので、いろいろ工夫をする必要もあります。そのため、fig.8 の回路は fig.7 の回路と比べると面倒で使いにくいでしょう。
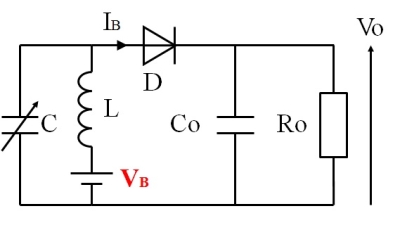
fig.8 定電圧源で考えたBias回路例2
これら、定電圧源でのBias回路は、なるべく内部抵抗を低くする必要があります。さもないと、動作点が入力信号に振り回されたり、場合によっては感度低下を招きます。
7.Biasの設計例
具体的な回路設計をしてみると、fig.9 のようになります。
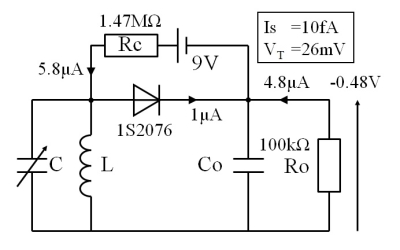
fig.9 定電流Biasの設計例
Siダイオード 1S2076 を使い、負荷抵抗 100kΩ でBiasを 1μA に設定した条件です。ダイオード特性は実測値を利用しました。9V電池を利用しているのは、なるべく内部インピーダンスを上げるためで、ここが泣き所と言えるでしょう。Rcは調整が必要な箇所ですので、可変抵抗器と組み合わせるのが良いと思います。
本末転倒かもしれませんが、トランジスタによるアクティブ定電流回路やカレントミラーなどを用いることもできます。この方が電源電圧が低くて済むものの、消費電力は却って増加してしまうでしょう。
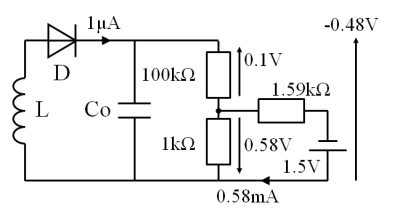
fig.10 定電圧Biasの設計例
次に、fig. 10 のような定電圧Biasの設計例です。fig.9 とほぼ同条件での算出ですが、分圧の都合上、負荷抵抗が 101kΩ と 1% だけ増えています。必要なBias電圧が低いため、1.5V の電池のみでも動かせるのは良い点でしょう。
泣き所は、消費電流の大きさです。fig.10 中の 1kΩ の値を増やすとよいのですが、ここはRF信号の入力による電圧変化がなるべく小さいことが求められるため、あまり増やすワケにはいきません。電流調整をするには、 1.59kΩ の抵抗を可変抵抗器にしておきます。
ではもう少し凝ってみましょうか、OPAMP定電圧回路を付加した fig.11 の回路です。
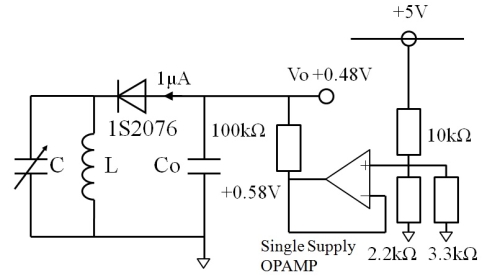
fig.11 定電圧Biasの設計例2
まぁ、やり過ぎというか… CMOS低消費電力タイプの単電源OPAMPを使えば多少は省エネにはなりますけどね。トータルで見ると、fig.10 の消費電力には勝てないような気がします。まぁジョークと思ってください。
8.簡易実験の結果
シリコンダイオード 1S2076 を使用して、 1μA のBiasを流した時の感度変化をメモしておきます。
fc=1MHz, fa=1kHz, m=30%, Ro=100kΩ, AF Trans (14kΩ/16Ω相当) + 汎用ヘッドホン使用 (ATH-SJ3) において、fig.10 と同等の回路で試験した結果です。ただ、入力電力は測定の都合で不正確のため、相対強度による比較です。
小信号になるほど、はっきりと聴覚上の差異が出ました。電子電圧計で検波出力が等しくなる SSG の出力差を測定した結果では感度が 4 - 5 dB 改善されました。ただ、ある一定以上の信号強度があるとその差は縮んでいき、改善が分からないか、あるいは 1dB 程度の改善にとどまりました。
例1)出力 3mV(rms) を得られるRF入力、Bias無し: -32dBm、 Bias有り: -37dBm例2)同一RFキャリア入力:-27dBm 、Bias無し出力: 10mV(rms)、Bias有り出力:11.5mV(rms)
このとき、 1S2076 のBias両端電圧は約 280mV で、想定の Is = 10fA よりも大きい値のようです。計算すると Is=21pA 相当ですから、以前の測定値と2000倍違いますね。バラツキや気温変化なども影響しているのでしょうか。