(付録4)
トランスの測定と理論
本ページは、ゲルマラジオとトランスの付録です。主にZHW-BT-OUT-101の測定に関する考え方と測定データについて補足します。
1. はじめに
トランス(変成器:Transformer)は、ゲルマラジオに限らず様々な場面で回路に利用されていますが、ここで扱うのは「音声周波数用トランス」に関しての測定や評価に関するものです。
電力用トランス(変圧器)や高周波トランス、伝送線路トランスなどでも共通する範囲は多いのですが、それぞれの用途に応じて重視するパラメータが異なるため、十把一絡げに扱うのは無理そうです。
このページを作成と実測にあたっては類似分類となる低周波トランスを測定評価されているAyumi's Lab.様を一つの指針として参考活用させていただきました。とても素晴らしいサイトです。
なお、このページはある程度電気回路知識がある方に、低周波トランスをどう理論的・実験的に扱うのがベターなのかという解説なので、初心者向きの解説ではありません。ごめんなさい。
2. トランス(変成器)に関する基礎理論
2.1 トランスとインピーダンス
トランスフォーマ、略してトランスは、信号用で使うときには変成器、強電分野では変圧器と呼ばれています。英語ではどちらも Transformer 。
トランスの基本構造は、透磁率の高いコアに線を巻きつけたものです。もっとも無線分野ではコアの無い空心トランスも沢山ありますけども。小学生の頃、クラスメイトのお父さんに無線工学を教わったとき、「トランスの巻数比で電圧の変換比が変わる」ことを知ったのですが、じゃぁ1回巻と2回巻きで1:4のトランスが出来るのではという素朴な発想があり、これは長らく疑問のままでした。
最初に習った内容は理想トランス (IT : Ideal Transformer) というモノだと言う事に気づいたのは随分後の話。少ない巻数だとインダクタンス(励磁リアクタンス)不足で低周波では使いものにならないんですね。
もう一つ、これは最近まではっきりと理解できていなかったのですが、トランスのインピーダンスという概念です。電力用トランスでは100V-6.3Vのように入出力電圧で記載されるので疑問がスルーされていましたが、信号用ではサンスイのSTトランスのように○○kΩと表示されてるので、いったい何を表しているのか?というのが疑問のままでした。
この表示はおそらく明確な基準では無いと思うのですが、「巻線比」「変圧比」を間接的に表現すると共に、トランスの「励磁リアクタンス」が定格インピーダンスにおける使用に耐えるという保証を示しているようです。
例えば、サンスイの ST-12 では 100kΩ という表記になっていますが、励磁リアクタンスは 1kHz 実測で +j292kΩ (46H)でした。すると、励磁リアクタンスが負荷抵抗と等しくなるのは 300Hz 前後になる勘定。このことから、「100kΩ(以下)のインピーダンスで使えば音声帯域 (300Hz-3kHz) をカバーしますよ」、という主張なのだと理解しています。
2.2 トランスの等価回路モデル
トランスを電気回路上で表現するためには、幾つかのモデルがあります。それぞれが別の考え方に立脚したものでどれを使うべきかは用途によって変わるものです。
大まかには、磁気回路に立脚したモデルと電気回路に立脚したモデルの二つがあり、その中間的なモデルを含め3種類が代表的なものと思います。
これらのモデルは見た目の回路図が一緒なのに中身がまるで違うので、大変まぎらわしいことに気をつけなくてはなりません。
2.2.1 磁気回路モデル
まず最初に紹介するのが磁気回路モデルです。回転機や変圧器などの電力機器ではこの表現が一般的です。
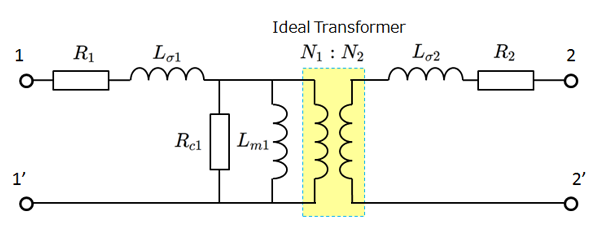
fig 2.1 トランス等価回路(磁気回路モデル)
回路定数の添字は1が1次側の値で、2が2次側の値です。 $R_1,R_2$ が巻線抵抗で銅損とも呼ばれます。そして $R_{c1}$ が鉄損(コア損失)を表しており、渦電流損やヒステリシス損を合わせたエネルギ損失分に相当します。
コイルから発生する磁束を分類したとき、両方のコイルに鎖交する共通磁束である主磁束 (Main flux) と、1次巻線のみあるいは2次巻線のみに鎖交する漏れ磁束 (Leakage flux) とに分けられます。
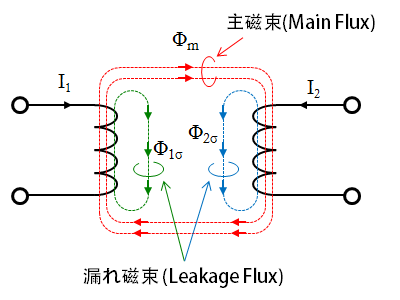
fig 2.2 トランスの磁束分類
このうち主磁束を発生させているインダクタンス成分である励磁インダクタンスを $L_m$ 、漏れ磁束の成分である漏れインダクタンスを $L_\sigma$ と表記しています。
一般的な低周波トランスにおいては、漏れインダクタンスが極めて小さく製作されていて、励磁インダクタンスの1/1000前後になると思われます。密結合トランスと呼ばれるときは、漏れインダクタンスが完全にゼロの仮想的なトランスという意味合いがあるので注意してください。
磁気回路に基くモデルは、鉄心(コア)を有するトランスを表現するのに適していて、コアの損失や磁気の状態をある程度織り込むことができます。
しかしながら、このモデルを有効に活用するにはコイルの巻数 $N_1,N_2$ という情報が必要で、既製品なら詳細データが無い限り公称変圧比で代用するしかなく、さほどのありがたみが感じられません。理想変圧比 $a$ (2次側換算比)は、式(1)で表現されます。 \[ a = \frac{N_1}{N_2} \tag{1} \] この換算比 $a$ を使って1次側に換算して理想変圧器を除去した等価回路図は、以下のようになります
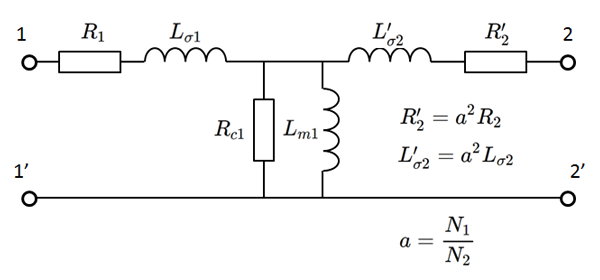
fig 2.3 磁気回路モデル(1次側換算)
2.2.2 電気回路モデル
次に、よく使われるのは電気回路モデルです。こちらは電気回路教科書の理論上のデバイスとして必ず紹介されるものです。
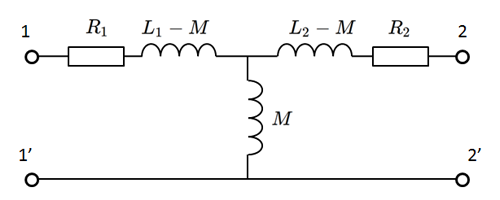
fig 2.4 トランス等価回路(電気回路モデル)
このモデルでは相互インダクタンス $M$ を通じて、トランスを純然たる電気回路素子として扱います。回路中に組み込んだときの電圧電流評価をするのにはとても良いものです。(シミュレーション向き)
なお $L_1$ は1次巻線の自己インダクタンス、 $L_2$ が2次巻線の自己インダクタンスです。
しかしながら、相互インダクタンス $M$ は、鉄心の磁気状態とは全く関係がなく、励磁インダクタンス $L_m$ とは異なる表現です。
鉄心入りトランスなどを精密に表現するには向きませんが、ゲルマラジオなどで使う、空心の高周波トランスを評価するにはこちらのモデルの方が役立ちそうです。
なお、この電気回路モデルは磁気回路モデルとの間で相互に変換可能であって、 \begin{eqnarray} L_1-M &\rightarrow& L_1-aM \\ L_2-M &\rightarrow& a^2L_2-aM \\ M &\rightarrow& aM \\ R_2 &\rightarrow& a^2 R_2 \end{eqnarray} と、値を書き換えれば、1次換算の形式(理想変成器を除去)で2つの等価回路が一致することになります。しかしながら、ここでも $a=N_1/N_2$ の巻線比が必要なので、未知のトランスを測定するには今ひとつだという印象を受けました。
2.2.3 修正電気回路モデル
こちらは、電気学会の教科書「電気回路論」で使われているモデルです。これはトランスの結合係数 $k$ を使い、かつ理想変圧比 $a$ を \[ a = \sqrt{\frac{L_1}{L_2}} \tag{2} \] と仮定することで、ほぼ磁気回路に近い扱いができるようにした電気回路モデルです。
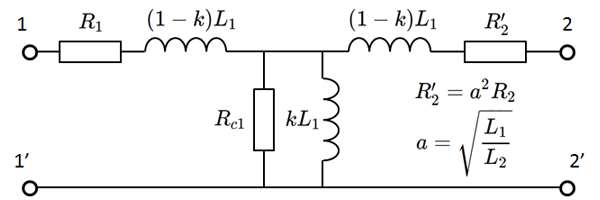
fig 2.5 トランス等価回路(電気回路モデル2)
強いていえば、電気回路モデルと磁気回路モデルの中間的な存在にあたるでしょう。
今回の測定に当たっては、巻線数 $N$ が不明であり、かつ、コアの損失や漏れインダクタンスもある程度考慮したいことから、電気学会モデルを採用することとしました。
本モデルを使うと1次側漏れインダクタンスと、2次側漏れインダクタンス(1次側換算値)が等しいと仮定することになります。(一般的なトランスでは磁気回路モデルを使ってもほとんど等しいと仮定できるので支障はなかったりします。)
計算や測定の手間が省けるの加え、一般的な密結合(k≒1)の低周波トランスではほとんど磁気回路モデルに一致することになるのでちょうど良さそうです。
結果として結合係数 $k$ も求めることになるので、結合係数値を入力する必要のあるSPICEシミュレーションにはもってこいだと思います。
3. ZHW-BT-OUT-101 の測定

トランス外観
1個500円の安価なゲルマラジオ/鉱石ラジオ用トランスですが、変成比が 200kΩ:8Ω という以外の特性は全く不明です。中間タップがあって 100kΩ:8Ω としても使えますがそこにはあまり興味が無かったりします。(販売ページ)
この手のパーツの販売は、いつ流通が途絶えるか分からないこともあり、今後、新しいトランスを入手した時に備えて、いろいろデータの取り方をまとめておこうと思った次第です。
そして、本編で紹介した結果がどのようにして得られたのか、皆さんの参考&自分用メモとして残そうとしたのがこの補足ページです。
製品としては「オートトランス」となっており、2次巻線と1次巻線が共通化されていますが、線番も全く違い、ただ1次巻線のGND側と2次のホット側端子を同一端子に半田付けしているだけだと判明したため、2次巻線を別端子にくっつけて普通のトランスに改造してあります。(改造しなくても測定自体は可能。ただ単に複数個のトランスを組合せて使えないだけです。)
3.1 直流抵抗の測定(DCR)
トランスの巻線抵抗である直流抵抗は、比較的容易に測定できるパラメータです。いろいろと信号周波数を変えることでトランスの詳しい定数を測定できるわけですが、その観点から見ると 0Hzでの周波数応答特性ということになるでしょう。
1次巻線の抵抗 $R_1$ は数百Ωあるので普通のテスタでも測定可能です。しかしながら、本トランスの2次巻線抵抗 $R_2$ は1Ω以下なので、高精度の測定器でないと厳しいものでした。結局、ミリオームの表示が信用できるLCRメータを使って測定しました。 (Agilent U1733C)
2次巻線は大変小さい値なので、1次側から間接的に測定する方法もあります。ただし、その場合でもLCRメータか測定ブリッジが欲しいところです。
| $R_1$ | 820.6Ω |
|---|---|
| $R_2$ | 267mΩ |
この巻線抵抗は銅線(Cu)の電気抵抗なので、温度によってそれなりの変化があります。室温での電気抵抗式としては以下の計算式があります。
\[ R = [1 + 0.00393 (T-20)] R_{20} \]$R$ が電気抵抗[Ω]、 $T$ が環境温度(℃)、 $R_{20}$ が 20℃ の時の電気抵抗です。
銅線抵抗の温度係数は0.393% [Ω/℃]なので5℃の温度変化があると2%の抵抗値の変化が見込まれます。温度計を横に置きながら測定すると惑わされずに済むと実感しました。(最初は計測のたびに値が変わるので、ちょっと迷いました。後で冷静に考えたら温度が原因と気付く。)
ちなみに、私が測定した時は T=19.6 のとき 813.2Ω、T=25.0 のとき 828.0Ωでしたので、20℃のときの $R_0$ は \[ R_{20} = \frac{828}{1 + 0.00393\times(25.0-20)} = 812.0Ω \] となりました。T=19.6から計算すると814.5Ωとなり、20℃で約 812 - 814Ω程度と推測されます。
一緒に購入した他のサンプルも測りましたが、ZHW-BT-OUT-101 はバラツキがやや大きいようで、$R_1$では以下のような測定結果でした。1次インダクタンスを規定値に合わせるよう巻数を増減しているのかもしれません。
| Sample | $R_1$ |
|---|---|
| No.1 | 785.5Ω |
| No.2 | 810.7Ω |
| No.3 | 812.2Ω |
| No.4 | 840.8Ω |
| No.5 | 792.2Ω |
| No.6 | 801.9Ω |
| No.7 | 842.8Ω |
注: No.2は全Sampleを測定したときの値で、最初に紹介した結果の820.6Ωと同一トランスです。温度による変動が要因です。
DCRの測定にあたっては、直流を流すことになるため、若干の直流偏磁の影響が残りますので注意してください。
DCR測定直後に、インダクタンスを測定したりすると、高めのインダクタンスを示します。例えば 38H 前後だったものが、42H前後に上昇し、測定中はどんどんと値が下降していくのが苦労した点でした。可能ならば、最初に交流測定をしておき、最後にDCR測定をしてパラメータを決定するのが良いと思います。LCRメータを2時間ぐらい連続測定すると落ち着きました。
消磁を試みましたが、大した効果が見られなかったので、上手に磁気を消すためには何かコツがあるのかもしれません。
3.2 2次開放(無負荷)測定
2次を開放した測定(無負荷測定)では、1次インダクタンス、浮遊容量、コア損失を測定することができます。
3.2.1 開放測定の原理
2次端子に何も接続しない開放状態のトランスは、1次インダクタンス $L_1$ と巻線に分布する浮遊容量 $C_s$によるLC並列共振回路として振舞います。
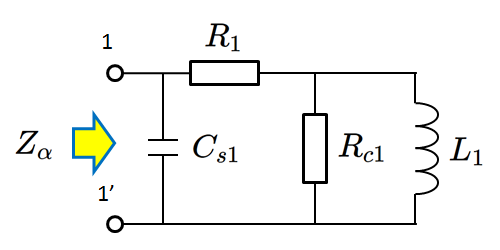
fig 3.1 2次側開放トランスの近似等価回路
1次側インダクタンス $L_1$ を測定するには、単一周波数のみのインピーダンスから算定する簡易な方法と、広帯域に渡って測定したインピーダンスプロットから算定する丁寧な方法が考えられます。
いずれの方法も、2次側端子には何もつながず開放状態(OPEN)にしておくのは変わりません。
特定周波数(例えば f=1kHz 固定)での測定は、LCRメータなどの精密な測定器が簡易に使えるのがとても良いのですが、浮遊容量 $C_s$ やコア損失 $R_c$ の影響が分離できないので、得られた値が信用できるかは測定対象によりけりです。
一方、広帯域で測定すれば全ての情報が得られるので、高級測定器がある前提ならこれ一択になるでしょう。ところが、汎用測定器(電子電圧計+低周波オシレータ)では非常に手間がかかるのが難点です。しかも位相情報が失われるため、コア損失のデータが相当不正確になります。
ですので、全帯域の測定後にLCRメータの測定精度を保証した上で精密値を得るのが良さそうに思えました。
3.2.2 測定回路と計算方法
次の図3.2が測定回路です。KENWOOD AG-203Dの発振周波数は伝統的なアナログダイヤル表示なので、汎用テスターの周波数カウンタ機能で測定しています。
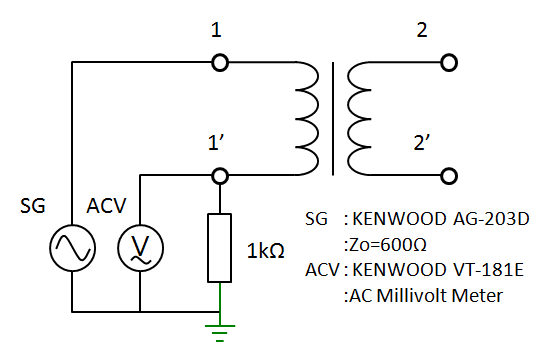
fig 3.2 測定回路
Vi=1V(rms) 一定の電圧をトランスに印加し、 R=1kΩ の抵抗に発生する電圧 Vm を電子電圧計で計測して電流値を得ます。このときトランスのインピーダンス(絶対値) $Z_\alpha$ は \[ |Z_\alpha| = R \left( \frac{|V_i|}{|V_m|}-1 \right) \] で計算できます。例えば1kHzでの例ですが、1kΩ両端電圧が4.10mVでしたので、 \[ |Z_\alpha| = 1.00 \rm{k \Omega}\times \left( \frac{1.00 \rm{V}}{4.10\rm{mV}}-1 \right) = 243 \rm{[k\Omega]} \] という測定結果となります。これを広帯域に渡って測定してプロットしていけばよいですが、大変面倒な作業でした。
3.2.3 2次開放測定結果と分析
測定結果の最終グラフが図3.3になります。
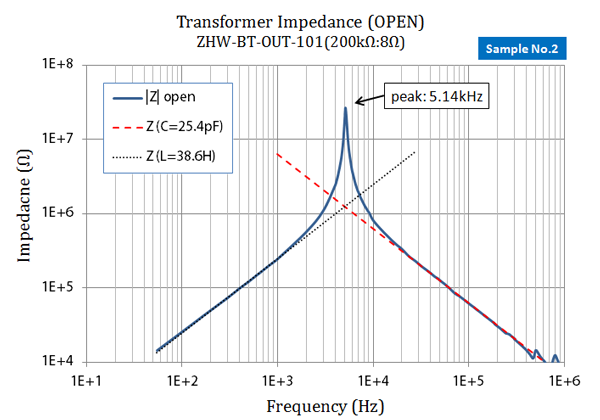
fig 3.3 トランスの1次側インピーダンス(2次開放)
低域では1次インダクタンス $L_1$ が優勢で、1kHz 程度までは浮遊容量 $C_s$ の影響はありませんでした。そこからは急激にZが上昇して5.14kHzで並列共振(26MΩ)したあと、20kHz 以上ではほとんど浮遊容量のみとなりました。
L1 は 100Hz - 1kHz の平均値、Csは 20kHz - 100kHz の平均値を採用して、L1=38.6H, Cs=25.4pFとしてあります。これらの共振周波数は 5.08kHz であるので、実測の共振周波数とほぼ一致していることが確認できました。
これらの結果を元に考えると、周波数固定式のLCRメータで測定するには、1kHzでL1を、100kHzでCsを測定すれば良いことになります。
しばらく経ってから LCRメータ Agilent U1733C で測定した値は、 Cs=22.65pF (100kHz)、 L1=40.2H (1kHz) でした。共振周波数の理論値は 5.28kHz になり先の測定値と少しズレています。
後で判明した事ですが、このトランスのL1は温度や磁場、直流を流したことなど測定条件により大きく値が変動します。最大で10%程度は変動すると見てよいでしょう。(実測では36Hから42H程度まで変動。)
少なくともLCRメータでの Cs 測定値は変動も小さく信用がおけますが、L1についてはだいたいが分かれば良いという程度にしておきます。また、その値も他サンプルも考慮し、かつキリがよい 40H を代表値としておきました。
元来、非線形な素子の性質が強い鉄心入りのトランスを線形電気回路として近似したモデルであるので、正確な表現は困難であると思われます。
3.3 1次インダクタンスの補正
前節の広帯域測定結果より、 f=1kHz で測定すると浮遊容量 $C_s$ が無視できて、$L_1$ が精度よく求められそうでした。しかしながら、コア損失 $R_{c1}$ があることで実際のインダクタンスよりも低く見えている可能性があります。
実際、過去にサンスイのST-12を測定したときにこのケースに遭遇し、ずいぶん迷った経験がありました。
そこで、LCRメータの測定値からコア損失とインダクタンスを分離するために、少々計算を行います。 \[ Z_\alpha(\mathrm{1kHz}) = R_\alpha + jX_\alpha =1.957 \mathrm{k\Omega} + j 252.5 \mathrm{k\Omega} \] がLCRメータで得られた複素インピーダンスの測定結果です。
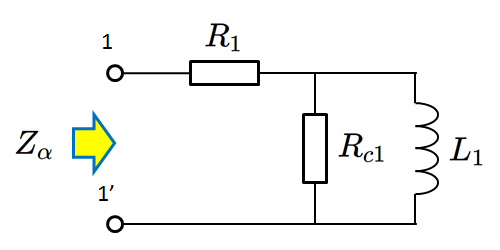
fig 3.4 2次側開放トランスの近似等価回路
既に1次巻線の直流抵抗値は測定済みで、 \[ R_1 = 820.6 \mathrm{\Omega} \] ですから、差分の$1.957-0.821=1.136\mathrm{k\Omega}$ がコア損失による増加分と想定されます。また1次巻線はAWG#40番線と極めて細いため、表皮効果を主とした周波数依存性は無視できると仮定します。
ここで浮遊容量Csさえ無視できれば、これらの数値からより正確なコア損失 ($R_{c1}$) と1次インダクタンス ($L_1$) を補正計算することができて、 \[ R_{c1} = (R_\alpha - R_1) + \frac{X_\alpha^2}{R_\alpha-R_1} \] \[ \omega L_1 = X_\alpha + \frac{(R_\alpha-R_1)^2}{X_\alpha} \] となります。(補足:ほぼ密結合のトランスである前提があるため、漏れインダクタンスの影響を無視することでコア損失を算出できる。)
実際に値を当てはめてみれば、 \[ R_{c1} = 1.136\mathrm{kΩ} + \frac{(252.5 \mathrm{k\Omega})^2}{1.136\mathrm{kΩ}} \approx 56.12 \mathrm{M\Omega} \] と非常に高い抵抗値になりました。これはかなりコア損失が少ないという意味になります。他サンプルでのQ値や、共振インピーダンスの測定結果(26MΩ)から見ても、妥当なオーダです。(補足: 26MΩの測定精度はかなり悪いハズです。1mV以下の小信号を無理やり測っているので、桁が合っていれば良いという程度と思ってください。)
コア損失 (Rc1) が極めて小さく低損失なことから、結局のところ補正式を使う意味も失われてしまって、1次インダクタンスL1は単純に、 \[ L_1 = \frac{X_\alpha}{2 \pi f} = \frac{252.5 \mathrm{k\Omega}}{6282} = 40.19 \mathrm{H} \] となります。
なお、補足になりますが、コア損失は理論的にみて周波数依存性があります。コアは高周波になるほどヒステリシス損(周波数に比例)と渦電流損(周波数の2乗に比例)が大きくなるのですが、結局、求めたいパラメータは音声周波数帯域内の大まかな代表値ですので、1kHzで測定した理由がここにあります。(今回のようなトランスの定電圧駆動条件だと、逆に高周波になるほど低損失に見えたりするので余計にややこしそうです。)
3.4 変圧比の測定
3.4.1 公称変圧比
変圧比 $a$ は、これもいろいろと測定方法が考えられるのですが、基本的には公称変圧比(定格) $a_n$ が一番の目安になります。(参考: n は nominal の意味)
$a_n$ の値はこの場合、インピーダンス比が200kΩ:8Ωなので、 \[ a_n = \sqrt{\frac{200\mathrm{k\Omega}}{8\mathrm{\Omega}}} = 158.11 \] と計算できます。しかしながら、今回はこれ自体がどこまで正しいのかどうかを判定したいのです。
3.4.2 入出力電圧比の測定
多少誤差がある手法ですが、単純に1次側印加電圧 V1 と2次側出力電圧 V2 を測定して比をとれば、まずは良いでしょう。
入力に1kHz 1V(rms)の電圧を印加して、2次側電圧を電子電圧計で測定すると、6.4mVでした。アナログメータなので気合を入れても6.4mVより微弱という不思議な表現になり、せいぜいが6.38mV程度であろうというのが読み取りの限界です。(1目盛り0.2mVの領域なのではっきり言えば無理しすぎ。)これを正しいとして計算してみると、 \[ a = \frac{1.00\mathrm{V}}{6.38\mathrm{mV}} = 156.74 \] となりました。あまりずれてはいませんが、少し変圧比が落ていますね。これで十分と言えば十分なのかもしれませんが。
このズレの原因は、変圧比が大きく微小電圧領域になってしまうため、測定器誤差がモロに影響することが挙げられます。それに、この手法は原理的に巻線抵抗などの影響を無視しているので、小さめな値になりやすいことも一つの要因でしょう。
念のため周波数を300-400Hz程度の低めにしてDMM(SANWA CD771)で測定してみると、さらに誤差が増えてしまいました。だいたい158から169程度までバラツキがあり、定格と大きく違わないと言う程度のあいまいな判定です。
3.4.3 既知の負荷抵抗による測定
次に、短絡したトランスの測定パラメータと、既知の負荷抵抗(RL)を2次端子にかまして、入力インピーダンスから間接的に求めてみたところ、かなり公称値に近く、再現性の高い結果が得られました (a=157.2から157.3)。が、これも検討してみると精度的に厳しそうで、偶然にこの値になった可能性が排除できませんでした。
なにぶん、1Ωの負荷抵抗が1次側から見ると25kΩに拡大されて見える極端な世界で、接触抵抗も含めてデリケートな取り扱いが必要なことを実感した次第です。
プロセスの詳細は3.5.2の流れにちょっと書いておきました。
3.4.4 負荷抵抗変化による測定
最終的に良好な結果が得られたのは、2次側に低抵抗の負荷抵抗をつけて微少量の変化を与え、1次側インピーダンス測定値の影響量から変圧比を求める方法です。このときインピーダンスの測定にあたっては、複素インピーダンスの実数成分を測定する必要があります。
具体的には、極めて小さい抵抗である0.1Ωと0.22Ωの酸化金属抵抗を負荷抵抗に用い、半田付けをしっかりして接触抵抗を排除するように注意。0.1Ωを負荷としたときの入力インピーダンス(実数成分)と、それに0.22Ωを加えた時の値を使って微分係数をとります。
理論的には精度を高めるために負荷抵抗をかなり小さく選ぶ必要があり、実験的にもそれが確認できました。測定の理論的な根拠については、ちょっと長いので4.1 補遺に書いてあります。
まずは 0.1Ω と 0.22Ω の抵抗値をLCRメータで測定しておきます。それぞれ 0.1011Ω, 0.2208Ω でした。よって合計値は 0.3218Ω となります。なお測定器のリード 抵抗分(約18mΩ)を除去済の値です。
そして、これらの負荷抵抗をつないだときの1次側インピーダンス(実数部)は、 0.1011Ω → 9.799kΩ 及び 0.3218Ω → 15.302kΩ でした。
これらの値から、変圧比aは \[ a = \sqrt{\frac{15.302\mathrm{k\Omega}-9.799\mathrm{k\Omega}}{0.3218\mathrm{\Omega}-0.1011\mathrm{\Omega}}} = 157.91 \] となり、3回の測定で157.91, 157.84, 157.90 と変動係数(CV)が0.021%と極めて良好な結果が得られています。
結論としては、公称値の158.1と相違ないというつまらない結果なのですが、特性不詳なトランスを測定するにはいろいろと苦労が必要なのだと思い知らされた1ヶ月でした。
3.5 2次短絡測定
2次端子を短絡させて測定することにより、漏れインダクタンスを測定することができます。無負荷測定の結果と合わせて、結合係数も求められます。
3.5.1 短絡法による測定
漏れインダクタンス $L_\sigma$ と結合係数は、密接な関係があり、2次側を短絡することで、測定をすることができます。
測定回路自体は、開放測定時と特に変わりません。
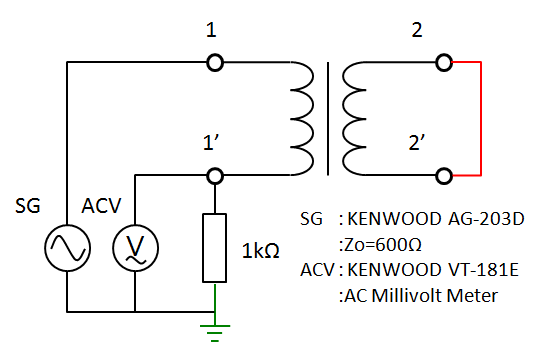
fig 3.5 短絡トランスの測定回路
2次端子の短絡時には以下のような等価回路になります。一般には、周波数を上げると励磁インダクタンス $L_{m1}$ がほとんど無視できるようになります。また、密結合のトランスなのでL型簡易等価回路とみなして、1次2次両方の漏れインダクタンスを片方に寄せて分析します。
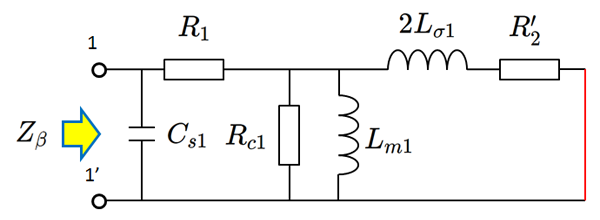
fig 3.6 2次短絡トランスの等価回路
周波数を上げると、浮遊容量 $Cs$ と漏れインダクタンス $L_\sigma$ で並列共振が生じて、インピーダンスプロットにピークが現れます。以下のグラフは実際の測定結果で、87.5kHzで共振が出ました。(5kHz - 10kHz あたりでグラフが凹んでいるのは、測定器のクセが原因でして、トランスに起因するものではありません。あしからず。)
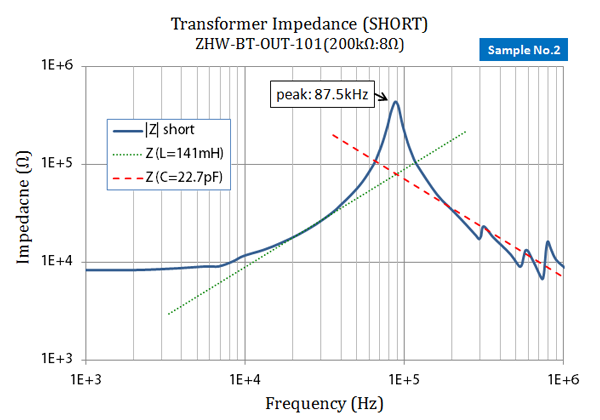
fig 3.7 トランスの1次側インピーダンス(2次短絡)
漏れインダクタンスを正確に求めるのは、なかなか面倒なのですが、グラフ上で6dB/Octの傾き、すなわち 周波数とインピーダンスが比例するあたりの帯域(要は $Z\sim \omega L$ になった 20kHz - 40kHz あたりの結果)から、 141mH 程度であると見積もる事ができました。
先に求めた Cs=22.7pF の結果と、今回の漏れインダクタンスの $2 L_{\sigma 1} = 141 \mathrm{mH}$ からすれば、 f=89.1kHz で共振するはずですので、実測の 87.5kHz とおおむね合致していると思います。
3.5.2 漏れインダクタンスの補正
より厳密さを目指し、1kHzで漏れインダクタンスをLCRメータで測定してから等価回路の補正をした結論では、 115mH という値が得られました。極端にはずれていませんが、ちょっと違っているのが気になるところです。
これは並列に入る励磁リアクタンスの影響を除外して、より純粋に漏れリアクタンスの影響を抽出した影響と考えています。除外せずに算定すると、1次側から142.2mHの短絡リアクタンスとして現れる計算結果になるので、この点からはよく一致しているようです。
以下に、補正を算定したプロセスをメモしておきます。方針としては、全てをいったんアドミタンスの並列素子表現に換算しておいて、励磁インダクタンス、コア損を差し引いた後、再びインピーダンス表現に変換するというものです。そのため、直並列変換をたびたび行います。
まず、1kHzにおける開放測定時の結果から励磁リアクタンス $X_{m1}$ が j252.5kΩ であることが分かってるので、ここではその逆数である、励磁サセプタンス $ B_{m1} $ を計算しておきます。 \[ j X_{m1} \simeq j \omega L_1 = +j 252.5\mathrm{k\Omega} \] の結果から、 \[ jB_{m1} = (jX_{m1})^{-1} = -j 3.961\mathrm{\mu S} \] が、最初に求めるべきアドミタンス成分です。同様にコア損(Gc1)は、 \[ G_{c1} = (56.12\mathrm{M\Omega})^{-1} = 17.82 \mathrm{nS} \] となります。
次にメイン測定である2次短絡時のLCRメータでの入力インピーダンス測定では、 \[ Z_{\beta1} = R_{\beta 1} +j X_{\beta 1} = 7.820\mathrm{k\Omega} + j 0.893 \mathrm{k\Omega} \] という結果が得られました。
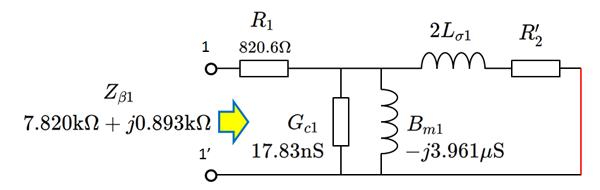
ここには、1次巻線抵抗 $R_1$ (820Ω)が含まれているので、それを除いた入力インピーダンスを $Z_{\beta}$ として、 \[ Z_{\beta} =(R_{\beta 1} -R_1) +j X_{\beta_1} = 6.560\mathrm{k\Omega} + j 0.893 \mathrm{k\Omega} \] となります。
この逆数である入力アドミタンス $Y_\beta$ は \[ Y_{\beta} =(Z_{\beta 1})^{-1} =G_\beta + jB_\beta = 149.7\mathrm{\mu S} - j20.38\mathrm{\mu S} \]
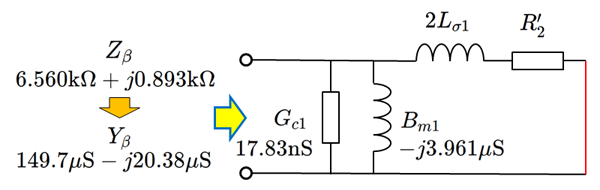
ここから、コア損( $ G_{c1} $ )と励磁インダクタンス ($ B_{m1} $)を差し引くと、漏れインダクタンスと2次巻線抵抗による合成アドミタンスのみが残る勘定です。これを $Y_{2L}$ とおけば、 \begin{eqnarray} Y_{2L} &=& G_L +j B_L \\ &=& (G_\beta -G_{c1}) +j (B_\beta-B_{m1}) \\ &=& 149.7\mathrm{\mu S} - j16.42\mathrm{\mu S} \end{eqnarray} が得られます。結局コア損(Gc1)が小さすぎて、実数部は無視してもよかったようですね。
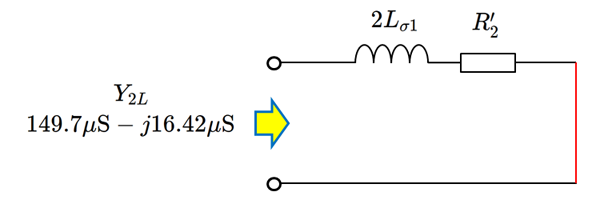
この $Y_{2L}$ の値は並列アドミタンス表現なので、元の直列インピーダンス表現に変換しておけば、実数部は、 \[ R_2^{\prime} = \frac{G_L}{G_L^2+B_L^2} = 6.602\mathrm{k\Omega} \] となって、2次抵抗の換算値である \[ a^2 R_2 = 158^2 \times 267\mathrm{mΩ} =6.665\mathrm{k\Omega} \] の値にほぼ等しいことが確認できます。それぞれは1%程度の違いしかないため、測定精度を考慮してもどちらの値を採用してもよいでしょう。ここでは6.665kΩの方を採用しておきます。
変圧比 $a$ はここから算出することもできて、DCRでの2次巻線抵抗 $R_2$ が 267mΩ であったことから、 \[ a = \sqrt{\frac{R_2^{\prime}}{R_2}}=\sqrt{\frac{6.602\mathrm{k\Omega}}{267\mathrm{m\Omega}}} = 157.25 \] という値も得られます。
そして、虚数部は全漏れリアクタンスに対応し \[ 2X_{\sigma1} = \frac{B_L^2}{G_L^2+B_L^2} = 724.3 \mathrm{\Omega} \] ですから、漏れインダクタンス(1kHz)は、 \[ 2L_{\sigma1} = \frac{724.3\mathrm{\Omega}}{2 \pi \times 10^3} = 115.3 \mathrm{mH} \] と算出できました。
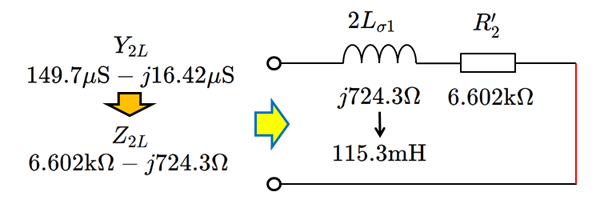
本サンプルでは、 115mH という結果でしたが、7サンプルでみると 10mH 程度のバラツキが見られました。ただ、1個だけ飛びぬけて高い(2倍程度)の製品もありましたので、製品の品質は安定していないようです。
最終的に、漏れインダクタンスを1次側と2次側に等分して(57.7mH)表現すれば、以下のような等価回路となります。
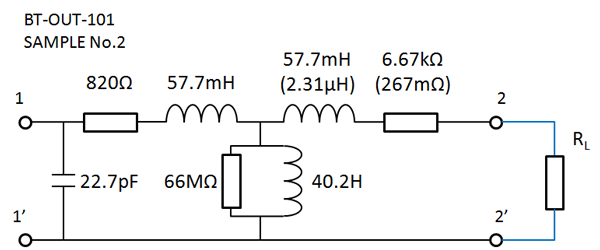
fig 3.8 トランスの最終パラメータ決定
3.5.3 結合係数の計算
結合係数 $k$ は、オープン・ショート法で直接求めてもよいのですが、せっかく漏れインダクタンスを正確に求めてみたので、あとは電気学会の定義から計算してみましょう。
\[ k = 1- \frac{L_{\sigma 1}}{L_1} =1 - \frac{57.7\mathrm{mH}}{40.2\mathrm{H}} = 0.9986 \]もし、一般的なオープン・ショート法で求めるならば、短絡インピーダンスの虚数部 j893Ω (=142mH) の値を使って \[ k = \sqrt{1-\frac{0.142\mathrm{H}}{40.2\mathrm{H}}} = 0.9982 \] となって、一見するとほぼ同じ値が得られたように見えますが、逆算で漏れインダクタンスを求めてみると、 \[ L_{\sigma 1} = 40.2 (1-0.9982) =72.4\mathrm{mH} \] と少し大きな値になり、こちらは励磁リアクタンス込みの合計値であることが想像できます。 (72.4×2=145mH ≒ 141mH)
以上から、結合係数は 0.9986 ≒ 0.999 程度と十分な結合度を持っていることが確認できました。おそらく比透磁率μが 1000 以上のコア材料を使っていると思います。
3.5.4 その他
本トランスは鉱石ラジオ用として悪くないものの、励磁インダクタンスが定格インピーダンスの200kΩで使用するには少し不足気味で、特に低音のロスが大きくなります。この点の改善については、ゲルマラジオとトランスの本編で実施していますので、興味のある方はこちらをご覧ください。
4 補遺
4.1 負荷抵抗変化による変圧比の推定根拠について
入力インピーダンスの実数部を $R_\beta$, 2次負荷抵抗と2次巻線抵抗の合計値 $R_2$ を1次側に換算した値を $ R_{2}^\prime $, 励磁リアクタンスを $ X_{m1} $ とし、かつ、結合度が高くて漏れインダクタンスを無視できるとします。 このときの入力インピーダンスの実部は、 \[ R_\beta = R_1 + \frac{ X_{m1}^2 R_{2}^\prime}{R_{2}^\prime+X_{m1}^2} \] となって、やや複雑です。
数式を簡単にするために、$ X_{m1}= A $, $ R_{2}^\prime = x$ と簡略表記にしておけば、 \[ R_\beta = R_1 + \frac{A^2 x}{x+A^2} \] になります。ここで、2次側の負荷純抵抗 $x$ が変化したときの微分係数をとってみると、 \[ \frac{d}{dx} R_\beta = \frac{A^4}{(x+A^2)^2} \] となってもっと複雑になってしまいます(あちゃー)。しかしながら、 $ A $ の値は 1kHz で 200kΩ超 、$x$ は20kΩ以下という条件を考慮すれば、 $A \gg x$ として、 \[ \frac{d}{dx} R_\beta \simeq 1 - \frac{2x}{A^2} \] と、まずは第一近似してしまいます。
ここで、負荷抵抗 $x$ が $A$ に比して十分に小さい値であることが保証できていること。つまり、0.2 - 0.3Ω程度の変化であれば $1 \gg 2x/A^2 $ が主張できるので、 \[ \frac{d}{dx} R_\beta \approx 1 \] と思い切った近似もできて、1次インピーダンス実数部の微小変化量 $\Delta R_\beta$ は、 \[ \Delta R_\beta = \Delta x = \Delta R_2^\prime \] と、2次側の抵抗変化がそのまま1次側の抵抗成分変化として現れることになります。
実際には、 \[ \Delta R_2^\prime = a^2 \Delta R_2 \] と、2次側の真の抵抗変化量に変圧比の2乗をかけた量になっているため、ここから変圧比を逆算すると \[ a = \sqrt{\frac{\Delta R_\beta}{\Delta R_2 } } \] となり、1次側のインピーダンス実数部の変化量を2次側の負荷純抵抗変化量で割って平方をとれば、変圧比が計算できることになります。
4.2 2次側の浮遊容量について
今回の測定では1次側の浮遊容量 $C_{s1}$ を測定しているのですが、2次側の浮遊容量 $C_{s2}$ は結果を出していません。
本当は大なり小なり存在するはずなのですが、本トランスにおいては明確にこの容量が算出できず、実質的に無視できているのではないかというのが私の推測です。
理論的には、無負荷測定時に|Z|グラフの落ち込みとして見えることを期待したのですが、明確な直列共振の兆候がなく、極めて小さい値か、他のパラメータに隠されて影響が出ていないのではないかと考えています。
1次側換算で 1pF 程度の影響があったと仮定したとき、2次側の実際の分布容量は変圧比の2乗をかけて \[ 158^2 \times 1 \times 10^{-12} = 25 \mathrm{nF} \] つまり、 0.025uF の容量が存在する計算なります。
さすがに、これは仮定に無理があると思われるので、本トランスの2次側分布容量はゼロとしてよいと考えています。